Resultate zu Rollkörper auf schiefer Ebene: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
(Die Seite wurde neu angelegt: „thumb|Schnittbild (free body diagram) 1. siehe Bild rechts 2. :<math>F_G\sin\beta-F_{HR}=\dot p_x=m\dot v_x</math> :<ma…“) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 9: | Zeile 9: | ||
3. |
3. |
||
:<math>\dot v = \frac {g}{k} \sin \beta</math> mit <math>k = 1 + \frac {J}{mr^2}</math> |
:<math>\dot v = \frac {g}{k} \sin \beta</math> mit <math>k = 1 + \frac {J}{mr^2}</math> |
||
4. ... |
|||
4. Der Weg über die [[Energiebilanz]] ist schneller, liefert aber keine Informationen zu den Zwangskräften ([[Normalkraft]] und [[Gleitreibung|Haftreibungskraft]]) |
|||
5. im Grenzfall 0 mm |
|||
:<math>\dot W_G+\dot W_{kin}+\dot W_{rot}=0, \quad W_G = m g h, \quad W_{kin} = \frac {m} {2} v^2, \quad W_{rot} = \frac {J}{2} \omega ^2</math> |
|||
:<math>mg\dot h+mv\dot v+J\omega\dot\omega=0</math> |
|||
Die Geschwindigkeit hängt mit der Änderungsrate der Höhe zusammen: <math> v = - \dot h \cdot sin\beta </math>. Mit Hilfe der Rollbedingung eliminiert man ω und seine Änderungsrate und erhält |
|||
:<math>-mg\sin\beta v + mv\dot v+ J \frac{v\dot v}{r^2} = 0 </math> |
|||
und daraus dann die gleiche Formel wie oben. |
|||
5. Die Kugel wird umso stärker beschleunigt, je kleiner der Faktor ''k'' ist, d.h. je weniger er von eins abweicht und je kleiner das Verhältnis des Massenträgheitsmoments zu Masse mal Quadrat des Abrollradius ''r'' ist. Mit dem Massenträgheitsmoment der Kugel J = 2/5 m R<sup>2</sup> und Kugelradius R wird |
|||
:<math> k = 1+\frac{2 R^2}{5 r^2}</math> |
|||
Die Kugel ist somit um so schneller, je weniger sich Abroll- und Kugelradius unterscheiden oder je kleiner die vom U-Profil gebildete "Spurweite" ist. Diese ist im Grenzfall 0 und beide Radien sind gleich. |
|||
'''[[Rollkörper auf schiefer Ebene|Aufgabe]]''' |
'''[[Rollkörper auf schiefer Ebene|Aufgabe]]''' |
||
Aktuelle Version vom 9. Mai 2012, 11:16 Uhr
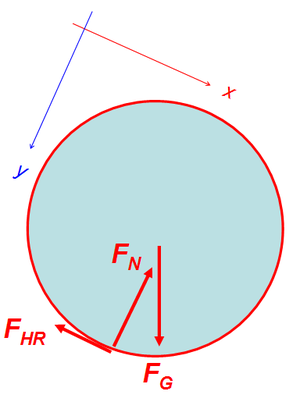
1. siehe Bild rechts
2.
- [math]F_G\sin\beta-F_{HR}=\dot p_x=m\dot v_x[/math]
- [math]F_G\cos\beta-F_N=\dot p_y=0[/math]
- [math]F_{HR}\cdot r=\dot L_z=J_z \dot \omega_z[/math]
3.
- [math]\dot v = \frac {g}{k} \sin \beta[/math] mit [math]k = 1 + \frac {J}{mr^2}[/math]
4. ...
5. im Grenzfall 0 mm