Reise um den Mond: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 16: | Zeile 16: | ||
==SD-Modell== |
==SD-Modell== |
||
[[Bild:Mondreise_SD.jpg|thumb|Das Systemdiagramm zur Berechnung der Mondreise]] |
|||
| ⚫ | Die Beschleunigung des Mondes ist gleich der Feldstärke der Erde am Ort des Mondes und umgekehrt. Die Beschleunigung des Satelliten ist zu jeder Zeit gleich der Überlagerung der Feldstärken von Erde und Mond. Diese rein kinematischen Lösung, erfordet für jeden der drei Körper vier Integratoren (stock, flow), also insgesamt zwölf Töpfe mit je einer Pipeline. Daneben müssen die sechs Komponenten der drei Abständsvektoren, sowie die zugehörigen Distanzen (Beträge der Abstandsvektoren) berechnet werden. |
||
| ⚫ | |||
| ⚫ | Die Beschleunigung des Mondes ist gleich der Feldstärke der Erde am Ort des Mondes und umgekehrt. Die Beschleunigung des Satelliten ist zu jeder Zeit gleich der Überlagerung der Feldstärken von Erde und Mond. Diese rein kinematischen Lösung, erfordet für jeden der drei Körper vier Integratoren (stock, flow), also insgesamt zwölf Töpfe mit je einer Pipeline. Daneben müssen die sechs Komponenten der drei Abständsvektoren, sowie die |
||
Anhand diese Modells kann man gut erkennen, wie weit sich die [[Physik der dynamischen Systeme]] von der Newtonsche Punkmechanik entfernt hat. Hier werden Felder superponiert, also Feldstärken vektoriell zu einer Gesamtwirkung addiert. Diese Gesamtwirkung ergibt dann die Beschleunigung des Systems, die über zwei Stufen aufzuintegrieren ist. Die Ideen der Bilanz, der konstitutiven Gesetze und der Rolle der Energie sind nur rudimentär vorhanden. |
|||
| ⚫ | |||
==Simulation== |
==Simulation== |
||
Version vom 14. August 2006, 18:19 Uhr
Handlung
Reise um den Mond (Autour de la Lune) ist ein Roman von Jules Verne aus dem Jahre 1870. Es handelt sich um die Fortsetzung des 1865 erschienen Werkes Von der Erde zum Mond.
Der Roman beschreibt die Abenteuer der drei Astronauten Barbicane, Nicholl und Ardan, die sich in einem Projektil befinden, das mithilfe einer Kanone gewaltiger Feuerkraft von der Erde aus in Richtung Mond abgeschossen wurde. Dabei landen sie, anders als geplant, nicht auf dem Mond, sondern umfliegen diesen und stürzen schließlich in den Pazifischen Ozean. Nach ihrer Rettung werden die drei Männer auf der Erde als Helden gefeiert.(Quelle:wikipedia)
Theorie
Wen die Frage interessiert, ob man mit einer 900 Fuss (pied du roi?) langen Kanone, die mit 400 000 Pfund Schiessbaumwolle geladen ist, die notwendige Geschwindigkeit von etwa 11 km/s (ohne die Bremswirkung der Luft) erreichen kann, soll mit einer thermodynamische Betrachtung die Ausströmgeschwindigkeit der heissen Gase abschätzen. Die mittlere Beschleunigungen, um auf einer Strecke von etwa 300 m zu eine Endgeschwindigkeit von 11.5 km/s zu erreichen, beträgt immerhin etwa 225 km/s2. Dies erzeugt im Bezugssystem des Projektils ein Trägheitsfeld, das etwa 22600 mal stärker ist als das Gravitationsfeld auf der Erdoberfläche.
Die Reise zum Mond ist ein Dreikörperproblem, von dem Jules Vernes weiss, dass "für diese Lösung die Integralrechnung aber noch nicht weit genug fortgeschritten ist". Da wir hier numerisch integrieren, muss uns diese Frage nicht weiter beschäftigen. Nimmt man das Gravitationsgesetz und das Aktionsprinzip von Newton, kürzt sich die Masse weg. Was übrig bleibt, ist reine Kinematik, also reine Geometrie:
Gravitatiosfeldstärke: [math]\vec g = - G \frac {m}{r^2} \frac {\vec r} {r}[/math]
Superpositionsprinzip: [math]\vec g_{tot} = \sum_{i} \vec g_i[/math]
freier Fall: [math]\vec g = \vec a[/math]
SD-Modell
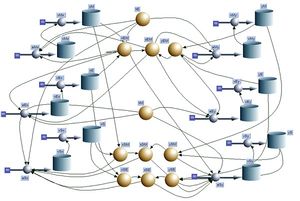
Die Beschleunigung des Mondes ist gleich der Feldstärke der Erde am Ort des Mondes und umgekehrt. Die Beschleunigung des Satelliten ist zu jeder Zeit gleich der Überlagerung der Feldstärken von Erde und Mond. Diese rein kinematischen Lösung, erfordet für jeden der drei Körper vier Integratoren (stock, flow), also insgesamt zwölf Töpfe mit je einer Pipeline. Daneben müssen die sechs Komponenten der drei Abständsvektoren, sowie die zugehörigen Distanzen (Beträge der Abstandsvektoren) berechnet werden.
Das Systemdiagramm zeigt auf der linken Seite die x-Komponente und auf der rechten Seite die y-Komponente für die drei Körper Monde, Erde und Satellit.
Anhand diese Modells kann man gut erkennen, wie weit sich die Physik der dynamischen Systeme von der Newtonsche Punkmechanik entfernt hat. Hier werden Felder superponiert, also Feldstärken vektoriell zu einer Gesamtwirkung addiert. Diese Gesamtwirkung ergibt dann die Beschleunigung des Systems, die über zwei Stufen aufzuintegrieren ist. Die Ideen der Bilanz, der konstitutiven Gesetze und der Rolle der Energie sind nur rudimentär vorhanden.