Ideales Gas

Modell

Das Modell des idealen Gases beschreibt den Zustand von stark verdünnten Stoffen; die Wechselwirkung zwischen den Teilchen dieses Stoffes sollte vernachlässigbar klein sein. Das Modell des idealen Gases ist auf gasförmige und gelöste Stoffe anwendbar.

thermische und mechanische Verbindung des idealen Gases

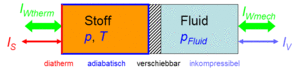
Der Zustand des idealen Gases kann auf zwei Arten verändert werden, durch heizen und kühlen oder durch komprimieren und entspannen. Um diese Prozesse kontrolliert ablaufen zu lassen, gehen wir von folgender Anordnung aus. Das Gas befinde sich in einem Zylinder, der mit einem Kolben verschlossen ist. Der Zylinderboden sei ideal wärmedurchlässig (diatherm), besitze aber selber keine Wärmekapazität. Die Zylinderwände und der Koblen sind absolut wärmeisoliert (adiabatisch). Der reibunsfrei verschiebbare Kolben schliesst das Gas hermetisch gegen eine Flüssigkeit ab, welche für den Druckaufbau verantwortlich ist. Bei Lösungen ist die Flüssigkeit gleichzeitig Lösungsmittel und der Kolben für das Lösungsmittel durchlässig, für den gelösten Stoff dagegen nicht. Einen dermassen selektiv durchlässigen Kolben nennt man semipermeabel.

Das Systeme Gas besitzt einen direkten thermischen und einen indirekten hydraulischen Kontakt zur Umgebung. Es kann somit mit der Umgebung Energie in Form von Wärme und Arbeit austauschen.

Bilanzen und Prozesse

Das ideal Gas besitzt zwei Verbindungen zur Aussenwelt (Portale oder Konnektoren), eine thermische und über das benachbarte Fluid eine hydraulische. Weil das Gas homogen ist und die Verbindungen ideal sind, wird innerhalb des Systems keine Entropie produziert. Folglich kann die Entropiebilanz und die Volumenbilanz in einfachster Form hingeschrieben werden

[math]\begin{matrix} I_S &=& \dot S \\ I_V &=& \dot V_{Fluid} = -\dot V \end{matrix}[/math]

Das ideale Gas kann als homogenes System mit zwei Verbingungen vier einfach zu realisierende Prozesse durchlaufen.

Prozess	Beschreibung	thermisches Portal	hydraulisches Portal
isochor	V =konst	aktiv	geschlossen
isobar	p =konst	aktiv	Kurzschluss
isentrop	S =konst	geschlossen	aktiv
isotherm	T =konst	Kurzschluss	aktiv

Beim isochoren und beim isentropen Prozess ist je ein Portal geschlossen, bei den beiden andern Prozesssen staht das nicht aktive Portal in enger Verbindung zur Umwelt.

konstitutive Gleichungen

Beim idealen Gas koppeln zwei Bilanzgleichungen über die beiden zugehörigen Potenziale. Im Gegensatz zum Massenpunt als dreifacher, aber entkoppelter Impulsspeicher und anders als beim starren Körper als dreifacher Drehimpulsspeicher, sind die beiden Speichergesetze nicht ganz einfach zu durchschauen.

Das erste Speichergesetz, die universelle Gasgleichung oder die thermische Zustandsgleichung des idealen Gases, verknüpft die drei diekt messbaren Grössen Druck, Volumen und Temperatur miteinander

[math]pV= nRT=mR_sT[/math]

Die erste Form basiert auf der Stoffmenge als natürliches Mass für die Menge eines Stoffes, die zweite nimmt die Masse als Hilfsgrösse, um die Menge des Soffes zu quantifizieren. R steht für die universelle Gaskonstante und R_s für die spezifische Gaskonstante, die für jeden Stoff einen andern Wert annimmt.

Das zweit Speichergesetz beschreibt die Entropie in Funktion des Volumens und der Temperatur

[math]S = S_0 + n (R ln \frac {V}{V_0} + \hat c_V ln \frac {T}{T_0}) = S_0 + m (R_s ln \frac {V}{V_0} + c_V ln \frac {T}{T_0})[/math]