Kettenlinie: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Version vom 1. Juni 2007, 07:24 Uhr

Eine Kette, die an den Enden befestigt wird und dazwischen herunterhängt, nimmt unabhängig von der Masse pro Länge eine bestimmte Form an. Diese sogenannte Kettenlinie, die eigentlich den Verlauf eines ideal biegsamen, linienförmigen Seils beschreibt, hängt von der Lage der Aufhängepunkte und der Länge der Kette ab, nicht jedoch von ihrer Masse pro Längeneinheit (μ).

Das Problem der Kettenlinie wurde von Gottfried Wilhelm Leibnitz, Christiaan Huygens und Johann Bernoulli im Jahr 1690 gelöst. Diese Lösung enthielt allerdings keine Herleitung. Johann Bernoulli wird erst in seinen Lektionen für L'Hospital expliziter. Galileo Galiei, der sich schon früher mit diesem Problem beschäftig hat, glaubte, dass die Kettenlinie eine Parabel sei. Eine Parabel ergäbe sich aber nur, wenn die Masse der Kette proportional zur Horizontaldistanz wäre.

klassische Herleitung

In der technischen Mechanik geht man Probleme dieser Art nach einem standardisierten Verfahren an

Freischneiden
Gleichgewichtsbedingungen formulieren
zusätzliche Annahmen und Gesetze beifügen

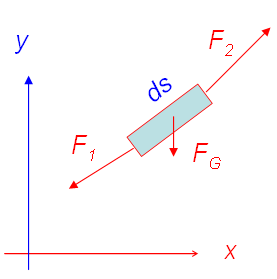
Das Schnittbild ist der nebenstehenden Skizze zu entnehmen. Die Bedingungen für das Gleichgewicht lauten

x-Richtung: [math]{-}F_{1x} + F_{2x} = 0[/math]

y-Richtung: [math]{-}F_{1y} + F_{2y} - F_G = 0[/math]

Die Gewichtskraft ist gleich Masse pro Länge mal Länge des Seilabschnittes mal Gravitationsfeldstärke

[math]F_G = \mu ds g [/math]

Nun führen wird für die Vertikalkomponente der Kräfte eine laufende Kraftvariable F_v(x) ein und verwenden für die konstant bleibende Horizontalkomponente den Parameter F_h. Damit wird die Gleichgewichtsbedingung in y-Richtung zu

[math]dF_v = \mu g ds = \mu g \sqrt{dx^2 + dy^2} = \mu g dx \sqrt{1 + \frac {dy^2} {dx^2}}[/math]

oder nach einer Division mit dx und der üblichen Bezeichnung für die Ableitung nach einer Ortsvariablen

[math]F_v' = \mu g dx \sqrt{1 + (y')^2}[/math]

Weil das Seil oder die Kette ideal biegsam ist, muss die Kraft auf einen beliebigen Querschnitt immer normal zur Schnittebene stehen. Dies führt zu folgender Zusatzbedingung

[math]\frac {F_v}{F_h} = \frac {dy}{dx} = y'[/math]

Leitet man diese Bedingung noch einmal nach der Ortsvariable x ab, folgt nach dem Einsetzen in die y-Gleichgewichtsbedingung die Differentialgleichung für die ideale Kette oder das ideale Seil

[math]y'' = \frac { \mu g }{F_h}\sqrt{1 + (y')^2} [/math]

@@ Zeile 1: / Zeile 1: @@
-Eine Kette, die an den Enden befestigt wird und dazwischen herunterhängt, nimmt unabhängig von der Masse pro Länge eine bestimmte Form an. Diese Kettenlinie hängt von der Lage der Aufhängepunkte und der Länge der Kette ab, nicht jedoch von ihrer [[Masse]] pro Längeneinheit (''&mu;'').
+Eine Kette, die an den Enden befestigt wird und dazwischen herunterhängt, nimmt unabhängig von der Masse pro Länge eine bestimmte Form an. Diese sogenannte Kettenlinie, die eigentlich den Verlauf eines ideal biegsamen, linienförmigen Seils beschreibt, hängt von der Lage der Aufhängepunkte und der Länge der Kette ab, nicht jedoch von ihrer [[Masse]] pro Längeneinheit (''&mu;'').
-Das Problem der Kettenlinie wurde von ''Gottfried Wilhelm Leibnitz'', ''Christiaan Huygens'' und ''Johann Bernoulli'' im Jahr 1690 gelöst. Diese Lösung enthielt allerdings keine Herleitung. Johann Bernoulli wird erst in seinen Lektionen für L'Hospital expliziter. ''Galileo Galiei'', der sich schon früher mit diesem Problem beschäftig hat, glaubte, dass die Kettenlinie eine Parabel sei. Eine Parabel ergäbe sich, wenn die Masse der Kette proportional zur Horizontaldistanz wäre.
+Das Problem der Kettenlinie wurde von ''Gottfried Wilhelm Leibnitz'', ''Christiaan Huygens'' und ''Johann Bernoulli'' im Jahr 1690 gelöst. Diese Lösung enthielt allerdings keine Herleitung. Johann Bernoulli wird erst in seinen Lektionen für L'Hospital expliziter. ''Galileo Galiei'', der sich schon früher mit diesem Problem beschäftig hat, glaubte, dass die Kettenlinie eine Parabel sei. Eine Parabel ergäbe sich aber nur, wenn die Masse der Kette proportional zur Horizontaldistanz wäre.
 ==klassische Herleitung==
@@ Zeile 11: / Zeile 11: @@
 Das Schnittbild ist der nebenstehenden Skizze zu entnehmen. Die Bedingungen für das Gleichgewicht lauten
-:''x''-Richtung: <math>{-}F_{1x} + -F_{2x} = 0</math>
+:''x''-Richtung: <math>{-}F_{1x} + F_{2x} = 0</math>
-:''y''-Richtung: <math>{-}F_{1y} + -F_{2y} - F_G = 0</math>
+:''y''-Richtung: <math>{-}F_{1y} + F_{2y} - F_G = 0</math>
-Die Gewichtskraft ist gleich Masse pro Länge ''&mu;'' mal Länge mal [[Gravitationsfeld|Gravitationsfeldstärke]]
+Die Gewichtskraft ist gleich Masse pro Länge mal Länge des Seilabschnittes mal [[Gravitationsfeld|Gravitationsfeldstärke]]
 :<math>F_G = \mu ds g </math>
-Nun führen wird die Vertikalkomponente der Kräfte eine laufende Kraftvariable ''F_V(x)'' ein und verwenden für die konstant bleibende Horizontalkomponente den Parameter F_H. Damit wird die Gleichgewichtsbedingung in ''y''-Richtung zu
+Nun führen wird für die Vertikalkomponente der Kräfte eine laufende Kraftvariable ''F<sub>v</sub>(''x'') ein und verwenden für die konstant bleibende Horizontalkomponente den Parameter F<sub>h</sub>. Damit wird die Gleichgewichtsbedingung in ''y''-Richtung zu
-:<math>dF_V = \mu g ds = \mu g \sqrt{dx^2 + dy^2} = \mu g dx \sqrt{1 + \frac {dy^2} {dx^2}}</math>
+:<math>dF_v = \mu g ds = \mu g \sqrt{dx^2 + dy^2} = \mu g dx \sqrt{1 + \frac {dy^2} {dx^2}}</math>
-oder nach einer Division mit ''dx'' und der üblichen Bezeichnung für eine Ableitung nach einer Ortsvariablen
+oder nach einer Division mit ''dx'' und der üblichen Bezeichnung für die Ableitung nach einer Ortsvariablen
-:<math>F_y' =  \mu g dx \sqrt{1 + (y')^2}</math>
+:<math>F_v' =  \mu g dx \sqrt{1 + (y')^2}</math>
-Eine weitere Forderung verlangt, dass die Schnittkraft auf eine ideale Kette oder ein ideales [[Seil]] immer normal zur Schnittebene steht. Dies führt zu folgender Zusatzbedingung
+Weil das [[Seil]] oder die Kette ideal biegsam ist, muss die Kraft auf einen beliebigen Querschnitt immer normal zur Schnittebene stehen. Dies führt zu folgender Zusatzbedingung
-:<math>\frac {F_V}{F_H} = \frac {dy}{dx} = y'</math>
+:<math>\frac {F_v}{F_h} = \frac {dy}{dx} = y'</math>
-Leitet man diese Nebenforderung einmal nach der Ortsvariable ''x'' ab, erhält man nach dem Einsetzen in die ''y''-Gleichgewichtsbedingung die Differentialgleichung für die ideale Kette oder das ideale Seil
+Leitet man diese Bedingung noch einmal nach der Ortsvariable ''x'' ab, folgt nach dem Einsetzen in die ''y''-Gleichgewichtsbedingung die Differentialgleichung für die ideale Kette oder das ideale Seil
-<math>y'' = \frac { \mu g }{F_H}\sqrt{1 + (y')^2} </math>
+:<math>y'' = \frac { \mu g }{F_h}\sqrt{1 + (y')^2} </math>
 ==systemdynamische Herleitung==