Kettenlinie

Eine Kette, die an den Enden befestigt wird und dazwischen herunterhängt, nimmt eine bestimmte Form an. Diese sogenannte Kettenlinie, die eigentlich den Verlauf eines ideal biegsamen, linienförmigen Seils beschreibt, hängt von der Lage der Aufhängepunkte und der Länge der Kette ab, nicht jedoch von ihrer Masse pro Längeneinheit (m*).

Das Problem der Kettenlinie wurde von Gottfried Wilhelm Leibnitz, Christiaan Huygens und Johann Bernoulli im Jahr 1690 gelöst. Diese Lösung enthielt allerdings keine Herleitung. Johann Bernoulli wird erst in seinen Lektionen für L'Hospital expliziter. Galileo Galiei, der sich schon früher mit diesem Problem beschäftig hat, glaubte, dass die Kettenlinie eine Parabel sei. Eine Parabel ergibt sich aber nur dann, wenn die Masse der Kette proportional zur Horizontaldistanz ist.

klassische Herleitung

In der technischen Mechanik geht man Probleme dieser Art nach einem standardisierten Verfahren an

Freischneiden
Gleichgewichtsbedingungen formulieren
zusätzliche Annahmen und Gesetze beifügen

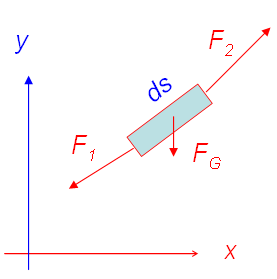
Das Schnittbild ist der nebenstehenden Skizze zu entnehmen. Die Bedingungen für das Gleichgewicht lauten

x-Richtung: [math]{-}F_{1x} + F_{2x} = 0[/math]

y-Richtung: [math]{-}F_{1y} + F_{2y} - F_G = 0[/math]

Die Gewichtskraft ist gleich Masse pro Länge m* mal Länge des Seilabschnittes ds mal Gravitationsfeldstärke g

[math]F_G = m^* ds g [/math]

Nun führen wird für die Vertikalkomponente der Kräfte eine laufende Kraftvariable F_v(x) ein und verwenden für die konstant bleibende Horizontalkomponente den Parameter F_h. Damit wird die Gleichgewichtsbedingung in y-Richtung zu

[math]dF_v = m^* g ds = m^* g \sqrt{dx^2 + dy^2} = m^* g dx \sqrt{1 + \frac {dy^2} {dx^2}}[/math]

oder nach einer Division mit dx und der üblichen Bezeichnung für die Ableitung nach einer Ortsvariablen

[math]\frac {dF_v}{dx} = F_v' = m* g \sqrt{1 + (y')^2}[/math]

Weil das Seil oder die Kette ideal biegsam ist, muss die Kraft auf einen beliebigen Querschnitt immer normal zur Schnittebene stehen. Dies führt zu folgender Zusatzbedingung

[math]\frac {F_v}{F_h} = \frac {dy}{dx} = y'[/math]

Leitet man diese Bedingung noch einmal nach der Ortsvariable x ab, folgt daraus nach dem Einsetzen in die y-Gleichgewichtsbedingung die Differentialgleichung für die Kettenlinie

[math]y'' = \frac { m^* g }{F_h}\sqrt{1 + (y')^2} [/math]

systemdynamische Herleitung

Durch das ideale Seil fliesst ein konstanter x-Impulsstrom gegen die x-Achse (I_px < 0). Zusätzlich fliesst der y-Impuls von beiden Befestungsstellen ins Seil hinein und geht entsprechend der Massenbelegung ans Gravitationsfeld weg. Für die Änderung der Stromstärke des y-Impulsstroms längs des Seils gilt

[math]dI_{py}=-m^*g ds = -\mu g \sqrt{dx^2 + dy^2}[/math]

oder nach der gleichen Umformung wie oben

[math]I_{py}'=-m^*g \sqrt{1+(y')^2}[/math]

Weil das Seil ideal weich bezüglich Biegung ist, kann es keinen Drehimpuls transportieren. Folglich dürfen keine Drehimpulsquellen auftreten. Die Forderung nach Quellenfreiheit führt zu einer zusätzlichen Forderung

[math]dy I_{px}-dx I_{py}=0[/math]

oder

[math]\frac {I_{py}}{I_{px}}=\frac {dy}{dx}=y'[/math]

Löst man nach der y-Komponente auf und leitet nochmals nach x ab, erhält man nach dem Einsetzen ebenfalls die Gleichung für die Kettenlinie

[math]y''= -\frac{ m^*g}{I_{px}}\sqrt{1+(y')^2}[/math]

Das Minuszeichen hat keine Bedeutung, da die Stromstärke des x-Impulses auch negativ ist.

Lösung

Die klassische und die systemdynamische Herleitung unterscheiden sich in zwei Punkten

In der klassischen Formulierung steht der Krafpfeil normal zum Querschnitt, damit keine Biegung auftritt. In der systemdynamischen Formulierung wird über die Biegefreiheit die Quellenfreiheit bezüglich der Grösse Drehimpuls postuliert.
In der klassischen Formulierung müssen Schnittebenen eingeführt werden, damit der Kraftbegriff überhaupt Sinn macht. Die systemdynamische Formulierung geht direkt vom Impuls als mengenartige Grösse aus.

Impulsströme

Wir setzen nun auf die klassische Schreibweise, übernehmen aber die Idee, dass jede Kraftkomponente die Stärke eines Impulsstromes bezüglich einer Referenzfläche beschreibt, aus der Physik der dynamischen Systeme. Wir beginnen mit der Gleichung, welche die Änderung der Impulsstromstärke längs der x-Achse beschreibt,

[math]dF_v=m^*gdx\sqrt{1+\frac {dy^2}{dx^2}}[/math]

dividieren sie durch die Stärke des x-Impulsstromes F_h und vereinfachen mittels der Substitution u = F_v / F_h = dy / dx

[math]du=\frac {m^*g}{F_h}dx\sqrt{1+(u')^2}=\frac{1}{k}dx\sqrt{1+(u')^2}[/math]

Separiert und integriert liefert diese Gleichung die Lösung

[math]arcsinh(u)=\frac{x}{k}+C=\frac{x-x_0}{k}[/math]

oder nach u aufgelöst

[math]u=\sinh(\frac{x-x_0}{k})[/math]

Setzt man die x-Werte bei der tiefsten Stelle des Seils gleich Null, gilt

[math]u=\sinh(\frac {x}{k})[/math]

Aufgelöst nach den Impulsstromstärken erhält man die Stärke des y-Impulsstromes in Funktion von x

[math]F_v = F_h \sinh (\frac {x}{k})[/math]

Die Stärken der Impulsströme beziehen sich auf eine Querschnittfläche, die in positive x-Richtung weist. Diese Orientierung kann mit einem Bezugspfeil markiert werden, der im Seil von links nach rechts verläuft. Die Stromstärke des x-Impulses (F_h) ist im ganzen Seil negativ, weil diese Komponente der Bewegungsmenge mit konstanter Stromstärke von rechts nach links fliesst.Im linken Ast ist die Stromstärke des y-Impulses (F_v) positiv, im rechten negativ. Die y-Komponente des Impulses strömt über beide Befestigungsstellen ins Seil hinein, um dann räumlich verteilt ans Gravitationsfeld weg zu fliessen.

Seilform

Ersetz man u durch u = F_v / F_h = dy / dx, integriert die Gleichung nochmals nach x und setzt den Ursprung des Koordinatensystems an die tiefste Stelle des idealen Seils oder der Kette, erhält man die Lösung der Kettenlinie in einfachster Form

[math]y = k \cosh\left(\frac{x}{k}\right)[/math]

Die Stärke des konstanten x-Impulsstromes F_h ist durch die Lage der Befestigungspunkte gegeben

[math]\frac {F_{v1}}{F_h} = \frac {y_1}{x_1}[/math] und [math]\frac {F_{v2}}{F_h} = \frac {y_2}{x_2}[/math]

Seillänge

Die Länge einer Linie in der x-y-Ebene berechnet sich aus der Summe über alle Teile

[math]L = \int_{s_1}^{s_2} ds = \int_{x_1}^{x_2} \sqrt{1+\left(\frac{dy}{dx}\right)^2}dx = \int_{x_1}^{x_2} \sqrt{1+(y')^2}dx [/math]

Setzt man für y die Funktion der Kettenlinie ein, ergibt sich eine Länge von

[math]L = \int_{x_1}^{x_2} \sqrt{1+\sinh\left(\frac {x}{k}\right)^2}dx = \int_{x_1}^{x_2} \cosh\left(\frac {x}{k}\right)dx = k\left( \sinh \left(\frac {x_2}{k}\right) - \sinh\left(\frac {x_1}{k}\right)\right)[/math]

Anwendungen

Drähte

An Masten aufgehängte Drähte nehmen die Form einer Kettenlinie an. Technisch wichtige Beispiele sind

Hochspannungsleitungen
unbelastetes Trag- oder Zugseil einer Luftseilbahn
Tragseil bei der Oberleitung der Eisenbahnen. Weil dieser Draht den Fahrdraht hält, bildet er keine exakte Kettenlinie

Bogen

Die an der Horizontalen gespiegelte Kettenlinie entspricht dem Verlauf eines selbsttragenden Bogens. In einem solchen Bogen wird kein Drehimpuls transportiert. Folglich steht er nicht unter Biegung. Sowohl der x- als auch der y-Impuls strömen so durch den Bogen, dass dieser unter reiner Druckbelastung steht. Der tiefere Grund dafür, dass die in der Kette vorhandene Zugspannung (Impulsstöme fliessen rückwärts) im Bogen in Druckspannung (Impulsströme fliessen vorwärts) übergeht, ist bei der Spiegelung selber zu suchen. Bildet man ein Objekt im Spiegel ab, ändert sich dessen Chiralität.