Reale Stoffe

In der Vorlesung zu Entropie und Enthalpie haben wir uns ein erstes Mal mit dem thermischen Verhalten realer Stoffe beschäftigt. Damals ging es ums Kühlen und Heizen bei konstantem Druck. In dieser Vorlesung untersuchen wir das Verhalten realer Stoffe unter Veränderung beider Potenzialgrössen (Temperatur und Druck). Wie beim idealen Gas stellen wir uns die Prozesse als ideal (reversibel) vor und lassen sie unter kontrollierten Bedingungen im Carnotor ablaufen. Dampfmaschinen können mit Hilfe des Rankine-Zyklus beschrieben werden. Für Wärmepumpen kann ein ähnlicher Zyklus gefunden werden.

Lernziele

In dieser Vorlesung lernen Sie

thermische Zustandsfläche

ideales Gas

Zustandsfläche des idealen Gases

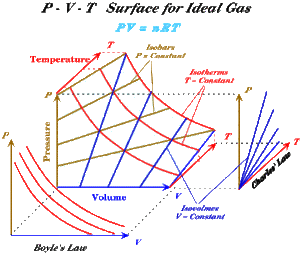
Trägt man alle Gleichgewichtszustände des idealen Gases in ein Druck-Temperatur-Volumen-Schaubild ein, erhält man eine Zustandsfläche, welche bei T = 0 entlang der Druck- und Temperaturachse verläuft und sich für bei höheren Temperaturen immer mehr von der Temperaturachse entfernt. Auf dieser Zustandsflächen lassen sich auf einfache Art und Weise drei verschiedene Kurvenscharen konstruieren

• die Isobaren: Schnittkurven der Zustandsfläche mit Ebenen die normal zur Druckachse stehen
• die Isochoren: Schnittkurven der Zustandsfläche mit Ebenen, die die normal zur Volumenachse stehen
• Isothermen: Schnittkurven der Zustandsfläche mit Ebenen, die normal zur Temperaturachse stehen

Projiziert man die Zustandsfläche auf die p-V-Ebene, stellen die Isothermen das Boylsche Gesetz dar. Eine Projektion auf die p-T-Ebene liefert die Kurvenschar der Isochoren (Gay-Lussac-Gesetz). Eine dritte Projektion auf die T-V-Ebene zeigt die Isobaren. Drei der vier möglichen Basisprozessen des idealen Gases lassen sich so direkt auf der Zustandsfläche einzeichnen. Einzig der isentrope Prozess ergibt eine Linie, die schief über die Zustandsfläche läuft.

Eine Zustandsänderung muss nicht weder isochor, isobar, isentrop noch isotherm verlaufen. Jede Abfolge von Gleichgewichtszuständen lässt sich auf der Zustandsfläche einzeichnen und auf eine der drei Koordinatenebenen projizieren. Die Darstellung im p-V-Diagramm nennt man auch Arbeitsdiagramm, weil die Fläche unter der Kurve der vom Gas in Form von Arbeit abgegebenen Energie entspricht. Im Arbeitsdiagramm erscheinen die Isobaren als horizontale und die Isochoren als vertikale Linien. Die Isothermen bilden beim idealen Gas eine Schar von Hyperbeln.

reale Stoffe

Zustandsfläche eines realen Stoffs

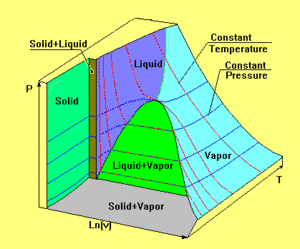
Reale Stoffe besitzen eine viel komplexere Zustandsfläche als das ideale Gas. In der nebenstehend abgebildeten Graphik ist die Zustandsfläche eines homogenen Stoffes dargestellt, wobei die drei Achsen nicht massstäblich aufgetragen sind. Durch Kanten getrennt zerfällt die Zustandsfläche in fünf Teile. Die grösste Teilfläche, die bei hoher Temperatur asymptotisch in die Zustandsfläche des idealen Gases übergeht, beschreibt alle Gleichgewichtszustände der gasförmigen und flüssigen Phase. Dazwischen erstreckt sich das Koexistenzgebiet flüssig-gasförmig. Entsprechend dem zur Verfügung stehenden Volumen liegt hier ein Teil des Stoffes im gasförmigen und der Rest im flüssigen Zustand vor. Dieses Stück der Zustandsfläche umschlingt die Volumenachse zylinderförmig. Die beiden andern Koexistenzgebiete (fest-gasförmig und fest-flüssig) sind ebenfalls zylinderförmig. Die gemeinsame Kante der drei Koexistenzgebiete heisst Tripellinie, weil bei diesem Druck und bei dieser Temperatur alle drei Phasen (fest, flüssig und gasfärmig) koexistieren. Die fünfte Teilfläche beschreibt den festen Zustand unter isotropem Druck. Weil ein Festkörper auch Schwerspannungen aufnehmen kann, lassen sich nicht alle möglichen Gleichgewichtszustände des festen Körpers in diesem Diagramm darstellen.

Der alltägliche Heizprozess verläuft längs einer Isobaren, weil unsere Atmosphäre den Druck bei etwa einem Bar stabilisiert. Liegt die Tripellinie höher als der atmosphärische Druck, wird der Stoff unter normalen Bedingungen nie flüssig. Dieses Verhalten ist beim Kohlenstoffdioxid bestens bekannt. Der Name Trockeneis leitet sich aus dem Umstand ab, dass gefrorenes CO₂ vom festen direkt in den gasförmigen Zustand übergeht (sublimiert), ohne vorher flüssig zu werden. Liegt der Druck über dem kritischen Punkt (Spitze des Koexistenzgebiets flüssig-gasförmig), wird die Unterscheidung zwischen flüssig und gasförmig hinfällig. Ein Gas, das bei so hohem Druck gekühlt wird, bildet nie einen Flüssigkeitssee.

Phasendiagramm

Phasendiagramm von UF₆

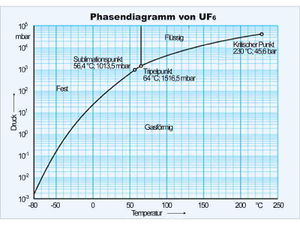
Projiziert man die Zustandsfläche auf die Druck-Temperatur-Ebene, erhält man das Zustands- oder Phasendiagramm. Im Phasendiagramm wird die Tripellinie zum Tripelpunkt und die drei Teilflächen, welche die Koexistenzgebiete darstellen, schrumpfen zu einer y-förmig verzweigten Linie. Diese Linien können nun als Graphen der Funktion p(T) gelesen werden. So ordnet die Dampfdruckkurve (rechter Ast des Y) jeder Temperatur zwischen dem Tripelpunkt und dem kritischen Punkt eindeutig einen Druck zu. Dieser Druck stellt sich bei einer gegebenen Temperatur automatisch ein, solange die flüssige und gasförmige Phase koexistieren. In den Koexistenzgebieten der Zustandsfläche müssen die Isobaren und die Isothermen zusammen fallen und parallel zur V-Achse verlaufen, damit die Projektion im Phasendiagramm einen einzigen Punkt ergibt.

Im nebenstehend abgebildeten Phasendiagramm von Uranhexafluorid