Zwei Bälle

Ein Basketball springt aus 2 m Höhe ohne weiteres Zutun aus dem Stand heraus höchstens 1,40 m hoch. Wird er aber auf einen Medizinball gelegt, wirkt dieser für den oberen Ball wie ein Trampolin. So kann der Basketball bis 6 m hoch steigen. (Quelle: Sat1/Clever)

Daten

• Medizinball klein
  • Masse 3 kg
  • Durchmesser 20 cm
• Medizinball gross
  • Masse 5 kg
  • Durchmesser 25 cm
• Basketball Grösse 7
  • Masse 0.63 kg
  • Durchmesser 23.5 cm
• Basketball Grösse 5
  • Masse 0.55 kg
  • Durchmesser 21.5 cm
• Basketball Grösse 3
  • Masse 0.33 kg
  • Durchmesser 18 cm

SD-Modell

Systemdiagramm mit Gleichungen

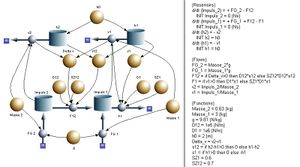
Jeder Ball wird als Masse mit zwei linearen Reibfedern (obere und untere Hälfte) modelliert. Eine Reibfeder besitzt zwei Federkonstanten, eine grosse für das Eindrücken und eine kleinere für den Rückhub. In unserem Fall entspricht das Verhältnis der beiden Federkonstanten dem Quotienten aus Rückprallhöhe und Fallhöhe. Dabei wird angenommen, dass dieses Verhältnis, das man Stosszahl nennt, unabhängig von der Fallhöhe ist. Der Luftwiderstand wird vernachlässigt.

Die Bezugsrichtung z zeige nach unten, damit das Gravitationsfeld Impuls zuführt und der Impulsinhalt des fallenden Balls zunimmt. Als Hilfsgrössen werden die Höhen h₁ und h₁ eingeführt. Die Höhe h₁ zeigt die Hubhöhe des Massenmittelpunkts des unteren Balls. Nullpunkt ist die Lage, in der dieser Ball den Boden ohne Verformung berührt. Die Höhe h₂ misst die Hubhöhe des Massenmittelpunkts des oberen Balls so, dass bei Null der obere auf den unteren zu liegen kommt. Mit dieser Wahl ist die dynamische Geschwindigkeit (Impulsinhalt durch Masse) gleich minus der Änderungsrate der zugehörigen Höhe. Als weitere Hilfsgrössen werden die Verformung des unter Teils des unteren Balls s₁ und die Verformung der beiden sich berührenden Hälften der Bälle s₁₂ eingeführt. Diese Wahl der Höhen und Verformungen erlaubt eine einfache Modellierung.

Die Federkonstante einer Serieschaltung von zwei Federn ist immer kleiner als die Federkonstanten der beiden Komponenten. Hier wird die Federkonstante der Hälfte des unteren Balls auf 1MN/m gesetzt. Für die sich berührenden Hälften der beiden Bälle wird eine zehn mal kleinere Federkonstante angenommen. Die Stoffzahl des Basketballs wird gemäss den oben gemachten Angaben auf 0.7 gesetzt.

Simulation

Parameterstudie

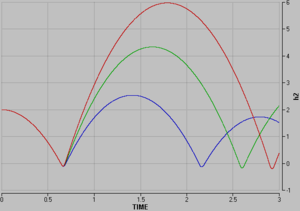
Die Graphik zeigt die Höhe des oberen Balls (Basketball Nr. 7) in Funktion der Zeit. Für den unteren Ball ist die Masse des des kleinen Medizinballs eingesetzt worden. Als Stosszahl für die obere Zone, die aus den sich berührenden Hälften der beiden Bälle besteht, ist - wie schon erwähnt - 0.7 eingesetzt worden. Die Stosszahl des Medizinballs ist in einem Batch-Run (CTRL-M) in zwei Schritten zwischen 0.2 und 0.7 variiert worden. Um die in der Fernsehsendung Clever erwähnte Höhe von 6 m bei einer anfänglichen Fallhöhe von 2 m zu erreichen, darf die Stosszahl des Medizinballs nicht zu klein sein. Der Medizinball verhält sich offensichtlich elastischer, wenn er von oben her noch gedrückt wird. Es stellt sich hier natürlich die Frage, wie weit dieses Problem durch ein Masse-Feder-Masse-Feder-Modell nachgebildet werden kann.