Magnetfeld und Induktivität

Elektrische Ladungen erzeugen das elektrische Feld (Feldstärke E gemessen in V/m oder N/C), elektrische Ströme das Magnetfeld (Feldstärke B gemessen in Tesla). Das elektrische Feld eines Kondensators (Kapazität C) sowie das Magnetfeld einer Spule (Induktivität L) speichern die vom Stromkreis zugeführte Energie.

Wird eine Kondensator geladen, fliesst Ladung von der einen Seite zu und verdrängt ebenso viel Ladung über den andern Anschluss. Die im damit erzeugten elektrischen Feld angesammelte Energie wächst quadratisch mit der Spannung und somit auch quadratisch mit der an einem beliebigen Punkt gemessenen Feldstärke.

Wickelt man einen Draht zu einer Spule, erzeugt der Strom im Innern der Spule ein starkes Magnetfeld. Dieses Magnetfeld kann mit Hilfe eines eingeschobenen Eisenkerns zusätzlich verstärkt werden. Die Stärke des Magnetfeldes wächst linear mit der Stärke des Stromes und die in diesem Feld gespeicherte Energie nimmt quadratisch mit der Stromstärke zu.

Lernziele

In dieser Vorlesung lernen Sie

• wie eine Induktivität wirkt
• wie viel Energie eine Spule bei gegebenem Strom speichert
• wie die Kapazität und die Induktivität den Strom bei angelegter Wechselspannung begrenzen
• wie der induktive und der kapazitive Blindwiderstand zu berechnen sind
• wie Schwingungsdauer (Periode), Frequenz und Kreisfrequenz zusammenhängen und bei einem LC-Kreis berechnet werden

Zudem wird die hydroelektrische Analogie vervollständigt.

Energiebilanz

Die Energie tritt in jedem Gebiet der Physik als Zweitgrösse auf, d.h. die Energie führt auf einer zweiten Ebene Buch über die ablaufenden Prozesse. Schauen wir uns diese Buchhaltung einmal etwas genauer an.

Die Energiebilanz bezüglich eines idealen Kondensators lautet

[math]UI=P=\dot W=CU\dot U[/math]

Die letzte Umformung folgt aus der Ableitung der im Kondensator gespeicherten Energie

[math]\dot W=\left(\frac{C}{2}U^2\right)^\circ=CU\dot U[/math]

Die Einheit der Kapazität, Farad, kann demnach auch als J / V² geschrieben werden.

Ladungen bauen das elektrische Feld, Ströme das Magnetfeld auf. Weil die von einem Kondensator gespeicherte Energie quadratisch mit der Ladung zunimmt, postulieren wir, dass die vom Magnetfeld einer Spule gespeicherte Energie quadratisch mit der Stärke des durchfliessenden Stromes anwächst.

[math]W=\frac{L}{2}I^2[/math]

L steht für Induktivität.Die Induktivität wird in Henry (H) gemessen (1 H = 1 J/A²). Die Division durch zwei übernehmen wir von der Kapazität.

Leitet man diese Energie-Strom-Beziehung nach der Zeit ab, folgt

[math]\dot W=\left(\frac{L}{2}I^2\right)^\circ=LI\dot I[/math]

Die Änderungsrate der Energie muss gleich der vom elektrischen Strom freigesetzte Leistung (Spannung mal Stromstärke) sein

[math]LI\dot I=\dot W=P=UI[/math]

Vergleicht man den Term ganz links mit dem Ausdruck ganz rechts, erhält man das konstitutive Gesetz der Induktivität: die Spannung über der Spule ist gleich Induktivität mal Änderungsrate der Stromstärke

[math]U=L\dot I[/math]

Eine induktive Spannung tritt demnach nur auf, wenn der Strom seine Stärke ändert. Nimmt man eine supraleitende Spule, deren Drähte dem Strom keinen Widerstand entgegen setzen, entspricht die gemessene Spannung immer der Änderungsrate des Stromes. Nimmt der Strom zu, sind Strom und Spannung gleich gerichtet. Bildlich gesprochen fliesst dann der Strom den Berg hinunter und setzt die Energie frei, die zum Aufbau des Magnetfeldes notwendig ist. Nimmt der Betrag des Stromes ab, sind Strom und Spannung wie bei einer Spannungsquelle gegeneinander gerichtet. Der Strom übernimmt dann die Energie, die das schwächer werdende Magnetfeld abgibt.

drei Elemente

Unser Baukasten enthält nun drei lineare Elemente. Das eine, der Widerstand, dissipiert Energie, die beiden andern, die Kapazität und die Induktivität wirken als Energiespeicher.

	Widerstand	Kapazität	Induktivität
konstitutives Gesetz	[math]U=RI[/math]	[math]\dot U=\frac{1}{C}I[/math]	[math]U=L\dot I[/math]
Einheit	[R] = Ohm (Ω)	[C] = Farad (F)	[L] = Henry (H)
Serieschaltung	direkte Addition	reziproke Addition	direkte Addition
Parallelschaltung	reziproke Addition	direkte Addition	reziproke Addition
Energie	[math]P_{diss}=RI^2=\frac{U^2}{R}[/math]	[math]W=\frac{C}{2}U^2[/math]	[math]W=\frac{L}{2}I^2[/math]

hydroelektrische Analogie

Nun, da die drei Elemente Widerstand, Kapazität und Induktivität auch in der Elektrodynamik bekannt sind, wollen wir die Analogie mit der Hydrodynamik nochmals rekapitulieren

Element	Hydro	Einheit	Elektro	Einheit
Menge	Volumen	m3	elektrische Ladung	Coulomb (C)
Strom	Volumenstrom IV	m3/s	elektrischer Strom I	Ampère (A)
Potenzial	Druck p	Pascal (Pa)	elektrisches Potenzial φ	Volt (1 V = 1 J/C = 1 W/A)
Energiestrom	[math]I_W=pI_V[/math]	1 Watt = 1 Pa m3/s	[math]I_W=\varphi I[/math]	1 Watt = 1 V A
Prozessleistung	[math]P=\Delta p I_V[/math]	1 Watt = 1 Pa m3/s	[math]P=U I[/math]	1 Watt = 1 V A
Widerstand	[math]R_V=\frac{\Delta p}{I_V}[/math]	Pas / m3	[math]R=\frac{U}{I}[/math]	1 Ohm = 1 V / A (Ω)
Kapazität	[math]C_V=\frac{\Delta V}{\Delta p}[/math]	m3/Pa	[math]C=\frac{Q}{U}[/math]	1 Farad = 1 C / V (F)
Induktivität	[math]L_V=\frac{\Delta p}{\dot I_V}[/math]	Pas2 / m3	[math]L=\frac{U}{\dot I}[/math]	1 Henry = 1 Vs / A (H)

Aus dieser Analogie folgt die Formel für die dissipierte Leistung

[math]P=R_V I_V^2 = RI^2[/math]

die kapazitive Energie

[math]W_C=\frac{C_V}{2}(\Delta p)^2=\frac{C}{2}U^2[/math]

sowie der induktiven Energie

[math]W_L=\frac{L_V}{2}I_V^2=\frac{L}{2}I^2[/math]

Trotz der schönen Symmetrie sollte man die Unterschiede nicht vergessen

• der Volumenstrom hat mit der Bewegung eines Stoffes zu tun, bei einem elektrischen Strom ist dagegen keine Bewegung nachweisbar
• Volumenströme koppeln über die Massenströme ans Gravitationsfeld
• Volumenströme können turbulent werden
• an engen Stellen tritt ein zusätzlicher Druckabfall auf
• elektrische Ströme fliessen nur in Kreisen, Volumen kann hingegen auch gespeichert werden

Blindwiderstand

induktiv

Strom und Spannung bei einer Spule

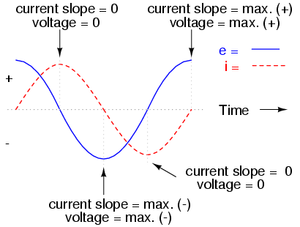
In einem Gedankenexperiment stellen wir uns vor, dass ein rein induktives Element, eine Wicklung aus supraleitendem Draht, an eine Steckdose angeschlossen wird. Die Steckdose erzeugt eine Wechselspannung mit einer Amplitude von 325 V

[math]U=U_0 \cos(\omega t)[/math]

Eigentlich müsste nun ein beliebig starker Strom durch den Draht fliessen, weil dieser keinen Widerstand aufweist. Setzt man aber die Formel für die Wechselspannung ins konstitutive Gesetz der Induktivität (Spannung ist gleich Induktivität mal Änderungsrate des Stromes) ein und löst nach der Änderungsrate des Stromes auf, folgt

[math]\dot I=\frac{U}{L}=\frac{U_0}{L}\cos(\omega t)[/math]

Eine Integration über die Zeit liefert

[math]I=\frac{U_0}{\omega L}\sin(\omega t)=I_0\sin(\omega t)[/math]

Obwohl das induktive Element keinen Widerstand aufweist, wird der Strom nicht unendlich gross. Die Amplitude der Stromstärke ist um so kleiner, je höher die Frequenz und je grösser die Induktivität ist. Das Maximum des Stromes läuft dem Spannungsmaximum um eine Viertelperiode nach.

Den Quotienten aus Spannungs- und Stromamplitude nennt man induktiven Blindwiderstand

[math]X_L=\frac{U_0}{I_0}=\omega L[/math]

Leistung bei einer Spule

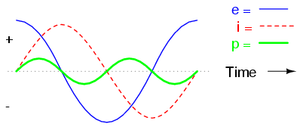
Der Blindwiderstand wird analog zum gewöhnlichen Widerstand definiert. Diese Definition berücksichtigt aber nur das Verhältnis der Amplituden. Die Phasenverschiebung muss separat beschrieben werden (entweder mit Hilfe eines Zeigerdiagramms oder einer komplexen Zahl). Jede Induktivität, die in Serie in den Stromkreis eingebaut wird, begrenzt die Stärke des durchfliessenden Stromes. Solche Drosselspulen findet man im Sockel jeder Leuchtstofflampe.

Der Widerstand heisst blind, weil keine Energie dissipiert wird: im Mittel fliesst gleich viel Leistung an die Steckdose zurück wie von dort bezogen wird

[math]P=UI=U_0 I_0 cos(\omega t)sin(\omega t)=\frac{U_0 I_0}{2}sin(2\omega t)[/math]

In einer Induktivität läuft die Spannung dem Strom um eine Viertelperiode voraus. Die Spannung muss zuerst aufgebaut werden, damit sich der durch das Magnetfeld träg gemachte Strom in Bewegung setzt.

kapazitiv

Strom und Spannung bei einem Kondensator

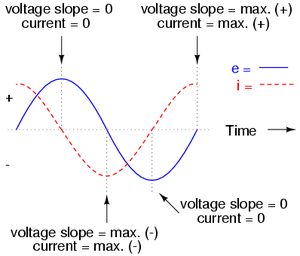
Verbindet man einen Kondensator mit einer Gleichspannungsquelle, fliesst solange ein durch die immer vorhandenen Widerstände begrenzter Strom, bis der Kondensator geladen ist. Dann passiert gar nichts mehr. Schliesst man eine reine Kapazität an die Steckdose an, darf man so nicht argumentieren. Dazu berechnen wir die Änderungsrate der Spannung

[math]\dot U=-U_0\omega\sin(\omega t)[/math]

und bestimmen mit Hilfe des konstitutiven Gesetzes (Stromstärke gleich Kapazität mal Änderungsrate der Spannung) die Stromstärke

[math]I=C\dot U=-U_0\omega C\sin(\omega t)=-I_0\sin(\omega t)[/math]

Im Wechselstromkrreis wirkt die Kapazität nicht wie eine Schranke. Der "durchfliessende" Strom wird jedoch leistungsfrei begrenzt. Bildet man nun den Quotienten aus Spannungs- und Stromamplitude, erhält man den so genannten Blindwiderstand

[math]X_C=\frac{U_0}{I_0}=\frac{1}{\omega C}[/math]

Der durch einen Kondensator fliessende Strom wird bei gegebener Spannung um so grösser, je höher die Frequenz und je grösser die Kapazität sind. Die Kapazität bezieht wie die Induktivität die Energie nur leihweise und schickt sie 100 mal die Sekunde ans Netz zurück.

In einer Kapazität hinkt die Spannung dem Strom um eine Viertelperiode hinter her. Der Strom muss zuerst zufliessen, bevor sich in der Kapazität eine Spannung aufgebaut hat.

Schwingkreis

Schwingkreis

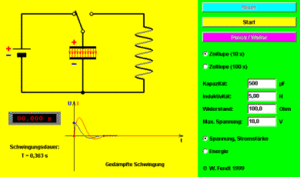
Wird ein Kondensator geladen und danach mit einer Spule leitend verbunden, fliesst ein oszillierender Strom, bis die anfänglich im Kondensator gespeicherte Energie über den immer vorhandenen Widerständen vollständig dissipiert ist. Dieser Schwingkreis ist mit der Wassersäule in einem U-Rohr vergleichbar. Was wir in der Vorlesung Trägheit als Induktivität diskutiert haben, darf auf den elektrischen Schwingkreis übertragen werden. Der ungedämpfte Schwingkreis oszilliert mit einer Schwingungsdauer von

[math]T=2\pi\sqrt{LC}[/math]

Ist der Kondensator zum Zeitnullpunkt geladen, verändert sich die Spannung cosinusartig

[math]U=U_0\cos(\omega t)[/math]

Weil der Cosinus 2-π-periodisch ist, muss das Produkt aus Schwingungsdauer T und Kreisfrequenz ω gleich 2 π sein

[math]\omega=\frac{2\pi}{T}=\frac{1}{\sqrt{LC}}[/math]

Der Reziprokwert der Schwingungsdauer heisst Frequenz f

[math]f=\frac{1}{T}=\frac{1}{2\pi\sqrt{LC}}[/math]

Die Einheit der Frequenz wird oft in Hertz (Hz) angegeben. Ein Hertz entspricht einer Schwingung pro Sekunde. Das Trägerfeld der Handystrahlung schwingt folglich je nach Modus 900 Millionen oder 1.8 Milliarden Mal in der Sekunde.

Animation von Walter Fendt

Kontrollfragen

• Wie sind Kapazität, Widerstand und Induktivität definiert? Sie müssen diese drei konstitutiven Gesetze auswendig hinschreiben können.
• Welche dieser drei Systemeigenschaften lassen sich bei Serieschaltung (hintereinander) durch einfache Addition zur Eigenschaft des Gesamtsystems zusammenfassen?
• Wie muss man bei Serieschaltung mit den andern Elementen verfahren?
• Beschreiben Sie die in einem Widerstand dissipierte Leistung einmal nur mit Hilfe der Spannung und einmal mit Hilfe der Stromstärke.
• Wie berechnet man die in einem Kondensator bei gegebener Spannung gespeicherte Energie? Wo steckt diese Energie?
• Wie gross ist die von einer Spule bei gegebener Stromstärke gespeicherte Energie? Wo steckt diese Energie?
• Wie gross ist bei einer Kapazität im Wechselstromkreis das Verhältnis von maximaler Spannung zu maximaler Stromstärke (Amplitudenverhältnis)?
• Wie gross ist dieses Verhältnis bei einer Induktivität im Wechselstromkreis?
• Schliesst man eine reine Kapazität und eine reine Induktivität an eine Wechselspannungsquelle an, läuft einmal der Strom um eine Viertelperiode voraus und einmal die Spannung. Bei welchem Element trift was zu? Wie kann man das begründen?
• Wie berechnet man die Schwingungsdauer eines LC-Kreises?

Materialien

• Skript Seite 7

Zurück zum Inhalt