Vogelschlag: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 14: | Zeile 14: | ||
Nun ersetzen wir die masselose Knautschzone durch einen hydrodynamischen Dämpfer, einen mit Wasser gefüllten Zylinder mit seitlich angebrachten Öffnungen. Ein Teil der Vogelmasse liegt damit in Form von Wasser vor, das in der Knautschzone gespeichert ist und beim Aufprall infolge des sich aufbauenden Drucks radial weg spritzt. Das zugehörige systemdynamische Modell besteht im Kern aus einer Impuls- und einer Massebilanz. Weil der Vogel weiterhin als homogener Körper modelliert wird, ist seine Geschwindigkeit gleich Impuls durch momentane Masse. Integriert man diese Geschwindigkeit über die Zeit, erhält man die Strecke, um welche die Knautschzone verkürzt wird. |
Nun ersetzen wir die masselose Knautschzone durch einen hydrodynamischen Dämpfer, einen mit Wasser gefüllten Zylinder mit seitlich angebrachten Öffnungen. Ein Teil der Vogelmasse liegt damit in Form von Wasser vor, das in der Knautschzone gespeichert ist und beim Aufprall infolge des sich aufbauenden Drucks radial weg spritzt. Das zugehörige systemdynamische Modell besteht im Kern aus einer Impuls- und einer Massebilanz. Weil der Vogel weiterhin als homogener Körper modelliert wird, ist seine Geschwindigkeit gleich Impuls durch momentane Masse. Integriert man diese Geschwindigkeit über die Zeit, erhält man die Strecke, um welche die Knautschzone verkürzt wird. |
||
Der Druck in der Knautschzone ''p<sub>e</sub>'' ist gleich der relativen Änderung des Volumens der noch vorhandenen Flüssigkeit mal das Kompressionsmodul ''K'' |
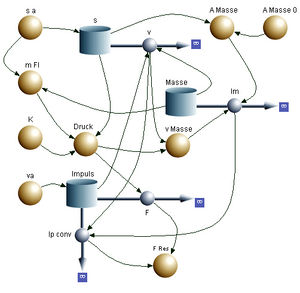
[[Bild:Vogelschlag2 SD.jpg|thumb|Systemdiagramm]]Der Druck in der Knautschzone ''p<sub>e</sub>'' ist gleich der relativen Änderung des Volumens der noch vorhandenen Flüssigkeit mal das Kompressionsmodul ''K'' |
||
:<math>p_e=K\frac{|\Delta V|}{V}</math> |
:<math>p_e=K\frac{|\Delta V|}{V}</math> |
||
| Zeile 35: | Zeile 35: | ||
:<math>F=F_{Druck}+v_{Masse}I_m=p_eA+\varrho v_{Masse}^2A</math> |
:<math>F=F_{Druck}+v_{Masse}I_m=p_eA+\varrho v_{Masse}^2A</math> |
||
Selbstverständlich geht der Impuls nicht auf konvektivem Weg auf das Flugzeug über. Bei der Umlenkung des Wassers in der vordersten Zone des Vogels geht dieser Impuls auch leitungsartig weg. Nur lässt sich das mit einem homogenen Modell nicht mehr simulieren. |
|||
==Simulationsergebnisse== |
==Simulationsergebnisse== |
||
Version vom 11. Januar 2009, 18:57 Uhr
Vogelschlag (bird strike) bezeichnet den Zusammenprall von Vögeln mit Objekten. In der Luftfahrt entsteht durch Vogelschlag jährlich ein Schaden von über einer Milliarde US-Dollar. Seit 1988 sind mehr als 200 Opfer als Folge solcher Vorfälle zu beklagen.
einfaches Modell
Der Vogel gibt beim Aufprall solange Impuls an das Flugzeug ab, bis sich die beiden Geschwindigkeit angeglichen haben. Dabei „fällt“ der Impuls in der Verformungszone von hoher zu tiefer Geschwindigkeit und setzt entsprechend Energie frei. Dieses mentale Bild liefert das einfachste Modell: der Vogel kann als starrer Körper mit masseloser Knautschzone modelliert werden. Die Knautschzone soll nun den Impulsstrom unabhängig vom Verformungszustand auf einem konstanten Wert halten. Die Stosszeit ist dann gleich der Verformung durch die mittlere Relativgeschwindigkeit oder im Maximum gleich zweimal die Länge der Knautschzone s dividiert durch die anfängliche Relativgeschwindigkeit vrel. Dividiert man den vom Vogel abzugebenden Impuls durch diese Zeit, ergibt sich die Stärke des Impulsstromes, die Kraft auf den Vogel (Abfluss) oder auf das Flugzeug (Zufluss)
- [math]F=\frac{\Delta p}{\Delta t}=\frac{mv_{rel}}{\Delta t}=\frac{mv_{rel}^2}{2s}[/math]
Multipliziert man die Kraft F mit der Verformungstrecke s, entspricht die linke Seite von Gleichung (8) der Verformungsarbeit und die rechte der kinetischen Energie des Vogels relativ zum Flugzeug.
Die Kraft nimmt mit dem Quadrat der Relativgeschwindigkeit zu. Weil ein schwerer Vogel auch über eine längere Knautschzone verfügt, dürfte die Kraft etwa mit dem Quadrat der dritten Wurzel aus dem Volumen oder der Masse zunehmen. Der Druck im Aufschlagbereich sollte dagegen nur wenig von der Masse des Vogels abhängen, weil ein doppelt so schwerer Vogel auch auf einer etwa viermal grösseren Fläche aufschlägt. Geht man von einer Taube aus (Masse 450 g), die mit einer Relativgeschwindigkeit von 150 m/s aufprallt, ergibt sich bei einer Länge der Knautschzone von 16 cm eine Kraft von 31.6 kN, was etwas mehr als dem Siebentausendfachen des Eigengewichts der Taube entspricht.
hydrodynamisches Modell
Nun ersetzen wir die masselose Knautschzone durch einen hydrodynamischen Dämpfer, einen mit Wasser gefüllten Zylinder mit seitlich angebrachten Öffnungen. Ein Teil der Vogelmasse liegt damit in Form von Wasser vor, das in der Knautschzone gespeichert ist und beim Aufprall infolge des sich aufbauenden Drucks radial weg spritzt. Das zugehörige systemdynamische Modell besteht im Kern aus einer Impuls- und einer Massebilanz. Weil der Vogel weiterhin als homogener Körper modelliert wird, ist seine Geschwindigkeit gleich Impuls durch momentane Masse. Integriert man diese Geschwindigkeit über die Zeit, erhält man die Strecke, um welche die Knautschzone verkürzt wird.
Der Druck in der Knautschzone pe ist gleich der relativen Änderung des Volumens der noch vorhandenen Flüssigkeit mal das Kompressionsmodul K
- [math]p_e=K\frac{|\Delta V|}{V}[/math]
Die den Druck erzeugende Volumenänderung entspricht der Differenz zwischen dem Volumen des nicht komprimierten Wassers (momentane Masse mFl dividiert durch die Dichte) und dem aktuellen Volumen der Knautschzone (Querschnitt A mal momentane Länge s). Der Freiraum in der Knautschzone ist also zu jedem Zeitpunkt etwas kleiner als der Quotient aus Masse und Dichte des nicht komprimierten Wassers
- [math]p_e=K\frac{V_As}{V}=K\frac{\frac{m_{Fl}}{\varrho}-As}{\frac{m_{Fl}}{\varrho}}[/math]
Weil ein Vogel als Gemisch aus etwa 85% Wasser und 15% Luft betrachtet werden kann, ist für das Kompressionsmodul nur der halbe Wert von Wasser (1 GPa) eingesetzt worden. Der Druck bestimmt dann die Geschwindigkeit des seitlich weg spritzenden Wassers
- [math]v_{Masse}=\sqrt{\frac{2p_e}{\varrho}+v^2}[/math]
Diese Formel ergibt sich aus der Energiebilanz (Gesetz von Bernoulli. Das Wasser nimmt seine momentane Bewegungsenergie mit und bekommt durch die Wirkung des Drucks noch zusätzliche Energie. Die Stärke des Massenstromes ist gleich Dichte mal Volumenstrom und der Volumenstrom gleich Geschwindigkeit mal die frei parametrisierbare Fläche AMasse der seitlichen Öffnungen im Zylinder
- [math]I_m=\varrho I_V=\varrho v_{Masse}A_{Masse}[/math]
Der Querschnitt der seitlichen Öffnungen bleibt in der ersten Stossphase konstant und geht dann zusammen mit der Länge der Knautschzone gegen Null. Damit wird verhindert, dass das Volumen der Knautschzone kleiner als Null werden kann.
Das seitlich weg spritzende Wasser nimmt anteilsmässig kinetische Energie und Impuls mit. Die Energie ist bei der Berechnung der Geschwindigkeit vMasse berücksichtigt worden. Den Impuls gibt das Wasser beim Umlenken an das Flugzeug ab, weshalb die Kraft auf das Flugzeug aus zwei Beiträgen besteht, aus Druck mal Fläche und wie bei der Rakete aus einem konvektiven Beitrag
- [math]F=F_{Druck}+v_{Masse}I_m=p_eA+\varrho v_{Masse}^2A[/math]
Selbstverständlich geht der Impuls nicht auf konvektivem Weg auf das Flugzeug über. Bei der Umlenkung des Wassers in der vordersten Zone des Vogels geht dieser Impuls auch leitungsartig weg. Nur lässt sich das mit einem homogenen Modell nicht mehr simulieren.
Simulationsergebnisse
Übernimmt man die Werte aus dem ersten Modell (Vogelmasse 450 g, Relativgeschwindigkeit 150 m/s, Länge der Knautschzone 16 cm), setzt für den Querschnitt des Vogels 22 cm2 ein und wählt für die seitlichen Öffnungen einen Gesamtquerschnitt von 10 cm2, zeigt das Modell ein plausibles Verhalten. Die Knautschzone trägt dann 78% zur Vogelmasse bei. Druckverlauf und Kraft-Weg-Verhalten ändern sich wenig, falls man die Knautschzone etwas variiert. Der Einfluss der seitlichen Öffnungen auf das Systemverhalten ist dagegen ziemlich dramatisch. Die Skizze zeigt das Kraft-Verformungs-Diagramm der Knautschzone für die Werte AMasse = 10 cm2, 12.5 cm2 und 15 cm2. Sind die seitlichen Öffnungen zu eng, baut sich zu Beginn des Aufpralls ein zu hoher Druck auf. Ein zu grosser Durchlass bremst den Vogel zu wenig stark ab, womit gegen Ende des Stossvorganges eine durch die Verengung der seitlichen Öffnungen bedingte Kraftspitze auftritt.
Messreihen mit realen Vögeln, die gegen eine feste Wand geschossen wurden, zeigen ein niederfrequentes Grundsignal, das mit dem hier simulierten gut übereinstimmt. Das Gesamtsignal (Druck-Zeit-Funktion im Zentrum des Aufschlags) enthält aber noch eine hochfrequente Oberschwingung, die von der Schockwelle herrührt [4]. Um diese Schockwelle (Impulswechselstrom) zu simulieren, müsste man den Vogel aus kleinen teilelastischen Einheiten zusammensetzen.