Lösung zu Ölfass u.a. als Speicher

1. Ölfass

Ein Gefäss mit senkrechten Wänden ist ein linearer Speicher. Deshalb ist die Kapazität gleich

[math]C_V = \frac {\Delta V} {\Delta p} = \frac {V_0} {\rho * g * h_0} = \frac {0.2 m^3} {1000 kg/m^3 * 9.81 N/kg * 1 m} = 2.04 * 10^{-5} m^3/Pa [/math]

Der Druck gegen den Umgebungsdruck steigt während der Füllzeit t_F = V₀ / I_V = 10 min linear von 0 auf 0.098 bar an.

Die Energie ist gleich

[math]W = \frac {V_0^2} {2 C_V} = 980 J [/math]

2. V-förmiges Gefäss (Rinne)

Volumenberechnung für die V-förmige Wanne

V/p-Diagramm einer V-förmigen Wanne

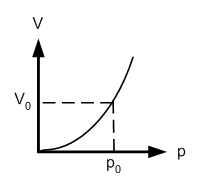
Wir erhalten das V-p-Diagramm, wenn wir Druck und Volumen in Abhängigkeit der momentanen Füllhöhe berechnen:

[math]p = \rho \cdot g \cdot h, \quad V = \frac {1} {2} \cdot b \cdot h \cdot l_0 = V_0 \cdot(\frac {h} {h_0})^2,[/math]

[math] weil \quad b / h = b_0 / h_0 \quad und \quad V_0 = \frac {1} {2} \cdot b \cdot h \cdot l_0[/math]

b ist proportional zu h, deshalb ist V proportional zu h².

Der Graph dieser Funktion ist eine nach oben geöffnete Parabelkurve durch den Nullpunkt (nichtlinearer Speicher)

[math]V = V_0 * (\frac {p} {p_0})^2[/math]

Um den Druckverlauf p(t) zu erhalten, lösen wir die Funktion V(p) nach p auf und setzen für V den Ausdruck I_V * t ein. Wir erhalten wieder eine Parabel, aber diesmal nach rechts geöffnet

[math]p = p_0 * \sqrt {\frac{I_v * t} {V_0}} = p_0 * \sqrt {\frac{t} {t_F}} [/math]

Die Energie berechnen wir im p-V-Diagramm, das ist das V-p-Diagramm von oben aber mit vertauschten Achsen: Hier erhalten wir auch eine nach rechts geöffnete Parabel: [math]p = p_0 * \sqrt {\frac{V} {V_0}}[/math]

Die Fläche unter der Kurve approximieren wir mit 2 gleich breiten "Pommes Frites". Dafür brauchen wir den Druck bei halbem Volumen: p₅₀ = 7.1 kPa. Die mittleren Drucke beider Pommes Frites betragen dann 3.5 kPa, bzw. 8.5 kPa. Nun können wir die Fläche der Pommes berechnen:

W = 3.5 kPa * 0.1 m3 + 8.5 kPa * 0.1 m3 = 1200 J.

Aufgabe