Lösung zu Aviatik 2008/Ass

Aufgabe 1

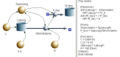
Die Spannung über Kondensator und Widerstand sinkt exponentiell mit der Zeit ab. Mit der Zeitkonstanten [math]\tau=RC[/math] = 0.6 s folgt [math]U=U_0e^{-t/\tau}[/math] = 0.944 V.

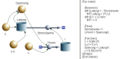
Die Bilder zeigen die Systemdiagramme sowie die Gleichungen.

• 

  RC-Glied

• 

  LC-Glied

Aufgabe 2

1. Zum Zeitpunkt 0.8 s beträgt die Beschleunigung des Wagens B 2 m/s² (1.96 m/s²) entsprechend der Steigung der Kurve im v-t-Diagramm. Folglich ist die Reibkraft gleich 80 kN (78.5 kN).
2. Der Wagen B verschiebt sich um 2.1 m (Fläche unter der Kurve im v-t-Diagramm).
3. Während sich der Puffer zusammen zieht, werden 77 kNs Impuls übertragen. Die Masse des auflaufenden Wagens beträgt damit [math]m=\frac{\Delta p}{\Delta v}[/math] = 60 t.
4. Der Wagen verschiebt sich um 0.5 m (0.509 m). Damit ist die dissipierte Energie (Reibkraft mal Verschiebung) gleich 40 kJ (39.95 kJ).

Die in Klammern gesetzten Werte sind der Simulation entnommmen.

Aufgabe 3

1. Im Bezugssystem Waschküche wirken zwei Kräfte auf das Fünffrankenstück ein, die Gewichtskraft und die Normalkraft. Beide Kräfte wirken nach unten und erteilen dem Geldstück die notwendige Beschleunigung.
2. Der Beschleunigungsvektor zeigt gegen die Mitte der Trommel. Sein Betrag ist gleich [math]a=\omega^2r[/math] = 4299 m/s² (ω = 146.6 1/s).
3. Am höchsten und am tiefsten Punkt der Bahn erzeugen Gewichts- und Normalkraft die Beschleunigung:

höchster Punkt: [math]F_G+F_N=ma[/math] daraus folgt: [math]F_N=\left(\frac ag-1\right)F_G[/math] = 437 mal die Gewichtskraft

tiefster Punkt: [math]-F_G+F_N=ma[/math] daraus folgt: [math]F_N=\left(\frac ag+1\right)F_G[/math] = 439 mal die Gewichtskraft

Aufgabe 4

1. Massenstromstärke: [math]I_m=\varrho I_V=\varrho v_1 A[/math] = 201 kg/s. Nun ist die Schubkraft gleich Geschwindigkeitsdifferenz mal die Massenstromstärke. Daraus folgt [math]v_2=\frac{F_S}{I_m}+v_1[/math] = 499 m/s.
2. Die Prozessleistung ist gleich der Differenz der Energieströme [math]P=I_{W2}-I_{W1}=\frac 12\left(v_2^2-v_1^2\right)I_m[/math] = 18.74 MW.
3. Die Schubkraft setzt sich nun aus zwei Teilen zusammen [math]F_S=0.2\left(2v_2-v_1\right)I_m+0.8\left(v_2-v_1\right)I_m[/math]. Daraus folgt [math]v_2=\frac 56\left(\frac{F_S}{I_m}+v_1\right)[/math] = 416 m/s.
4. Die Leistung setzt sich nun auch aus zwei Teilen zusammen [math]P=\frac 12\left(0.2(2v_2)^2+0.8v_2^2-v_1^2\right)I_m[/math] = 21.5 MW.

Aufgabe 5

1. Die thermisch zugeführte Energie ist gleich der Änderung der Enthalpie: [math]W=\Delta H=mc\Delta T[/math] = 150.5 MJ.
2. Zwischen dem Ausgang der Wärmepumpe und dem Wasser bleibt die Energie erhalten [math]W_{aus}=|\Delta H|[/math]. Die von der Wärmepumpe abgegebene Entropie ist demnach gleich [math]S=\frac{W_{aus}}{T_{aus}}[/math] = 414.54 kJ/K. Um diese Entropie zu fördern, benötigt die Pumpe die folgende Energie [math]W=\Delta T S[/math] = 37.3 MJ.
3. Die erzeugte Entropie ist gleich der Änderung der Entropie im Wassers minus die von der Wärmepumpe abgegebene Entropie. Für das Wassers gilt [math]\Delta S=mc\ln\left(\frac{T_2}{T_1}\right)[/math] = 474.6 kJ/K. Demnach werden bei diesem Heizverfahren 60 kJ/K Entropie erzeugt.
4. Beim verlustfreien Heizen wird die Entropie der Umgebung entnommen und direkt dem Wasser zugeführt. Die dazu notwendige Energie berechnen wir indirekt, indem wir von der Enthalpieänderung die von der Entropie aus der Umwelt abgeschleppten Energie abziehen [math]W=\Delta H-T_{Umg}S[/math] = 8 kJ.

Aufgabe 8

Aufgabe