Lösung zu Sprung aus Flugzeug: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 12. Februar 2010, 08:56 Uhr

Die Endgeschwindigkeit ist erreicht, falls der Impuls des Springers nicht mehr zunimmt, falls der gravitativ zufliessende Impuls vollständig an die Luft abgeleitet wird. Dann halten die Gewichtskraft und der Strömungswiderstand den Springer im Gleichgewicht [math] F_G - F_W = 0[/math].

Die Gleichgewichtsbedingung heisst: [math]F_G = F_W = \frac {1} {2} \rho_L v^2 c_W A[/math]. Ihre Auflösung nach der effektiven Fläche liefert [math]A_{eff} = c_W A = \frac {2 m g}{\rho_L v^2} [/math] = 0.38 m².
Das nebenstehend abgebildete Systemdiagramm (flowchart) zeigt die Modellstruktur. Wie bei allen Fragestellungen der Translationsmechanik bildet die Impulsbilanz das Rückgrat des Modells. Der Quotient aus Impuls und (träger) Masse liefert die Geschwindigkeit, die zur Falltiefe aufintegriert werden kann.
Aus dem untenstehenden Diagramm kann man entnehmen, dass der Springer schon nach zehn Sekunden über 90% seiner Endgeschwindigkeit erreicht hat. Nach etwa zwanzig Sekunden und einer Fallstrecke von gut 900 m hat der Springer die Endgeschwindigkeit von 60 m/s praktisch erreicht. In dieser Zeit würde ein Körper in Vakuum eine Geschwindigkeit von 9.81 m/s² * 20 s = 196 m/s (706 km/h) bei einer Fallstrecke von (196 m/s / 2) * 20 s = 1.96 km erreichen. Weil die Dichte der Luft nach unten zunimmt, wird ein frei fallender Mensch nach einer gewissen Zeit langsamer.
Falls sich der Fallschirm nicht öffnet, bietet eine neuseeländische Norfolk-Pinie gute Überlebenschancen, falls man schön in die nach unten dicker werdenden Äste fällt. Einen Sprung ins Wasser überlebt man bis etwa 120 km/h, falls man schwimmen kann.

Aufgabe

@@ Zeile 1: / Zeile 1: @@
 [[Bild:Sprung_Flugzeug_SD.jpg|thumb|Systemdiagramm für den Fall mit Luftwiderstand]]
-Die Endgeschwindigkeit ist erreicht, falls der [[Impuls]] des Springers nicht mehr zunimmt, falls der gravitativ zufliessende Impuls vollständig an die Luft abgeleitet wird. Dann halten die Gewichtskraft und der [[Strömungswiderstand]] den Springer im Gleichgewicht <math>F_G - F_W = 0</math>.
+Die Endgeschwindigkeit ist erreicht, falls der [[Impuls]] des Springers nicht mehr zunimmt, falls der gravitativ zufliessende Impuls vollständig an die Luft abgeleitet wird. Dann halten die Gewichtskraft und der [[Strömungswiderstand]] den Springer im Gleichgewicht <math> F_G - F_W = 0</math>.
 *Die Gleichgewichtsbedingung heisst: <math>F_G = F_W = \frac {1} {2} \rho_L v^2 c_W A</math>. Ihre Auflösung nach der effektiven Fläche liefert <math>A_{eff} = c_W A = \frac {2 m g}{\rho_L v^2} </math> = 0.38 m<sup>2</sup>.
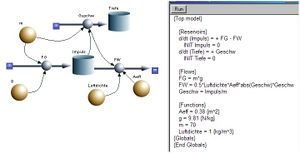
-*Das nebenstehend abgebildete [[Systemdiagramm]] (flowchart) zeigt die Modellstruktur. Wie bei allen Fragestellungen der [[Translationsmechanik]] bildet die [[Impulsbilanz]] das Rückgrat des Modells. Der Quotient aus Impuls und (träger) [[Masse]] liefert die Geschwindigkeit, die zur Falltiefe autintegriert werden kann.
+*Das nebenstehend abgebildete [[Systemdiagramm]] (flowchart) zeigt die Modellstruktur. Wie bei allen Fragestellungen der [[Translationsmechanik]] bildet die [[Impulsbilanz]] das Rückgrat des Modells. Der Quotient aus Impuls und (träger) [[Masse]] liefert die Geschwindigkeit, die zur Falltiefe aufintegriert werden kann.
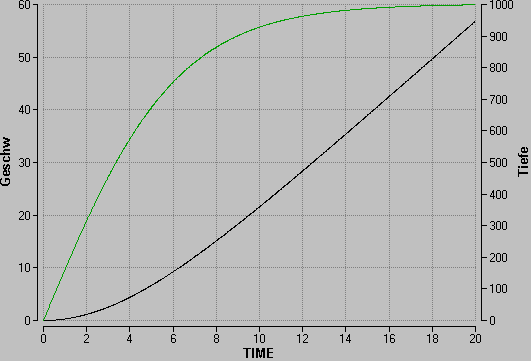
-*Aus dem untenstehenden Diagramm kann man entnehmen, dass der Springer schon nach zehn Sekunden über 90% seiner Endgeschwindigkeit erreicht hat. Nach etwa zwanzig Sekunden und einer Fallstrecke von gut 900 m hat der Springer die Endgeschwindigkeit von 60 m/s praktisch erreicht. In dieser Zeit würde ein Körper in Vakuum eine Geschwindigkeit von 196 m/s (706 km/h) bei einer Fallstrecke von 1962 m erreichen. Weil die Dichte der Luft nach unten zunimmt, wird ein frei fallender Mensch nach einer gewissen Zeit langsamer.
+*Aus dem untenstehenden Diagramm kann man entnehmen, dass der Springer schon nach zehn Sekunden über 90% seiner Endgeschwindigkeit erreicht hat. Nach etwa zwanzig Sekunden und einer Fallstrecke von gut 900 m hat der Springer die Endgeschwindigkeit von 60 m/s praktisch erreicht. In dieser Zeit würde ein Körper in Vakuum eine Geschwindigkeit von 9.81 m/s<sup>2</sup> * 20 s = 196 m/s (706 km/h) bei einer Fallstrecke von (196 m/s / 2) * 20 s = 1.96 km erreichen. Weil die Dichte der Luft nach unten zunimmt, wird ein frei fallender Mensch nach einer gewissen Zeit langsamer.
 *Falls sich der Fallschirm nicht öffnet, bietet eine neuseeländische Norfolk-Pinie gute Überlebenschancen, falls man schön in die nach unten dicker werdenden Äste fällt. Einen Sprung ins Wasser überlebt man bis etwa 120 km/h, falls man schwimmen kann.
 [[Bild:Sprung_Flugzeug_D.png]]