Gravitationsfeld

Phänomen

Impulsquellen

• Stellt man einen Körper auf eine Waage, zeigt diese einen konstanten Impulsstrom an (in der Regel ist die Waage in Kilogramm geeicht, d.h. die Stärke des an die Erde abfliessenden Impulsstromes wird auf die Masse des Körpers umgerechnet).
• Lässt man den Körper fallen, nimmt seine Geschwindigkeit und damit auch sein Impulsinhalt mit konstanter Rate zu.

Der Impuls, der über die Waage an die Erde abfliesst oder im freien Fall gespeichert wird, fliesst unsichtbar, also ohne erkennbare Zuleitung vom Gravitationsfeld in den Körper hinein (hier ist stillschweigend vorausgesetzt worden, dass die positive Richtung nach unten zeigt). Diese Zufuhr erfolgt über den ganzen Körper verteilt, also volumenmässig, und ohne Rücksicht auf die momentane Bewegung. Bildlich gesprochen quillt der Impuls vom Gravitationsfeld her in den Körper hinein. Der durch diese Quelle zugeführte Impuls wird entweder unmittelbar und kontinuierlich an die Erde abgeführt (Statik) oder mit einer gewissen Verzögerung als ganzes Paket an die Unterlage abgegeben (Fallbewegung und Aufschlag).

Schwerelosigkeit

An einem bestimmten Ort verändert sich die Geschwindigkeit aller frei fallenden Körper mit der gleichen Rate, d.h. alle Körper erfahren die gleiche Beschleunigung. Dies ist eine direkte Folge der Äquivalenz von schwerer und träger Masse: weil die schwere Masse, die mit Hilfe einer Balkenwaage durch Massenvergleich bestimmt werden kann, für alle Stoffe identisch mit der trägen Masse ist, erzeugt die gravitative Impulsquelle bei allen Körpern die gleiche Beschleunigung. Deshalb heisst die Gravitationsfeldstärke auch Fallbeschleunigung.

Die Äquivalenz von schwerer und träger Masse hat enorme Konsequenzen:

• Wirft man einen Kessel voll Steine von einer Brücke in den Fluss, bewegen sie sich mit konstanter Relativgeschwindigkeit auseinander.
• Steigt ein Astronaut aus seinem Raumschiff aus, macht er die Fallbewegung seines Raumtransporters weiterhin mit. Er fliegt ohne sich festklammern zu müssen mit.
• Alle Gegenstände im Raumschiff drin bewegen sich berührungsfrei mit sehr kleinen Reltivgeschwindigkeiten gegeneinander.
• Sobald das Zugseil bei einem Lift reisst, müssen sich die Gegenstände im Innern des Liftes nicht mehr aufeinander abstützen, um beieinander zu bleiben. Dabei spielt es keine Rolle, ob sich der Lift noch verlangsamt nach oben bewegt, den höchstn Punkt erreicht hat oder schon nach unten fällt.

Da sich im im Vakuum alle Körper bei gegebener Anfangsgeschwindigkeit ohne gegenseitige Wirkung gemeinsamen durch den leeren Raum bewegen, entsteht das Gefühl der Schwerelosigkeit. Albert Einstein hat dieses Gefühl zum Ausgangspunkt seiner Überlegungen zur Gravitation gemacht und daraus geschlossen, dass jedes frei fallende System lokal als Inertialsystem angesehen werden kann.

Gezeitenwirkung

Starre, nichtrotierende Körper, die im Vakuum frei fallen, haben zu jedem Zeitpunkt überall die gleiche Beschleunigung. Weil das Gravitationsfeld dagegen inhomogen ist, führt es nicht allen Massenelementen gleich viel Impuls pro Zeit zu. Der zufliessende Impuls muss deshalb im Innern des Körpers so umverteilt werden, dass die Beschleunigung auch wirklich konstant bleibt. Dieses Phänomen des Ausgleichs nennt man Gezeitenwirkung. Gezeitenwirkungen sind nur bei sehr grossen Körpern wie der Erde oder bei sehr starken Gravitationsfeldern zu beobachten. Am Rande von schwarzen Löchern kann die Gezeitenwirkung so stark werden, dass sogar Moleküle zerrissen werden.

Feldstärke

Der Zustand des Gravitationsfeldes kann lokal mit Hilfe der Gravitationsfeldstärke charakterisiert werden. Die Gravitationsfeldstärke beschreibt, mit welcher spezifischen Rate ein Körper Impuls mit dem Gravitationsfeld austauscht

[math]\vec g = \frac {\Sigma_{\vec p}}{m}[/math]

Die gravitative Impulsquelle Σ_p bezüglich eines Körpers heisst Gewichts-, Schwer- oder Gravitationskraft. Die Gewichtskraft ist demnach gleich dem Produkt aus der Körpereigenschaft Masse und der Raumeigenschaft Gravitationsfeldstärke

[math]\vec F_G = m \vec g[/math]

Die Gewichtskraft, die Stärke der Impulsquelle, kann nur indirekt über die Fallbewegung im Vakuum als Beschleunigung oder statisch über den zugehörigen Impulsstrom, über die Kompensationskraft, gemessen werden.

Potenzial

Quasistatische Bewegung um dr

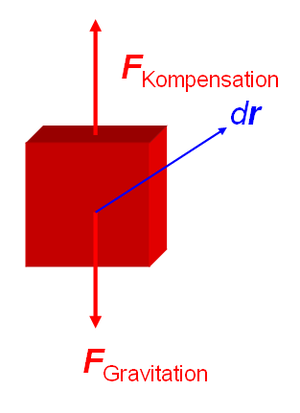
Bewegt man einen Körper auf einer geschlossenen Bahnkurve im Gravitationsfeld, ist die Arbeit der dazu notwendigen Kraft gleich Null. Dank dieser Eigenschaft kann im Gravitationsfeld eine Gravitationsenergie definiert werden. Die Gravitationsenergie ist gleich der Arbeit der Kraft, die notwendig ist, um den Körper im Gravitationsfeld quasistatisch von einem Bezugspunkt zum aktuellen Punkt zu verschieben (Überführarbeit der Kompensationskraft)

[math]W_G = \int_{\vec r_0}^{\vec r} \vec F \vec {dr} = -\int_{\vec r_0}^{\vec r} m \vec g \vec {dr} = m \int_{\vec r}^{\vec r_0}\vec g \vec {dr} = m \varphi_G[/math]

Die Gravitationsenergie ist gleich der Arbeit der Kompensatinskraft oder gleich minus die Arbeit der Gewichtskraft. Die Summe aus beiden Termen ergibt in jedem Fall Null. Da die Arbeit aller auf einen Körper einwirkenden Kräfte bei quasistatischer Bewegung im Gravitationsfeld immer gleich Null ist, speichert der Körper selber keine Energie. Nun hat man aber immer nur die Arbeit der Kompensationskraft alleine bestimmt. Deshalb wird die Graviatinsenergie statt dem Gravitationsfeld direkt dem Körper zugeschrieben und deshalb nennt man die Gravitationsenergie auch potenzielle Energie des Körpers.

Die Gravitationsenergie kann als Produkt aus der Körpereigenschaft Masse und der Raum- oder Feldeigenschaft Potenzial geschrieben und dem Körper statt dem Feld zugewiesen werden. Das Gravitatinspotenzial ist eine Eigenschaft des Feldes und berechnet sich aus dem Wegintergral über die Feldstärke

[math]\varphi_G = \int_{\vec r}^{\vec r_0}\vec g \vec {dr}[/math]

Das Gravitationspotenzial lässt sich für einfach strukturierte Felder geschlossen berechnen

• homogenes Feld: [math]\varphi_G = gh[/math]
• Himmelskörper (Bezugspunkt im Unendlichen): [math]\varphi_G = -G \frac {m}{r}[/math]
• Inneres eines homogenen Himmelskörpers (Bezugspunkt im Zentrum): [math]\varphi_G = \frac {2\pi} {3} G \rho r^2[/math]
• Zentrifugalfeld (rotierendes Bezugssystem mit Bezugspunkt auf der Achse): [math]\varphi_G = -\frac {\omega^2}{2}r^2[/math]

Jedem Vektorfeld, das wirbelfrei ist, kann ein Potenzial bezüglich eines Punktes zugewiesen werden.

Bezugssystem

Die Impulsbilanz bezüglich eines starren Körpers weist in der Regel drei Terme auf

[math]\sum_i \vec F_i + m \vec g = \dot {\vec p} = m \vec a_{MMP}[/math]

Die Oberflächenkräfte sind direkt messbar. Um die Beschleunigung des Massenmittelpunktes zu bestimmen, benötigt man ein Bezugssystem. Die Grösse des dritten Terms, die Stärke der Impulsquelle oder die Grösse der Gewichtskraft, hängt folglich von der Wahl des Bezugssystems ab, d.h. Struktur und Stärke des Gravitationsfeldes sind vom Beobachter abhängig.

Beispiele

• In einem frei fallenden System ist man schwerelos
• Befindet man sich in einem System, von dem man weiss, dass es gegen ein primäres System beschleunigt ist (z.B Flugzeug gegen Piste), muss im zweiten System ein Trägheitsfeld eingeführt werden, dessen Stärke entgegengesetzt gleich gross ist, wie die Beschleunigung des neuen Systems gegen das alte.
• Auf einem Karussell muss das auch von einem aussenstehenden Beobachter nachweisbare Feld um ein radialsymmetrisches Zentrifugalfeld und eine Kraftwirkung, die man Corioliskraft nennt, ergänzt werden.