Impuls, Impulsstrom und Kraft
Die resultierende Kraft ist gleich Masse mal Beschleunigung. Diese Gleichung, die sowohl das Grundgesetz der Mechanink umfasst als auch die dynamische Grösse Kraft mit Hilfe der kinematischen Grösse Beschleunigung definiert, soll in dieser Vorlesung auf eine umfassendere Basis gestellt werden. Dazu gehen wir vom Impuls als Primärgrösse aus. Den Impuls kennt jedes Kind unter dem Namen Wucht oder Schwung. Der Impuls ist allgegenwärtig. Ob man mit dem Hamnmer einen Nagel in die Wand schlägt oder mit dem Auto einen Inselschutzpfosten rammt, ohne Impuls würde hier gar nichts passieren.
Der Impuls und damit auch die Kraft transformieren sich wie Vektoren. Um diese Schwierigkeit zu umgehen, führen wir ein erdfestes Koordinatensystem ein und diskutieren vorderhand nur eine Komponente des Impulses. Diese eine Komponenten lässt sich durchaus mit der elektrischen Ladung oder sogar mit dem Volumen einer Flüssigkeit verglichen. Je früher Sie diese bildhafte Darstellung durchschauen, desto schneller werden Sie zu den Kernaussagen der Mechanik vorstossen.
Lernziele
Phänomene

Der angestossene Gleiter einer Luftkissenbahn bewegt sich ungebremst nach fort, bis er auf die Feder am Ende der Bahn trifft. Dieser Endanschlag wirft den Gleiter zurück, wonach dieser bis zum andern Anschlag zurück fährt, um dann wieder in die andere Richtung geworfen zu werden. Das Spiel wiederholt sich mehrmals, bis der Schwung des Gleiters aufgebraucht ist. Diesen Begriff des Schwungs gilt es nun zu schärfen. Dazu machen wir ein paar kleine Experimente
- Ein Gleiter bewegt sich mit der Geschwindigkeit 1.5 m/s auf einen ruhenden, gleich schweren Gleiter zu. Ein Klettverschluss sorgt dafür, dass die Gleiter nach dem Stoss zusammenbleiben. Die Gleiter bewegen sich nachher gemeinsam mit 0.75 m/s weiter. Weitere Experimente zeigen, dass die Geschwindigkeit unter diesen Umständen immer halbiert wird.
- Verdoppelt man die Masse des auffahrenden Gleiters, steigt die gemeinsame Geschwindigkeit auf 1 m/s an. Verdoppelt man die Masse des anfänglich ruhenden Gleiters, beträgt die Geschwindigkeit nach diesem inelastischen Stoss nur noch 0.5 m/s.
- Lässt man die beiden Gleiter mit exakt entgegengesetzt gleicher Geschwindigkeit gegeneinander gleiten, bleiben beide Körper nach einem inelastischen Stoss stehen.
- Spannt man zwischen zwei Gleiter mittels zweier Fäden eine Feder, fahren die beiden Gleiter mit entgegengesetzt gleicher Geschwindigkeit auseinander, sobald die Fäden durchgetrennt werden.
Impuls: Vorzeichen und Einheit
Im ersten Experiment führen wir mit der Hand dem Gleiter eine ganz bestimmte Menge Schwung oder eben Impuls zu. Danach behält der Gleiter seinen Impuls bei, bis er auf den Stosspartner trifft. Im Stoss überträgt der erste Gleiter die Hälfte seines Impulsinhalts auf den Partner, womit dessen Geschwindigkeit halbiert wird. Verdoppelt man die Masse des auflaufenden Gleiters, behält dieser nach dem Stoss 2/3 seines Inhaltes, womit die Geschwindigkeit nur um einen Drittel von 1.5 m/s auf 1 m/s fällt. Wird die Masse des ruhenden Körpers verdoppelt, übernimmt dieser 2/3 des Impulses und die Geschwindigkeit fällt auf 0.5 m/s. Zusammenfassend können wir festhalten; dass der Impuls
- eine bilanzierfähige Erhaltungsgrösse ist
- die Bewegung eines Körpers erzwingt (ohne Impuls keine Bewegung)
- proportional mit der Geschwindigkeit wächst
- proportional zur Masse des Speicherkörpers ist
Diese Idee hatte Christiaan Huygens schon im 17. Jahrhundert. Nur konnte man sich damals Experiment 3. und 4. nicht erklären. Wie kann durch das Zusammenfügen von zwei Mengen Nichts entstehen, d.h. was ist unter der Gleichung "Schwung plus Schwung gleich Null" zu verstehen? Und wie erklärt man das Wegfahren der beiden Gleiter unter der Wirkung der Feder. Solche Phänomene sind echt schwer zu erklären. Bei der elektrischen Ladung hat es etwa hundert Jahre gedauert, bis sich die Idee einer vorzeichenfähigen Menge durchgesetzt hat. Den Impuls hat man sogar erst im Zusammenhang mit der Quantenmechanik als bilanzierfähige Grösse akzeptiert.

Zwei Autos prallen frontal gegeneinander. Der Impuls geht während des Stosses durch die Knautschzonen von einem Auto ins andere über. Weil das eine Auto einen Impulsüberschuss und das andere einen Mangel an Impuls hatte, weisen beide Fahrzeuge nach dem Stoss keinen Impuls mehr auf. Doch welches Auto hatte vorher einen Impulsüberschuss und welches einen Mangel? Diese Frage lässt sich wie bei der elektrischen Ladung nur mit Hilfe eine Konvention beantworten. Diese Konvention ist hier rein geometrischer Natur: wir müssen bei jeder Problemstellung mit der Auszeichnung einer Richtung festlegen, wann ein Körper einen Impulsüberschuss und wann er einen Mangel aufweist.
Im SI ist die Einheit des Impulses sehr einfach gewählt worden. Der Impulsinhalt eines Körpers ist gleich dem Produkt aus Masse und Geschwindigkeit. Deshalb gilt
- [math]p_x=mv_x[/math]
Der Impulsinhalt (Formelzeichen p) wird über Masse (Formelzeichen m) und Geschwindigkeit (Formelzeichen v) gemessen. Für die Einheit des Impulses ergibt sich
- [math][p_x][/math] = kgm/s
Damit überträgt sich die Vorzeichenkonvention auf die Geschwindigkeit. Ein Körper, der eine negative Geschwindigkeit aufweist, sich also in negative Richtung bewegt, besitzt einen Impulsmangel. Dieser Sachverhalt ist analog zur Elektrizitätslehre. Wir können anhand des elektrischen Feldes, also am Potential erkennen, ob ein Körper positiv oder negativ geladen ist. Vergessen Sie aber nie, dass der Impuls wie die elektrische Ladung eine Primärgrösse der Physik ist, aber wie diese über das zugehörige Potential, die Geschwindigkeit, gemessen werden kann.
In der oben aufgeführten Formel sind sowohl der Impuls als auch die Geschwindigkeit mit x indiziert. Dieser Index weist darauf hin, dass es sich sowohl beim Impuls wie auch bei der Geschwindigkeit um Vektoren handelt. Der Impuls darf somit wie die Geschwindigkeit bezüglich der drei Richtungen eines erdfesten Koordinatensystems in drei Teile, Komponenten genannt, zerlegt werden. Jede dieser drei Komponenten ist dann wie eine eigenständige Mengen zu behandeln.
Flüssigkeitsbild
Wie in der Elektrizitätslehre führen wir zur Veranschaulichung das Flüssigkeitsbild ein. In der Translationsmechanik ist die Masse die kapazitive Grösse. Folglich erscheint die Masse im Flüssigkeitsbild als Grundgläche. Die Geschwindigkeit, die Potentialgrösse, wird zur Füllhöhe. Im Flüssigketsbild verwandeln sich alle Körper zu zylinderförmigen Gefässen, die in einem riesigen See, welche die Erde darstellt, stehen. Fährt ein Körper rückwärts, sinkt sein Pegel unter den Spiegel der Erde.
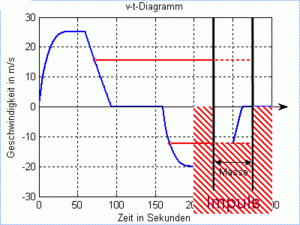
Der "Füllstand" eines Körpers wird durch die Geschwindigkeit angezeigt. Zeichnet man den zeitlichen Verlauf des Füllstandes auf, erhält man das Geschwindigkeits-Zeit-Diagramm. Dieses Diagramm hat eine dynamische Seite, gibt es doch denn Füllzustand an Impuls an, und eine kinematische (das Diagramm beschreibt ja auch noch die Bewegung des Körpers). Den Zusammenhang zwischen Bewegung, Geschwindigkeit und Flüssigkeitsbild sollten Sie sich gut einprägen. Diese drei Bilder decken einen schönen Teil der Translationsmechanik ab.
Beispiele: