Rechte-Hand-Regel
Die Rechte-Hand-Regel wird in der räumlichen Geometrie und in der Physik verwendet, um das Vektorprodukt (Kreuzprodukt) oder die Rotation genannte Ableitung eines räumlichen Vektorfeldes anzuwenden. Das dabei verwendete Koordinatensystem sollte ebenfalls die Regel der rechten Hand erfüllen.
Drei-Finger-Regel
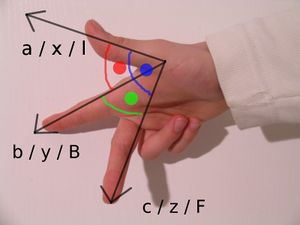
Die Orientierung des Vektors, der sich aus dem Vektorprodukt [math]\vec c=\vec a\times\vec b[/math] im dreidimensionalen Raum ergibt, wird veranschaulicht, indem der Daumen der rechten Hand in Richtung des Vektors [math]\vec a[/math] zeigt, der Zeigefinger in Richtung des Vektors [math]\vec b[/math]. Daumen und Zeigefinger liegen dabei in einer Ebene mit der Handfläche. Der Mittelfinger steht 90° ab und zeigt in Richtung des sich aus dem Vektorprodukt ergebenden Vektor [math]\vec c[/math].
Diese Regel kann auch zur Indizierung eines räumlichen Koordinatensystems verwendet werden. Die verwendeten Buchstaben sollten alphabetisch die Rechte-Hand-Regel erfüllen.
Rechte-Daumen-Regel
Die Rechte-Daumen-Regel dient dem gleichen Zweck wie die Drei-Finger-Regel. Krümmt man die Finger der rechten Hand so, dass sie beim Vektorprodukt vom Vektor [math]\vec a[/math] zum [math]\vec b[/math] zeigen, weist der Daumen in Richtung des zu bestimmenden Vektors [math]\vec c[/math].