Kegeln
Phänomen
Kegeln ist eine Sportart, bei der eine Kugel auf einer glatten Bahn gegen neun Kegel geschossen wird. Neben den drei europäischen Varianten (Asphaltbahn, Bohlenbahn und Scherenbahn) kennt man noch das amerikanische Bowling. Beim Kegeln wird die Kugel auf der Auflagebohle abgesetzt. Nach einer anfänglichen Rutschpartie geht die Kugel in ein sich verlangsamendes Rollen über.
Wir betrachten hier nur die Bewegung längs einer Geraden. Verwandte Phänome findet man beim rotierend weggeworfenen Gymnastikring (Hulahup) oder bei einem rotierend abgesetzten Kugellager (beliebtes, aber gefährliches Spiel von Lehrlingen der Maschinenbaubranche).
Theorie
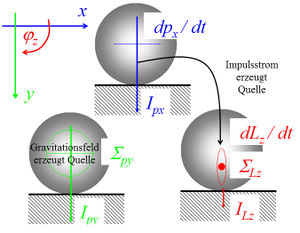
Mit der Einführung eines globalen Koordinatensystems zerlegen wir die "Bewegungsmenge" in die drei Sorten x-Impuls (Bewegungsrichtung), y-Impuls (vertikal) und z-Drehimpuls (normal zur Rotationsrichtung). Sobald die Kugel abgesetzt ist, wird der gravitativ in den Körper hineinquellende y-Impuls unmittelbar an die Unterlage abgeführt. Der zugehörige Impulsstrom belastet die Kugel auf Druck (nach unten zunehmend). Der x-Impuls fliesst anfänglich mit grosser Stärke (Rutschphase) und später nur noch im geringen Masse (Rollphase) aus der Kugel nach unten an die Unterlage weg. Dieser quer zur eigenen Bezugsrichtung fliessende x-Impulsstrom erzeugt eine z-Drehimpulsquelle. Ein Teil des über die Quelle zugeführten z-Drehimpulses fliesst reibungsbedingt ebenfalls an die Unterlage weg.
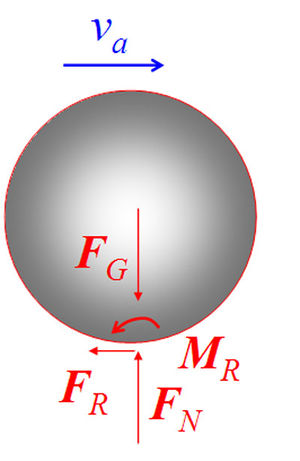
Im Schnittbild ordnet man der Stärke des volumenmässig vom Gravitationsfeld her zu- oder abfliessenden Impulses einen Pfeil zu, der nach unten zeigt, die Stärke m g hat und Gewichtskraft heisst. Die Stärke des Impulsstromes bezüglich eines Oberflächenstückes nennt man Schnitt- oder Oberflächenkraft. Die Stärke des Drehimpulsstromes heisst Drehmoment. Ein im Körper seitwärts fliessender Impulsstrom bildet eine Drehimpulsquelle (Hebelgesetz).
Im Schnittbild der Kugel zeigt das Gewicht (FG) die Stärke des Zuflusses von y-Impuls und die Normalkraft (FN) die des Abflusses an. Die Reibkraft (FR) steht für die Stärke des abliessenden x-Impulsstromes. Das Reibdrehmoment (MR) beschreibt die Stärke des abfliessenden z-Drehimpulses. Die Drehimpulsquelle wird im Schnittbild nicht eingezeichnet, muss aber bei der Formulierung der Bilanzgleichungen (Grundgesetze) über das korrekt formulierte Hebelgesetz berücksichtigt werden.
Die Stromdarstellung mag komplizierter erscheinen als der Zugang über das Schnittbild. Wenn man aber bedenkt, dass in den meisten deutschsprachigen Lehrbüchern zur Physik nicht zwichen Gewichts- und Normalkraft unterschieden wird, die Dissipation beim Rollen mit einer unsinnigen Rollreigungskraft erklärt wird und das Hebelgesetz auf die Drehachse statt auf den Massenmittelpunkt bezogen wird, sollte man ernsthaft über eine Neudarstellung der Mechanik nachdenken. Die Physik der dynamischen Systeme hat zwar noch nicht den für den Unterricht auf allen Stufen erforderliche Reifegrad erreicht, führt aber immer zu einer korrekten Darstellung der Schnittbilder.
Flüssigkeitsbild
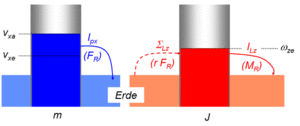
Im Flüssigkeitsbild erscheint der Impuls oder Drehimpuls als Flüssigkeit. Jeder Körper bildet ein Gefäss mit der Trägheit als Grundfläche und der zugehörigen Geschwindigkeit als Füllhöhe. Der nach unten, also quer zur Bezugsrichtung abfliessende x-Impulsstrom ist über die mittlere Länge der Stromstärke (r) mit der z-Drehimpulsquelle geometrisch verknüpft. Lässt man den reibungsbedingten Drehimpulsabfluss ausser Acht, kann die Rollgeschwindigkeit der Kugel direkt aus dem Flüssigkeitsbild berechnet werden
[math]{-}r = \frac {\Sigma_{Lz}}{I_{px}} = \frac {\Delta L_z}{\Delta p_x} = \frac {J(\omega_{ze}-0)}{m(v_{xe}-v_{xa})} = \frac {J(v_{xe}/r-0)}{m(v_{xe}-v_{xa})}[/math]
Weil die z-Drehimpulsquelle ΣLz über das Hebelgesetz mit dem Impulsstrom verknüpft ist, muss in diesem Fall auch die Drehimpulsänderung gleich minus Radius mal Impulsänderung. Durch Auflösen nach der Endgeschwindigkeit erhält man
[math]v_{xe} = \frac {m}{m + J/r^2} \cdot v_{xa}[/math]
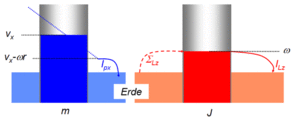
Das Flüssigkeitsbild liefert neben der anschaulichen Darstellung der Bilanz zusätzliche Informationen zur Energiebetrachtung. So ist die Prozessleistung gleich Stromstärke mal Fallhöhe oder die gespeicherte Bewegungsenergie gleich Impuls- bzw. Drehimpulsinhalt mal mittlere Pumphöhe
[math]W_{kin} = \overline{v_x} p_x = \frac {1}{2} m v_x^2[/math]
[math]W_{rot} = \overline{\omega_z} L_z = \frac {1}{2} J \omega_z^2[/math]
Der nach unten wegfliessendex-Impuls verliert je nach Drehzahl der Kugel an Potenzial. Die zugehörige Prozessleistung dient dazu, den Drehimpuls auf die entsprechende "Höhe" zu befördern
[math]P = \Delta v_z I_{pz} = \omega_z r I_{pz} = \omega_z \Sigma_{Lz} = I_W[/math]
Während der Rutschphase dissipiert der abfliessende x-Impulsstrom Energie
[math]P_{diss} = (v_x - \omega r) I_{px}[/math]
Die Energiedissipation der Rollreibung hängt dagegen nicht davon ab, ob der Körper rollt oder rutscht
[math]P_{diss} = \omega I_{Lz}[/math]