Rakete
Rakete als offenes System
Eine Rakete tauscht Impuls über das ausströmende Gas, das Gravitationsfeld und die Oberfläche aus. Wählt man die positive Richtung der z-Achse nach oben, lautet die Impulsbilanz
[math]I_{pz_{conv}} + \Sigma_{Gz} + I_{pz} = \dot p_z[/math]
Der Impulsinhalt der Rakete kann über das Kapazitivgesetz umgeschrieben werden
[math]p_z = m v_z[/math] also [math]\dot p_z = \dot m v_z + m \dot v_z[/math]
Der konvektive Impulsstrom darf als Geschwindigkeit des Gases mal Massenstromstärke geschrieben werden. Die Impulsbilanz nimmt, falls man die gravitativ bedingte Impulssenke und die Impulsstromstärke wie üblich als Kraft auf das System Rakete schreibt, die folgende Gestalt an
[math]v_{Gas}I_m + F_{G{_z}} + F_{Wid{_z}} = \dot m v_z + m \dot v_z[/math]
Ersetzt man die Geschwindigkeit des Gases durch die Geschwindigkeit der Rakete und die Ausströmgeschwindigkeit des Gases (vGas = vz - c) und nimmt noch die Massenbilanz (Im = dm/dt) dazu, vereinfacht sich die Gleichung auf
[math]c I_m + F_{G{_z}} + F_{Wid{_z}} = m \dot v_z[/math]
Bezeichnet man -c Im als Schubkraft, nimmt die Impulsbilanz die Form des Aktionsprinzips von Newton an. Diese Lesart ist natürlich unsinnig, da die Newtonmechanik nicht direkt auf offene Systeme angewendet werden kann. Der Impulsinhalt der Rakete nimmt anfänglich zu, um gegen Schluss des Brennvorgangs, dann wenn die Rakentengeschwindigkeit grösser als die Ausströmgeschwindigkeit wird, wieder abzunehmen. Die Beschleunigung der Rakete ist aber immer nach oben gerichtet.
SD-Modell
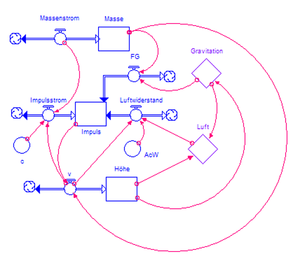
Das Systemdiagramm der Rakete zeigt im Zentrum die Impulsbilanz, darüber die Massenbilanz und darunter die Integration der Höhe aus der Geschwindigkeit. Obwohl sich hier sowohl der Impuls wie auch die Masse mit der Zeit ändern, ist die Geschwindigkeit immer noch gleich dem Quotienten aus diesen beiden Grössen. Die Systemdiagramme zur Berechnungen der Dichte der Luft und der Gravitationsfeldstärke in Funktion der Höhe sind in den beiden auf der Spitze stehenden Quadraten verpackt.
Relationen und Parameter:
| STELLA-Code | Bemerkung |
|---|---|
| Impuls(t) = Impuls(t - dt) + (Impulsstrom - Luftwiderstand - FG) * dt | Impulsbilanz |
| Masse(t) = Masse(t - dt) + (Massenstrom) * dt | Massenbilanz |
| Höhe(t) = Höhe(t - dt) + (v) * dt | Berechnung der Höhe |
| v = Impuls/Masse | dynamische Geschwindigkeit |
| Impulsstrom = Massenstrom*(v-c) | konvektiver Impulsstrom |
| Luftwiderstand = Dichte/2*v*ABS(v)*AcW | Dichte hängt von der Höhe ab |
| FG = Masse*g | Impulssenke |
| Massenstrom = IF TIME<145 THEN -2190 ELSE 0 | 145 s Brenndauer |
| g = g0*(r0/r)^2; r = Höhe+r0 | Erde als Kugel |
| Dichte = IF Höhe<Kappa/(Kappa-1)*h0 THEN Dichte0*(1-(Kappa-1)/Kappa*Höhe/h0)^(1/(Kappa-1)) ELSE 0 | isentrope Atmosphäre |
| h0 = Druck0/(Dichte0*g0) | Höhe bei inkompressibler Atmosphäre |
| INIT Masse = 482000 | Startmasse |
| AcW = 20 | effektiver Querschnitt |
| c = 2750 | Ausströmgeschwindigkeit |
| g0 = 9.8; r0 = 6.37E6 | in Gravitation |
| Dichte0 = 1.29; Druck0 = 1.013E5; Kappa = 1.4 | in Luft |
Die V2/A4-Rakete
Zur V2-Rakete, die Hitler im zweiten Weltkrieg gegen Grossbritannien eingesetzt hat, findet man im Internet folgende Daten
| Erststart: | 23. Mai 1942 |
| Vollmasse: | 12‘428 kg |
| Leermasse: | 2‘850 kg |
| Sprengkopf: | 975 kg |
| Treibstoff: | 8‘610 kg |
| Durchmesser: | 1.65 m |
| Schub: | 270 kN (300 kN Vakuum) |
| Brenndauer: | 63 s |
| spez. Impuls: | 2100 Ns/kg |
| max. Höhe: | 90 km (187 km) |
| Reichweite: | 287- 312 km |
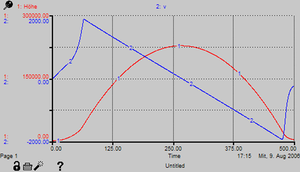
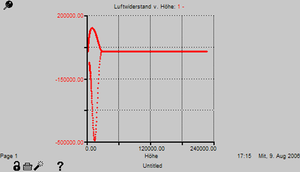
Setzt man diese Werte ins SD-Modell ein, erhält man nebenstehend abgebildeten Ergebnisse.