Satellit

Begriff

Ein Satellit (lat. Leibwächter) ist ein Körper, der einen grossen Zentralkörper auf einer elliptischen Umlaufbahn umrundet. Natürliche Satelliten, welche sich um die Sonne bewegen, werden Planeten, Planetoiden oder Kometen genannt. Sind die natürlichen Satelliten an Planeten gebunden, heissen sie Monde oder Trabanten. Künstliche Satelliten nennt man auch Orbiter.

Satelliten bewegen sich antrieblos durch den Weltraum, d.h. sie fallen um den Zentralkörper (Sonne oder Planet). Folglich wirkt auf den Satelliten nur die Gravitationskraft ein. Weil Albert Einstein die Gravitationskraft zugunsten einer rein geometrischen Erklärung abgeschafft hat, bewegen sich Satelliten gemäss der allgemeinen Relativitätstheorie kräftefrei; frei fallende Körper bewegen auf Geodäten durch die gekrümmte Raumzeit. Ein mitfliegender Mensch fühlt sich schwerelos, weil sein Bezugssystem lokal inertial ist.

Theorie

Auf frei fallende Körper wirkt nur die Gravitations-, Schwer- oder Gewichtskraft ein

[math]\vec F_G = m_s \vec g[/math]

wobei m_s für die schwere Masse und g für die Gravitationsfeldstärke steht. Die Gravitationskraft beschreibt die Stärke der Impulsquelle im Innern des Körpers. Bei frei fallenden Körpern reduziert sich die Impulsbilanz auf die Gleichsetzung der Stärke der Impulsquelle mit der Impulsänderungsrate

[math]\vec F_G = \dot {\vec p} = m_t \dot {\vec v}[/math]

wobei mit m_t die träge Masse (Impulskapazität) gemeint ist. Weil die träge Masse unter keinen Umständen von der schweren zu unterscheiden ist, dürfen beide Massen gleich gesetzt werden. Folglich kürzt sich die Masse heraus und die Impulsbilanz reduziert sich auf die Gleichsetzung der Gravitationsfeldstärke mit der Beschleunigung des Körpers

[math]\vec g = \dot {\vec v}[/math]

Die Beschleunigung des frei fallenden Körpers ist gleich der dort herrschenden Gravitationsfeldstärke (ohne Eigenfeld). Aus dieser Formulierung geht hervor, dass bei frei fallenden Körpern auf den Begriff Kraft verzichtet werden kann.

Die Gravitationsfeldstärke eines kugelförmigen Himmelskörpers nimmt mit dem Quadrat des Abstandes ab. Ist die Gravitationsfeldstärke an der Oberfläche des Himmelskörpers (g₀) sowie des Radius (r₀) gegeben, kann die Gravitationsfeldstärke an einem beliebigen Punkt ausserhalb des Himmelskörpers berechnet werden

[math]g = g_0 \frac {r_0^2}{r^2}[/math]

Eine Bemerkung muss hier leider beigefügt werden. Wer bei einem Satellitenproblem von Zentrifugalkraft redet, hat zwei wesentliche Dinge nicht begriffen

ob eine Zentrifugalkraft eingeführt werden muss oder nicht, hängt nur vom Beobachter ab. Der Begriff Zentrifugalkraft hat a priori nichts mit der Kreisbewegung eines Körpers zu tun.
Satelliten bewegen sich auf Ellipsen. Dass eine Ellipse kreisförmig ist, kommt sehr selten vor. Nur in den einführenden Lehrbüchern zur Physik bewegen sich Satelliten auf Kreisbahnen, was eine saubere Begriffsbildung bei den Lernenden eher verhindert als fördert.

Modell

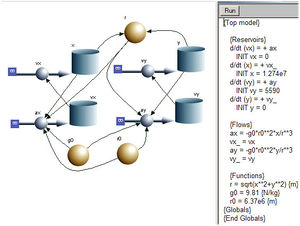
Das Systemdiagramm eines Satelliten besteht aus vier Töpfen (stock) mit je einem Rohr (flow). In diesen vier Töpfen wird die Beschleunigung bzw. die Geschwindigkeit der x- und der y-Komponente aufintegriert.

Aus den beiden Ortskomponenten (x und y) wird mit Hilfe des Satzes von Pythagoras der Abstand vom Erdzentrum (r) berechnet. Die Gravitationsfeldstärke und damit die Beschleunigung des Satelliten ist dann gleich

[math]a_x = -\frac {g_0 r_0^2 x}{r^3}[/math]

für die x-Komponenten oder

[math]a_y = -\frac {g_0 r_0^2 y}{r^3}[/math]

für die y-Komponente. Das Minuszeichen besagt, dass die Feldstärke g gegen den Ortsvektor r zeigt.

Simulation

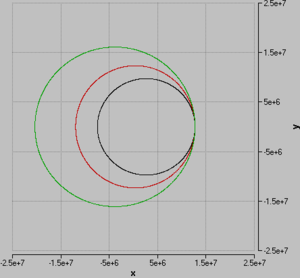
Startet man den Satelliten im Abstand des doppelten Erdradiuses auf der x-Achse und erteilt ihm eine y-Geschwindigkeit von 4800 m/s, 5500 m/s bzw. 6200 m/s ergeben sich die nebenstehend abgebildeten Bahnen.

Um die Kreisbahngeschwindigkeit zu rechnen, muss die Formel für die Beschleunigung bei einer Kreisbewegung beigezogen werden

[math]a = \frac{v^2}{r}[/math]

Setzt man diese kinematische Formel mit dem Abstandsgesetz für die Gravitationsfeldstärke gleich, erhält man die für eine Kreisbahn notwendige Geschwindigkeit in Abhängigkeit der Distanz zum Erdzentrum

[math]a = g[/math]

[math]\frac{v^2}{r} = g_0 \frac{r_0^2}{r^2}[/math]

[math]v = sqrt{\frac{g_0 r_0^2}{r}}[/math]

Die Kreisbahngeschwindigkeit beträgt bei einem Start in 6379 km über der Erdoberfläche 5.59 km/s.