Stoss
Ein Stoss ist eine kurze Wechselwirkung zwischen zwei Körpern. Bei einem Stoss wird Impuls und Drehimpuls übertragen. Die vom Impulsstrom freigesetzte Energie wird teilweise dissipiert.
Man unterscheidet zwischn
- schiefer oder versetzter Stoss: es wird Impuls und Drehimpuls übertragen
- zentraler Stoss: es wird nur Impuls übertragen
- gerader Stoss: eindimensionales Stossproblem
- inelastischer Stoss: Energie wird maximal dissipiert
- vollelastischer Stoss: es wird keine Energie dissipiert
- teilelastischer Stoss: ein Teil der beim Austausch freigesetzten Energie wird dissipiert
gerader Stoss
Der gerade Stoss verläuft längs einer Geraden. Die Dynamik dieses Stosses lässt sich mit einer einzigen Impulskomponente beschreiben und im Flüssigkeitsbild darstellen.
inelastisch
Beim inelastischen Stoss fliesst der Impuls vom Körper mit der grösseren zum Körper mit der kleineren Geschwindigkeit, bis sich die Geschwindigkeiten angeglichen haben. Im Flüssigkeitsbild erscheint der inelastische Stoss als Niveauausgleich. Die vom Impuls in der Stosszone freigesetzte Energie wird dissipiert. Die Formel für die Endgeschwindigkeit und die dissipierte Energie können direkt dem Flüssigkeitsbild entnommen werden
- [math]v_{in} = \frac {m_1 v_1 + m_2 v_2}{m_1 +m_2}[/math]
- [math]W_{diss} = \Delta v_{mittel} \Delta p = \frac {(v_1 - v_2)}{2} m_1 (v_1 - v_{in}) = \frac {(v_1 - v_2)}{2} m_2 (v_2 - v_{in})[/math]
vollelastisch
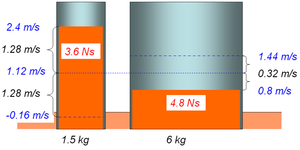
Beim vollelastischen Stoss setzt der Impuls bis zum Ausgleich der Geschwindigkeiten Energie frei. Diese Energie wird in der vollelastischen Stosszone (Feder, Gummi) zwischengespeichert. In der zweiten Stossphase, dann wenn sich die Feder oder der Gummi wieder entspannen, wird nochmals soviel Impuls wie in der ersten Phase vom anfänglich schnelleren in den andern Körper gepumpt. Im Flüssigkeitsbild erscheint der vollelastische Stoss als ein Überschwingen der beiden Flüssigkeitssäulen. Um den Endzustand zu bestimmen, spiegelt man die beiden Flüssigkeitsoberflächen am inelastischen Zustand, d.h. man klappt die Relativgeschwindigkeiten auf die andere Seite der "inelasitschen Linie".
Rein formal kann der inelastische Stoss mittels Impuls- und Energieerhaltung (vorher gleich nachher) formuliert werden
- [math]p_{tot} =p_{1v} + p_{2v} = p_{1n} + p_{2n}[/math]
- [math]W_{kin } = \frac {(p_{1v})2}{2m_1} + \frac {(p_{2v})2}{2m_2} = \frac {(p_{1n})2}{2m_1} + \frac {(p_{2n})2}{2m_2}[/math]
teilelastisch
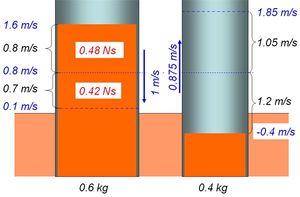
Der teilelastische oder reale Stoss liegt zwischen dem inelastischen und dem vollelastischen. Das Verhältnis zwischen der vom Impuls in der zweiten Phase aufgenommenen Energie zur vorher freigesetzten heisst Stosszahl. Weil die umgesetzte Energie proportional zum geflossenen Impuls und proportional zur Differenz der Anfangs- bzw. Endgeschwindigkeiten der beiden Körper ist, wächst der Energieumsatz quadratisch mit den Relativgeschwindigkeiten
- Stosszahl [math]\eta = \frac {W_{auf}}{W_{frei}} = \frac {(v_{nach} - v_{in})2}{(v_{vor} - v_{in})2}[/math]
Die Stosszahl ist für viele Materialien und in bestimmten Grenzen näherungsweise geschwindigkeitsunabhängig. Bei Güterwagen beträgt die Stosszahl etwa 0.33.
zentraler Stoss
Beim zentralen Stoss wird Impuls, aber kein Drehimpuls übertragen. Dieser Vorgang kann auf den geraden Stoss zurückgeführt werden, indem z.B. die x-Achse des Koordinatensystems in Stossrichtung gelegt wird. Für die x-Komponente des Impulses gelten dann die Überlegungen des geraden Stosses. Die andern beiden Impuls-Komponenten werden nicht ausgetauscht.
Mathematisch kann der zentrale Stoss durch die Impulserhaltung beschrieben werden