Lösung zu Bowling
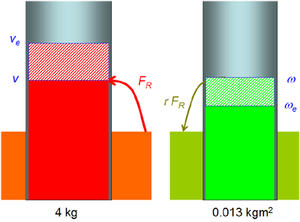
Die Umfangsgeschwindigkeit der Bowlingkugel bezüglich ihrer Mitte beträgt [math]v_U = \omega r[/math] = 6.75 m/s. Die Kugel dreht sich somit schneller, als wenn sie nur abrollen würde. Folglich wirkt die Gleitreibungskraft in Bewegungsrichtung.
- Die Gleitreibung führt der Kugel Impuls zu. Dieser Impuls fliesst in der Kugel quer zu seiner Bezugsrichtung. Längs des quer fliessenden Impulses bildet sich eine Drehimpulssenke.
- Der in der Kugel von der Berührfläche zur Mitte quer fliessender Impuls erzeugt eine Drehimpulssenke der Stärke Reibkraft mal Radius (Hebelgesetz).
- In der Rollphase muss die Umfangsgeschwindigkeit der Kugel bezüglich ihrer Mitte gleich der Geschwindigkeit dieser Mitte sein.
- Die Änderungsraten von Drehimpuls und Impuls sind über das Hebelgesetz fest verkuppelt. Folglich ist auch die Änderung des Drehimpulses fest mit der Änderung des Impulses verknüpft [math]r = \frac {F_R r}{F_R} = \frac {\left|\Delta L\right|}{\Delta p} = \frac {J(\omega - \omega_e)}{m(v_e - v)}= \frac {J(\omega - v_e/r)}{m(v_e - v)}[/math]. Löst man diese Gleichung nach der Endgeschwindigkeit auf, erhält man [math]v_e = \frac {rmv + J\omega}{rm + J/r}[/math] = 4.07 m/s. Die Kugel dreht sich dann mit einer Winkelgeschwindigkeit von 45 s-1.
- Impuls wird von der Erde in die Kugel gepumpt, Drehimpuls fliesst weg. Die dabei umgesetzte Energie ist gleich Menge mal mittlere Pump- bzw. Fallhöhe [math]W_{diss} = \Delta p \overline v - \Delta L \overline \omega[/math]. Während der Rutschphase werden 4.3 Ns Impuls im Mittel um 3.5 m/s hinauf gepumpt. Die dazu notwendige Energie stammt vom Drehimpuls (0.39 Nms), der im Mittel um 60 s-1 hinunterfällt. Die Impuls-Pumparbeit beträgt 15.2 J, der wegströmende Drehimpuls setzt 23.2 J Energie frei, folglich werden 8 J Energie zwischen Kugel und Bahn dissipiert.
Mehr zu diesem Thema unter Kegeln.