Einfaches Reservoir

Wasser ergiesst sich mit einer zeitabhängigen Stromstärke in ein Reservoir. Wie verändert sich der Inhalt des Reservoirs? Was passiert, wenn das Reservoir noch ein Leck aufweist? Dieses Problem eignet sich bestens, um in die systemdynamische Modellierungstechnik einzusteigen. Nachfolgend wird gezeigt, wie man diese Aufgabe mit BerkeleyMadonna löst.

Sobald das Programm geöffnet ist, schliessen Sie das equations-Fenster wieder und öffnen dafür ein flowchart-Fenster (im Pulldown-Menü File den Befehl New Flowchart auswählen oder mit der Tastenkombination Ctrl+Shift+N). Sollten Sie einmal ein Element zu viel gezeichnet haben, können Sie es mit der Maus aktivieren (erscheint dunkelrot) und mit Ctrl+Delete entfernen.

Aufgabe	Aktion	Reaktion
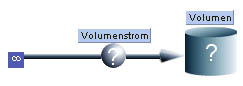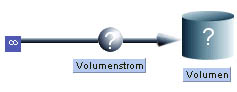
Modellieren: Ein System, bestehend aus Reservoir und Zuleitung soll modelliert werden.	Das Modell wird wie folgt erstellt: Ikon reservoir in der untersten Taskleiste durch Mausklick aktivieren Mit der Maus an die Stelle ins Systemdiagramm klicken, an welcher das Reservoir erscheinen soll Reservoir mit Volumen beschriften Ikon flow aktivieren, mit der Maus links vom Reservoir ins Systemdiagramm klicken und bis ins Reservoir hinein ziehen (Rahmen um Reservoir muss erscheinen) Flow mit Volumenstrom beschriften.
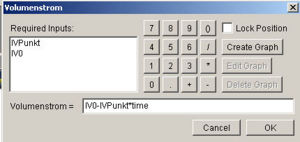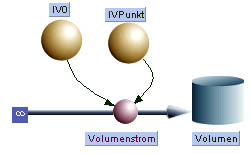
Parametrisieren: Der Eingangsstrom soll sich gemäss folgender Beziehung verändern [math]I_V=I_{V0}-I_{VPunkt}\cdot t[/math] wobei für die Stärke des Anfangsstroms (I₀) 2 l/s und für die Änderungsrate (I_VPunkt) 0.001 l/s² angenommen werden soll Der Inhalt des Reservoirs setzen wir zum Zeitnullpunkt auf Null.	Die Parameter Anfangsstrom und Änderungsrate des Stromes erhalten ein eigenes Ikon Ikon formula aktivieren, ins Systemdiagramm klicken, mit IV0 beschriften Vorgang wiederholen und mit IVPunkt anschreiben Auf die Kugel von IV0 doppelklicken, `0.002 {m3/s}` in Befehlszeile schreiben Auf die Kugel von IVPunkt doppelklicken, `1e-6 {m3/s2}` in Befehlszeile schreiben Ikon arc aktivieren, in Kugel hinein klicken und ins Ventil des Volumenstromes ziehen Auf Ventil doppelklicken und `IV0-IVPunkttime` in die Befehlszeile schreiben (die beiden Parameter lassen sich mittels Doppelklick im Fenster required inputs* aufgerufen)
Simulieren: Das Modell, bestehend aus Behälter und einem zeitabhängigen Zufluss soll nun simuliert werden. Die Simulationszeit soll 2000 Sekunden betragen und der Zeitschritt soll auf 5 Sekunden gesetzt werden. Als Integrationsmethode soll die elementare Euler-Methode ausgewählt werden.	Im Pulldown-Menü Parameters den Befehl Parameter Window (Ctrl+Shift+P)auswählen und entsprechende Zeilen neu setzten bzw. umschreiben	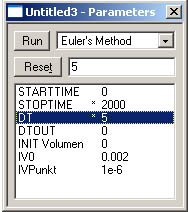Sobald die Taste 'run im Parameter Window gedrückt wird, geht ein neues Fenster auf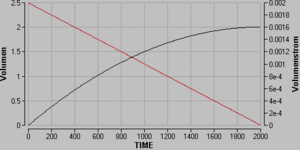