Lösung zu Aviatik 2011/3: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
==Aufgabe 2== |
==Aufgabe 2== |
||
| − | Bei der [[isentrop]]en Kompression wird [[Energie]] in Form von [[Arbeit] zugeführt. Die [[Entropie]] des Gases bleibt konstant. Beim [[isochor]]en Auskühlen |
+ | Bei der [[isentrop]]en Kompression wird [[Energie]] in Form von [[Arbeit]] zugeführt. Die [[Entropie]] des Gases bleibt konstant. Beim [[isochor]]en Auskühlen geht die Energie zusammen mit der Entropie als [[Wärme]] weg. Die [[Stoffmenge]] kann mit Hilfe der Anfangsbedingungen berechnet werden |
::<math>n=\frac{p_1V_1}{RT_1}</math> = 0.0727 mol. |
::<math>n=\frac{p_1V_1}{RT_1}</math> = 0.0727 mol. |
||
1. Das Druck-Volumen-Verhalten folgt aus der Beschreibung der isentropen Zustandsänderung <math>\left(pV^\kappa = konst\right)</math>: |
1. Das Druck-Volumen-Verhalten folgt aus der Beschreibung der isentropen Zustandsänderung <math>\left(pV^\kappa = konst\right)</math>: |
||
::<math>p_2=p_1\left(\frac{V_1}{V_2}\right)^{\kappa}</math> = 22.6 bar, daraus folgt <math>T_2=T_1\frac{p_2V_2}{p_1V_1}</math> = 748 K |
::<math>p_2=p_1\left(\frac{V_1}{V_2}\right)^{\kappa}</math> = 22.6 bar, daraus folgt <math>T_2=T_1\frac{p_2V_2}{p_1V_1}</math> = 748 K |
||
| + | 2. Die Kompressionsarbeit ist gleich der Erhöhung der inneren Energie. Diese hängt von der Temperaturänderung ab |
||
| + | ::<math>W_{12}=\Delta W=n\hat c_V\Delta T</math> = 680 J |
||
| + | 3. Bei der isochoren Abkühlung hängt die Entropieänderung nur von der Temperaturänderung ab |
||
| + | ::<math>\Delta S_{23}=n\hat c_V\ln\left(\frac{T_3}{T_2}\right)</math> = -1.39 J/K |
||
| + | 4.Bei der Wärmeleitung bleibt die Energie erhalten und die Entropie nimmt maximal zu. Die Entropieaufnahme der Umgebung ist gleich zugeführte Wärmeenergie geteilt durch Temperatur der Umgebung |
||
| + | ::<math>S_{Umg}=\frac{W_{th}}{T_{Umg}}=\frac{|\Delta W_{23}|}{T_{Umg}}=\frac{\Delta W_{12}}{T_{Umg}}</math> = 2.28 J/K |
||
| + | :Die produzierte Entropie ist gleich der von der Umgebung aufgenommenen Entropie minus der vom Gas abgegebenen Entropie |
||
| + | ::<math>S_{prod}=S_{Umg}-|\Delta S_{23}|</math> = 0.89 J/K |
||
| + | |||
| + | ==Aufgabe 3== |
||
| + | ::<videoflash>KV6n8o6sa4c|649|360</videoflash> |
||
| + | |||
| + | ==Aufgabe 4== |
||
| + | Zur Lösung dieser Aufgabe sollte unbedingt ein [[Flüssigkeitsbild]] skizziert werden. |
||
| + | |||
| + | 1. Das [[Drehmoment]] kann auf zwei Arten berechnet werden: |
||
| + | :1. Drehmoment (Drehimpulsstromstärke) mal Zeit ist gleich Drehimpulsinhalt: <math>M\Delta t = L = (J_1+J_2)\omega_{End}</math> also <math>M=\frac{(J_1+J_2)\omega_{End}}{\Delta t}</math> = 1000 Nm |
||
| + | :2. Der zweite Weg führt über die [[Drehimpulsbilanz]] (Grundgesetz der Rotationsmechanik). Weil das zweite Schwungrad zuerst noch nicht mitgedreht wird, gilt kurz nach dem Zeitpunkt 1 s: <math>M=J\dot\omega_1</math>, wobei die Winkelbeschleunigung als Steigung aus dem Diagramm heraus gelesen werden kann. |
||
| + | 2. Die [[Prozessleistung]] ist gleich Stromstärke des Drehimpulses mal Differenz der beiden Winkelgeschwindigkeiten (Fallhöhe). Die Drehimpulsstromstärke oder das Drehmoment kann auf zwei Arten berechnet werden: |
||
| + | :1. Zwischen etwa 3 s und 5 s steigt ''ω''<sub>2</sub>-Funktion linear mit der Zeit. Daraus lässt sich die Winkelbeschleunigung (Steigung im ''ω''-Zeit-Diagramm) und der Drehimpulsstrom (Drehmoment) berechnen: |
||
| + | ::<math>M_{12}=J_2\dot\omega_2</math> = 660 Nm. Die [[Prozessleistung]] ist dann gleich <math> P(M)=M_{12}(\omega_1-\omega_2)</math> = 8.6 kW |
||
| + | :2. Da beide Winkelgeschwindigkeits-Zeit-Funktionen gleich stark ansteigen, sind beide Winkelbeschleunigungen gleich gross (stationärer Zustand). Der zufliessende Drehimpuls verteilt sich entsprechend der Massensträgheitsmomente auf beide Schwungräder: |
||
| + | ::<math>M_{12}=M\frac{J_2}{J_1+J_2}</math> = 666 Nm. Die [[Prozessleistung]] berechnet sich dann wie beim ersten Lösungsweg. |
||
| + | 3. Die Arbeit ist gleich der über die Zeit aufintergrierten Leistung. Daraus kann, weil das Drehmoment konstant ist, die Formel "Arbeit gleich Drehmoment mal Winkel" abgeleitet werden (der Winkel entspricht der Fläche unter dem ''ω''-Zeit-Diagramm): |
||
| + | ::<math>W(M)=\int Pdt=M\int\omega dt=M\Delta\varphi</math> = 94 kJ |
||
| + | 4. Di dissipierte Energie ist gleich der zusammen mit dem Drehimpuls zugeführten minus die Rotationsenergie: |
||
| + | ::<math>W_{diss}=W(M)-W_{rot}=M\Delta\varphi-\frac{J_1+J_2}{2}\omega_{End}</math> = 28 kJ |
||
| + | |||
| + | ::<videoflash>gLodGIfvEKk|649|360</videoflash> |
||
| + | |||
| + | ==Aufgabe 5== |
||
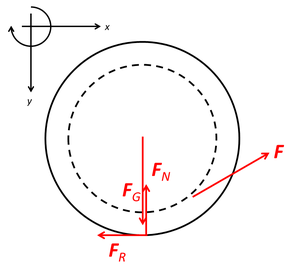
| + | [[Datei:Aviatik 11 3 L5.png|thumb|Schnittbild der Fadenspule]] |
||
| + | Hier ist das Standardverfahren der Mechanik gefragt: [[Freischneiden]], Grundgesetze ([[Impulsbilanz]] und [[Drehimpulsbilanz]]) formulieren, kinematische Verknüpfungen sowie weitere Gesetze zufügen und Gleichunssystem lösen. |
||
| + | 1. Vier Kräfte wirken auf die Fadenspule ein: Gewichtskraft, Fadenkraft, Normal- und Reibungskraft (Trockenreibung mit den Zuständen Haft- und Gleitreibung). |
||
| + | |||
| + | 2. In der Ebene müssen drei Bilanzgleichungen (zwei Impulsbilanzen und eine Drehimpulsbilanz) formuliert werden. Dazu kommen wahlweise eine kinematische Verknüpfung sowie das Gleitreibungsgesetz: |
||
| + | ::<math>F\cos 30^\circ-F_R=ma</math> |
||
| + | ::<math>F_G-F_N-F\sin 30^\circ=0</math> |
||
| + | ::<math>-Fr+F_RR=J\alpha</math> |
||
| + | ::<math>a=\alpha R</math>, falls die Fadenspule rollt |
||
| + | ::<math>F_R=\mu F_N</math>, falls die Fadenspule rutscht |
||
| + | |||
| + | 3. Aus der ''y''-Impulsbilanz folgt, dass die Normalkraft 24 N beträgt. Das Gleitreibungsgesetz liefert dann für die Gleitreibung 9.62 N. Löst man die ''x''-Impulsbilanz nach der Beschleunigung auf, erhält man 6.74 m/s<sup>2</sup>. Aus der Drehimpulsbilanz erhält man für die Winkelbeschleunigung einen Wert von -35.6 1/s<sup>2</sup>. |
||
| + | |||
| + | 4. Im Grenzfall zwischen Rutschen und Rollen gelten alle fünf Gleichungen gleichzeitig. Die Auflösung des Systems nach der Fadenkraft liefert: |
||
| + | ::<math>F=\mu mg\left(\frac{1+\frac{mR^2}{J}}{\cos 30^\circ+\frac{mrR}{J}+\mu\sin 30^\circ\left(1+\frac{mR^2}{J}\right)}\right)</math> = 21.1 N |
||
| + | |||
| + | '''[[Aviatik 2011/3|Aufgabe]]''' |
||
Aktuelle Version vom 29. Juni 2012, 21:53 Uhr
Aufgabe 1
1. Das Triebwerk schneidet duch die Bewegung des Flugzeuges einen Zylinder aus der Lauft aus. Der zugehörige Massenstrom ist gleich
- [math]I_m=\varrho I_V = \varrho v A[/math]. Daraus folgt für die Eintrittsöffnung
- [math]A=\frac{I_m}{\varrho v}[/math] = 9.28 m2 oder d = 3.44 m
2. Die Geschwindigkeitszunahme berechnet sich aus dem Impulsaustausch
- [math]F=\Delta v I_m[/math] oder [math]\Delta v=\frac{F}{I_m}[/math] = 121 m/s. Daraus folgt für die Austrittsgeschwindigkeit [math]v_{aus}=v_{ein}+\Delta v[/math] = 371 m/s.
- Die Stromstärke der kinetischen Energie ist gleich Dichte der kinetischen Energie mal Stärke des Volumenstromes. Daraus folgt für die Prozessleistung
- [math]P_1=\frac{v_{aus}^2-v_{ein}^2}{2}I_m[/math] = 21.7 MW
3. Die Kraft auf das Triebwerk ist gleich der Impulsaustauschraten der beiden Luftströme
- [math]F=\left(0.1\Delta v_1+0.9\Delta v_2\right)I_m[/math] daraus folgt
- [math]\Delta v_2=\frac{F-0.1\Delta v_1I_m}{0.9I_m}[/math] = 116 m/s
- v2a = 366 m/s
4. Für die Prozessleistung gilt
- [math]P_1=\frac{v_{1aus}^2-v_{1ein}^2}{2}0.1I_m[/math] = 3.06 MW
- [math]P_1=\frac{v_{2aus}^2-v_{2ein}^2}{2}0.9I_m[/math] = 18.7 MW
- [math]P_{total}= P_1+P_2[/math] = 21.8 MW
Aufgabe 2
Bei der isentropen Kompression wird Energie in Form von Arbeit zugeführt. Die Entropie des Gases bleibt konstant. Beim isochoren Auskühlen geht die Energie zusammen mit der Entropie als Wärme weg. Die Stoffmenge kann mit Hilfe der Anfangsbedingungen berechnet werden
- [math]n=\frac{p_1V_1}{RT_1}[/math] = 0.0727 mol.
1. Das Druck-Volumen-Verhalten folgt aus der Beschreibung der isentropen Zustandsänderung [math]\left(pV^\kappa = konst\right)[/math]:
- [math]p_2=p_1\left(\frac{V_1}{V_2}\right)^{\kappa}[/math] = 22.6 bar, daraus folgt [math]T_2=T_1\frac{p_2V_2}{p_1V_1}[/math] = 748 K
2. Die Kompressionsarbeit ist gleich der Erhöhung der inneren Energie. Diese hängt von der Temperaturänderung ab
- [math]W_{12}=\Delta W=n\hat c_V\Delta T[/math] = 680 J
3. Bei der isochoren Abkühlung hängt die Entropieänderung nur von der Temperaturänderung ab
- [math]\Delta S_{23}=n\hat c_V\ln\left(\frac{T_3}{T_2}\right)[/math] = -1.39 J/K
4.Bei der Wärmeleitung bleibt die Energie erhalten und die Entropie nimmt maximal zu. Die Entropieaufnahme der Umgebung ist gleich zugeführte Wärmeenergie geteilt durch Temperatur der Umgebung
- [math]S_{Umg}=\frac{W_{th}}{T_{Umg}}=\frac{|\Delta W_{23}|}{T_{Umg}}=\frac{\Delta W_{12}}{T_{Umg}}[/math] = 2.28 J/K
- Die produzierte Entropie ist gleich der von der Umgebung aufgenommenen Entropie minus der vom Gas abgegebenen Entropie
- [math]S_{prod}=S_{Umg}-|\Delta S_{23}|[/math] = 0.89 J/K
Aufgabe 3
Aufgabe 4
Zur Lösung dieser Aufgabe sollte unbedingt ein Flüssigkeitsbild skizziert werden.
1. Das Drehmoment kann auf zwei Arten berechnet werden:
- 1. Drehmoment (Drehimpulsstromstärke) mal Zeit ist gleich Drehimpulsinhalt: [math]M\Delta t = L = (J_1+J_2)\omega_{End}[/math] also [math]M=\frac{(J_1+J_2)\omega_{End}}{\Delta t}[/math] = 1000 Nm
- 2. Der zweite Weg führt über die Drehimpulsbilanz (Grundgesetz der Rotationsmechanik). Weil das zweite Schwungrad zuerst noch nicht mitgedreht wird, gilt kurz nach dem Zeitpunkt 1 s: [math]M=J\dot\omega_1[/math], wobei die Winkelbeschleunigung als Steigung aus dem Diagramm heraus gelesen werden kann.
2. Die Prozessleistung ist gleich Stromstärke des Drehimpulses mal Differenz der beiden Winkelgeschwindigkeiten (Fallhöhe). Die Drehimpulsstromstärke oder das Drehmoment kann auf zwei Arten berechnet werden:
- 1. Zwischen etwa 3 s und 5 s steigt ω2-Funktion linear mit der Zeit. Daraus lässt sich die Winkelbeschleunigung (Steigung im ω-Zeit-Diagramm) und der Drehimpulsstrom (Drehmoment) berechnen:
- [math]M_{12}=J_2\dot\omega_2[/math] = 660 Nm. Die Prozessleistung ist dann gleich [math] P(M)=M_{12}(\omega_1-\omega_2)[/math] = 8.6 kW
- 2. Da beide Winkelgeschwindigkeits-Zeit-Funktionen gleich stark ansteigen, sind beide Winkelbeschleunigungen gleich gross (stationärer Zustand). Der zufliessende Drehimpuls verteilt sich entsprechend der Massensträgheitsmomente auf beide Schwungräder:
- [math]M_{12}=M\frac{J_2}{J_1+J_2}[/math] = 666 Nm. Die Prozessleistung berechnet sich dann wie beim ersten Lösungsweg.
3. Die Arbeit ist gleich der über die Zeit aufintergrierten Leistung. Daraus kann, weil das Drehmoment konstant ist, die Formel "Arbeit gleich Drehmoment mal Winkel" abgeleitet werden (der Winkel entspricht der Fläche unter dem ω-Zeit-Diagramm):
- [math]W(M)=\int Pdt=M\int\omega dt=M\Delta\varphi[/math] = 94 kJ
4. Di dissipierte Energie ist gleich der zusammen mit dem Drehimpuls zugeführten minus die Rotationsenergie:
- [math]W_{diss}=W(M)-W_{rot}=M\Delta\varphi-\frac{J_1+J_2}{2}\omega_{End}[/math] = 28 kJ
Aufgabe 5
Hier ist das Standardverfahren der Mechanik gefragt: Freischneiden, Grundgesetze (Impulsbilanz und Drehimpulsbilanz) formulieren, kinematische Verknüpfungen sowie weitere Gesetze zufügen und Gleichunssystem lösen. 1. Vier Kräfte wirken auf die Fadenspule ein: Gewichtskraft, Fadenkraft, Normal- und Reibungskraft (Trockenreibung mit den Zuständen Haft- und Gleitreibung).
2. In der Ebene müssen drei Bilanzgleichungen (zwei Impulsbilanzen und eine Drehimpulsbilanz) formuliert werden. Dazu kommen wahlweise eine kinematische Verknüpfung sowie das Gleitreibungsgesetz:
- [math]F\cos 30^\circ-F_R=ma[/math]
- [math]F_G-F_N-F\sin 30^\circ=0[/math]
- [math]-Fr+F_RR=J\alpha[/math]
- [math]a=\alpha R[/math], falls die Fadenspule rollt
- [math]F_R=\mu F_N[/math], falls die Fadenspule rutscht
3. Aus der y-Impulsbilanz folgt, dass die Normalkraft 24 N beträgt. Das Gleitreibungsgesetz liefert dann für die Gleitreibung 9.62 N. Löst man die x-Impulsbilanz nach der Beschleunigung auf, erhält man 6.74 m/s2. Aus der Drehimpulsbilanz erhält man für die Winkelbeschleunigung einen Wert von -35.6 1/s2.
4. Im Grenzfall zwischen Rutschen und Rollen gelten alle fünf Gleichungen gleichzeitig. Die Auflösung des Systems nach der Fadenkraft liefert:
- [math]F=\mu mg\left(\frac{1+\frac{mR^2}{J}}{\cos 30^\circ+\frac{mrR}{J}+\mu\sin 30^\circ\left(1+\frac{mR^2}{J}\right)}\right)[/math] = 21.1 N