Aviatik 2006/2

==Studiengang Aviatik der ZHW=- Erlaubte Hilfsmittel: Taschenrechner, selbstverfasste Formelsammlung

1.

Aufgabe 1

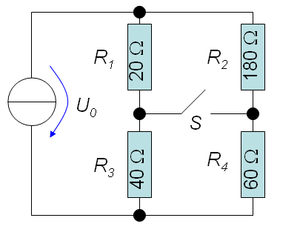
Vier Widerstände (R₁ = 20 Ω, R₂ = 180 Ω, R₃ = 40 Ω, R₄ = 60 Ω) werden wie skizziert mit einer Spannungsquelle (12 V) zu einer Schaltung verbunden. Zu Beginn sei der Schalter S offen.

1. Wie stark sind die in den beiden Zweigen (R₁ und R₃ sowie R₂ und R₄) fliessenden Ströme?
2. Welche Leistung wir im kleinsten Widerstand (R₁ = 20 Ω) umgesetzt?
3. Welche Spannung misst man über dem offenen Schalter?
4. Nun wird der Schalter geschlossen. Wie gross ist nun die Spannung über dem Widerstand R₃ (40 Ω)?

2. Nebenstehend das Geschwindigkeits-Zeit-Diagramm eines nach oben geworfenen Fussballes (Masse 330 g).

1. Wie hoch steigt der Ball auf?
2. Wie gross ist die Beschleunigung des Balles zum Zeitpunkt 0.5 s?
3. Mit welcher Kraft wirkt dann (zum Zeitpunkt 0.5 s) die Luft auf den Ball ein?

   

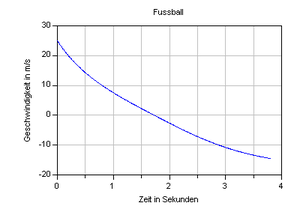
   Geschwindigkeits-Zeit-Diagramm

3.

Spannungs-Zeit-Diagramm

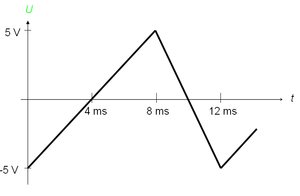
Ein Kondensator (Kapazität 40 μ F oder 0.04 mF) und eine ideale Spule (Induktivität 250 μ H oder 0.25 mH) sind parallel (nebeneinander) mit einer Spannungsquelle verbunden. Die Spannung verändert sich gemäss der nebenstehend skizzierten Graphik zwischen den Werten -5 V und 5 V. Anfänglich fliesst kein Strom durch die Spule.

1. Wie viel Energie speichert der Kondensator maximal?
2. Wie stark ist der im Kondensatorkreis fliessende Strom zum Zeitpunkt 6 ms?
3. Wie stark ist der im Spulenkreis fliessende Strom zu diesem Zeitpunkt?
4. Wie stark wird der durch die Spule fliessende Strom maximal?

4. Auf ein Luftkissenfahrzeug ist vertikal ein kleines Holzbrett quer zur Bewegungsrichtung montiert (Masse von Brettchen und Luftkissenfahrzeug 800 g). Nun trifft in Fahrtrichtung eine Pistolenkugel (Masse 15 g) mit einer Geschwindigkeit von 260 m/s normal auf das ruhende Holzbrett auf.

zu Aufgabe 4

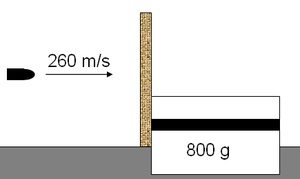
1. Wie schnell würde sich das Luftkissenfahrzeug bewegen, wenn die Kugel im Holzbrett stecken bleibt?
2. Weil die Kugel das Brettchen durchschlagen hat, gleitet das Luftkissenfahrzeug nur mit 1 m/s weg. Wie schnell fliegt die Kugel nach dem Durchschlag weiter?
3. Wie viel Energie ist im Holz dissipiert worden?

5.

zu Aufgabe 5

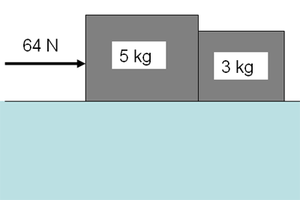
Auf zwei ruhende Klötze (Massen des linken Klotzes 5 kg, Masse des rechten Klotzes 3 kg) wirkt von links her während zwei Sekunden eine konstante Kraft von 64 N ein. Infolge dieser Einwirkung erfahren die Klötze eine Beschleunigung von 2 m/s².

1. Wie gross ist die auf beide Körper einwirkende Gleitreibungskraft?
2. Die Gleitreibung sei proportional zu den Massen der Klötze. Wie gross ist die Kraft, mit welcher der schwerere Klotz auf den leichteren einwirkt?
3. Wie viel Energie wird in der gesamten Reibschicht (beide Klötze) in diesen zwei Sekunden dissipiert?

6. Ein Auto (Masse 1500 kg) prallt auf Glatteis mit einer Geschwindigkeit von 60 km/h frontal gegen ein zweites (Masse 1200 kg), das ruht. Beide Autos besitzen dieselbe Knautschzone. Die Knautschzone beginnt sich bei 100 kN zu verformen. Danach steigt die zur Verformung einer Knautschzone notwendige Kraft um 2 kN pro Zentimeter an.

1. Skizzieren Sie ein Systemdynamik-Modell (flowchart) für diesen Prozess!
2. Geben Sie die Berechnungsformel für die Geschwindigkeit und die Stosskraft (Impulsstromstärke) an.
3. Skizzieren Sie die gegebene Charakteristik der Knautschzone (Kraft-Verformungs-Diagramm). Wie könnte die Charakteristik für eine reale Knautschzone aussehen?

Lösung