Lösung zu Fahrzeug mit drei Klötzen

Zwei reibungsfrei gelagerte Körper bewegen sich nach der Zufuhr einer gegebenen Energiemenge voneinander weg. Dieses Problem soll nun zuerst rein algebraisch gelöst werden. Danach ist die Lösung der hier gestellten Aufgabe keine Hexerei mehr.

Impuls trennen im Flüssigkeitsbild

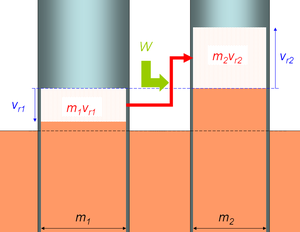
Anfänglich bewegen sich beide Körper mit der gleichen Geschwindigkeit in eine Richtung. Mit der zugeführten Energie wird nun Impuls aus dem ersten Körper in den zweiten gepumpt, womit die Geschwindigkeit des ersten um v_r1 kleiner und die des zweiten um v_r2 grösser wird. Der Index r steht für relativ zur ursprünglichen Geschwindigkeit. Der Impuls bleibt erhalten und die zugeführte Energie ist gleich geförderter Impuls mal mittlere "Hubhöhe"

[math]m_1v_{r1}=m_2 v_{r2}[/math]

[math]W=\Delta p\overline{\Delta v}=m_1v_{r1}\frac{v_{r1}+v_{r2}}{2}=\frac{m_1}{2}v_{r1}^2\left(1+\frac{m_1}{m_2}\right)[/math]

Die Relativgeschwindigkeit ist hier für beide Körper als positiv angenommen worden. Diese Annahme stützt sich auf das Flüssigkeitsbild. Orientiert man sich an diesem Bild, macht man kaum je einen Vorzeichenfehler. In der zweiten Umformung ist die Relativgeschwindigkeit des zweiten Körpers mit Hilfe der Impulserhaltung (erste Gleichung) in die des ersten umgerechnet worden. Löst man nach der Geschwindigkeit des ersten Körpers auf, folgt die allgemeine Formel

[math]v_{r1} = \sqrt{\frac{2W}{m_1(1+ \frac {m_1}{m_2})}}[/math]

Weisen die Körper gleiche Masse auf, übernehmen sie je die Hälfte der Energie. Ansonsten nimmt der leichtere Körper mehr Energie auf. Im Extremfall, wenn es sich beim zweiten Körper um die Erde handelt, übernimmt der wegfliegende Körper die ganze Energie. Dann nennt man die von diesem Körper zusammen mit dem Impuls transportierte Energie kinetisch.

miteinander

Werden die drei Klötze miteinander weggeschleudert, verteilt sich die Energie gleichmässig auf Klötze und Luftkissenfahrzeug. Die oben hergeleitete Formel liefert für diesen Prozess die folgende Relativgeschwindigkeit

[math]v_r = \sqrt{\frac {W}{m}}= \sqrt{\frac {12 J}{1.5 kg}} = [/math] 2.83 m/s

Das Luftkissenfahrzeug bewegt sich danach um diesen Betrag schneller, gleitet also mit 3 m/s + 2.83 m/s = 5.83 m/s nach rechts.

nacheinander

Die zweite Problemstellung ist analog, aber in drei Schritten zu lösen. Zudem ist zwischen der Relativgeschwindigkeit des Fahrzeuges und derjenigen des Klotzes zu unterscheiden. Bei jedem Wurf nimmt die Geschwindigkeit des Fahrzeuges gemäss der oben abgeleiteten Formel um den folgenden Beitrag zu

[math]v_{rF} = \sqrt{\frac{2W}{m_F(1+ \frac {m_F}{m_K})}}[/math]

Setzt man für die Masse des Fahrzeuges nacheinander 2.5 kg, 2 kg und 1.5 kg ein (4 J für W und 0.5 kg für m_K), erhält man für das Luftkissenfahrzeug die folgenden Zunahmen der Geschwindigkeit: 0.730 m/s, 0.894 m/s und 1.155 m/s. Die Endgeschwindigkeit erhöht sich damit um 0.73 m/s + 0.89 m/s + 1.16 m/s = 2.78 m/s auf 3 m/s + 2. 78 m/s = 5.78 m/s.

Drei Klötze gleichzeitig fort werfen bringt bei gleicher Energie eine höhrere Geschwindigkeit als ein gestaffelter Abwurf, weil der zweite und dritte Klotz zuerst mit dem Wagen und danach gegen ihn beschleunigt werden muss. Doch genau dieses Handicap besitzt der Raketenantrieb, geht doch ein grosser Teil des Brennstoffes mit der Rakete weg, bevor er nach hinten weggeblasen wird. Gegen Brennschluss bewegt sich das Gas oft langsamer aus der Düse, als sich die Rakete nach oben bewegt.

Aufgabe