Lösung zu Kreisprozess Stirling

• 

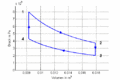
  T-S-Diagramm

• 

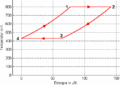
  p-V-Diagramm

1. Die Isothermen verlaufen im T-S-Diagramm horizontal, im p-V-Diagramm bilden sie Hyperbeln. Die Isochoren ergeben im T-S-Diagramm eine Schar von Exponentialfunktionen, im p-V-Diagramm verlaufen sie vertikal. Im Stirling-Zyklus wird in den isothermen Prozessen Entropie von einem heissen Bad aufgenommen bzw. an ein kälteres abgegeben. Dazwischen muss die Temperatur gesenkt bzw. angehoben werden. Die beim Abkühlen frei zusetzende Entropie muss für das nachfolgende Heizen reversibel zwischengelagert werden.
2. Das universelle Gasgesetz (thermische Zustandsgleichung) liefert bei bekanntem Druck und gegebener Temperatur das Volumen: [math]V_1=\frac{nRT_1}{p_1}[/math] = 10 mol * 8.31 J/K/mol * 800 K / 80 bar = 0.00831 m³ und [math]V_3 = \frac{nRT_3}{p_3}[/math] = 10 mol * 8.31 J/K/mol * 430 K / 20 bar = 0.0179 m³ (40 g Helium sind 10 mol, n = m / m_mol = 40 g / 4 g = 10 mol).
3. Die bei der isothermen Expansion aufgenommene Entropie beträgt [math] S_{12} = \Delta S_{12} = n R \ln{\frac{V_2}{V_1}}[/math] = 10 mol * 8.31 J/K/mol * ln(0.0179 m³ / 0.00831 m³) = 63.8 J/K. Die Entopieänderung des anderen isothermen Schrittes ist entgegengesetzt gleich: [math]S_{34} = \Delta S_{34} = n R \ln{\frac{V_4}{V_3}}[/math] = 10 mol * 8.31 J/K/mol * ln(0.00831 m³ / 0.0179 m³) = - 63.8 J/K (Logarithmus des reziproken Volumenverhältnis).
4. Die beim isochoren Aufheizen aufzunehmende Entropie S₄₁ ist gleich der Entropieänderung [math]\Delta S_{41} = - \Delta S_{23} = n \frac{3}{2} R \ln{\frac{T_{1}}{T_{4}}}[/math] = 10 mol * 1.5 * 8.31 J/K/mol * ln(800 K / 430 K) = 77.4 J/K.
5. In reversibel geführten Kreisprozessen entspricht die Nettoarbeit der durch den Kreisprozess ausgeschnittenen Fläche im p-V-Diagramm. Diese Energie wird von der Entropie beim Durchlaufen des Stirling-Zyklus freigesetzt. Im T-S-Diagramm entspricht sie ebenfalls der vom Prozess eingeschlossenen Fläche. In den beiden isochoren Schritten ist die Arbeit 0 und die Fläche unter der T-S-Kurve für diese beiden Schritte entspricht deshalb der Änderung der inneren Energie. Weil die Änderung der inneren Energie nur von den beiden entgegengesetzt gleichen Temperaturänderungen abhängig ist, sind die Flächen unter der T-S-Kurve für die beiden isochoren Schritte ebenfalls entgegengesetzt gleich und kompensieren sich. Für die im T-S-Diagramm eingeschlossene Fläche müssen wir deshalb nur die Flächen unter den horizontalen Schritten berücksichtigen. Diese entsprechen der Energie, welche die Entropie ΔS₁₂ bei der Temperatur T₁ aufnimmt und bei T₃ wieder abgibt (ΔS₃₄ = - ΔS₁₂): [math]W_{frei}=\Delta S_{12}(T_{12}-T_{34})[/math] = 63.8 J/K * (800 K - 430 K) = 23.6 kJ.

Aufgabe