Lösung zu Prozessleistung Gravitation

1. Eine Fallhöhe von 110 m ergibt eine Differenz des Gravitationspotenzials (Gravitationsspannung) von 9.81 m/s² * 110 m = 1.08 kJ/kg. Ein Massenstrom von 10 Millionen Kilogramm pro Sekunde, der über diese Potenzialdifferenz fällt, setzt eine Leistung von 1.08 kJ/kg * 10⁷ kg/s = 10.8 GW frei.
2. P = (2365 m - 481 m) * 9.81 N/kg * 75'000 kg/s = 1.39 GW
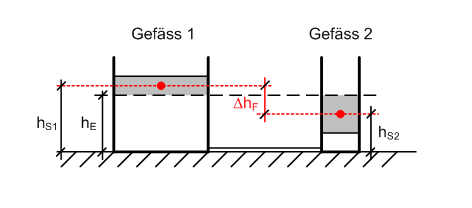3. Der Wasserspiegel wird am Ende in beiden Gefässen 34.2 cm ( = h_E in der Skizze) über den Gefässböden liegen (h_E = totales Volumen von 0.04 m² * 0.4 m + 0.008 m² * 0.05 m = 0.0164 m³ dividiert durch gesamten Querschnitt von 0.04 m² + 0.008 m² = 0.048 m²). Im Ausgleichsprozess fliessen insgesamt 1000 kg/m³ * (0.4 m - 0.342 m) * 0.04 m² = 2.32 kg Wasser (schattierte Fläche mit Schwerpunkt) im Mittel um 17.5 cm (Fallhöhe Δh_F = h_S1 - h_S2, Höhe der Schwerpunkte h_S1 = 37.1 cm und h_S2) = 19.6 cm) hinunter. Dabei werden 0.175 m * 9.81 N/kg * 2.32 kg = 3.98 J Energie dissipiert.
4. Die Fallhöhe muss mindestens 18.8 m betragen: Δh = Δφ_G / g = (P_grav / I_m) / g = 4.6 MW / 25'000 kg/s / 9.81 N/kg .

Die Gravitationsfeldstärke ist in allen Berechnungen gleich 9.81 N/kg gesetzt worden.

Aufgabe