Lösung zu Zylinder mit Seil

Seilkraft nach unten

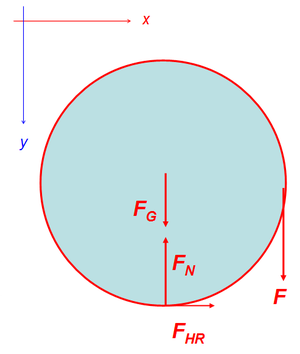
1. Auf den Zylinder wirken neben dem Gravitationsfeld und dem Seil nur noch die beiden Träger ein. Diese Einwirkung kann in eine Normalkraft und eine Haftreibungskraft zerlegt werden.

2. Die Bilanzgesetze lauten

x-Impuls: [math] F_{HR} = \dot p_x = m \dot v_x[/math]

y-Impuls: [math] F_G + F - F_N = \dot p_y = 0[/math]

z-Drehimpuls: [math] F r - F_{HR} r = \dot L_z = J_z \dot \omega_z[/math]

3. und 4. Die Impulsbilanz in y-Richtung hat keinen Einfluss auf die gestellten Fragen. Als weitere Beziehung benötigt man aber noch die Rollbedingung. Somit ergeben sich drei Gleichungen

x-Impuls: [math] F_{HR} = m \dot v[/math]

z-Drehimpuls: [math] F r - F_{HR} r = J \dot \omega[/math]

Rollbedingung: [math] v = r \omega[/math] oder [math]\dot v = r \dot \omega[/math]

Das sind drei Gleichungen mit den 3 Unbekannten [math]\dot v, \dot \omega[/math] und [math]F_{HR}[/math]. Daraus können die Antworten zu den beiden letzten Fragen berechnet werden

[math] \dot v = \frac {F}{m + J/r^2}[/math] = 40 N / (6 kg + 0.0075 kgm² / (0.05 m)²) = 4.44 m/s²

[math] F_{HR} = m \dot v = F \frac {m}{m + J/r^2}[/math] = 6 kg * 4.44 m/s² = 26.7 N

Aufgabe