Stirling-Zyklus
Der Striling-Zyklus ist wie der Carnot-Zyklus oder der Ericsson-Zyklus ein reversibler Kreisprozess des idealen Gases, der zwischen zwei Wärmebädern der Temperatur T12 und Temperatur T34 abläuft. Im Gegensatz zum Carnot- oder zum Ericsson-Zyklus verlaufen die beiden Prozesse, bei denen die Temperatur abgesenkt oder angehoben werden, isochor. Der Stirling-Zyklus ist der Grenzprozess des Stirlingmotors
Teilprozesse
- isotherme Expansion von 1 nach 2: Das Gas nimmt Entropie aus dem heissen Bad auf und gibt die damit aufgenommene Energie (Wärme) in Form von Arbeit an den verschiebbaren Kolben weiter. Die innere Energie des Gases bleibt bei diesem Prozess konstant.
- isochores Abkühlen von 2 nach 3: Das Gas gibt Entropie an den Regenerator weg. Die von der Entropie an den Regenerator weg geführte Energie (Wärme) entstammt dem Gas, entspricht also der Änderung der inneren Energie des Gases.
- isotherme Kompression von 3 nach 4: Das Gas gibt Entropie ans kalte Bad ab. Die dabei abgeführte Energie (Wärme) muss vom Kolben zugeführt werden, da die innere Energie des Gases wie beim ersten Teilprozess konstant bleibt.
- isochores Heizen von 4 nach 1: Das Gas nimmt Entropie vom Regenerator auf. Die damit zugeführte Energie (Wärme) bleibt im Gas drin und entspricht der Änderung der inneren Energie des Gases.
| Zustandsdiagramme | |
|---|---|
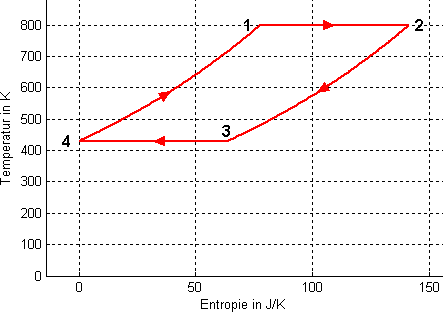
|
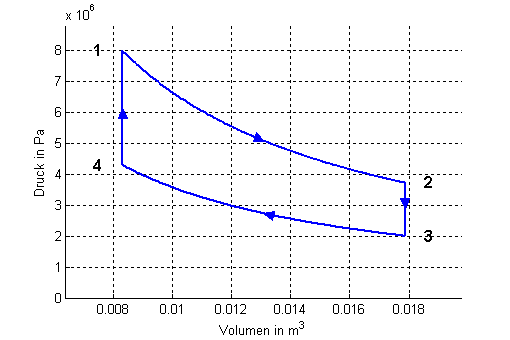
|
Wie beim Ericsson-Zyklus verändert sich die Entropie des Gases beim Absenken und Anheben der Temperatur. Würde das Gas diese Entropie beim Kühlen unkontrolliert ans kalte Bad abgeben und beim Heizen vom warmen Bad beziehen, würde die thermisch hinunter fallende Entropie weitere Entropie erzeugt. Dies würde den Wirkungsgrad des Zyklus vermindern. Dank der Zwischenspeicherung im Regenerator wird im Idealfall keine Entropie erzeugt und der Zyklus erreicht den Carnot-Wirkungsgrad von
- [math]\eta_C=1-\frac{T_{34}}{T_{12}}[/math]
Ohne Regenerator wäre der Wirkungsgrad bestenfalls gleich
- [math]\eta=\frac{W_{nutz}}{W_{zu}}=\frac{T_{12}-T_{34}}{T_{12}+\frac{c_V}{\Delta s}(T_{12}-T_{34})}[/math]
wobei cV für die spezifische Wärmekapazität bei konstantem Volumen steht und mit Δs die Änderung der spezifischen Entropie bei der isothermen Expansion gemeint ist (nutzbare Entropie pro Kilogramm Gas). Der Wirkungsgrad wird grösser, falls pro Zyklus vom Gas mehr Entropie bei konstanter Temperatur aufgenommen wird.
Links
- Animation
- Stirling-Kreisprozess auf Youtube