Umwälzpumpe
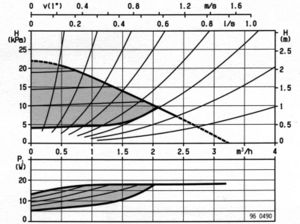
Auf dem nebenstehend abgebildeten Datenblatt finden Sie Charakteristik einer Umwälzpumpe. Dank eingebauter Regelung kann die Pumpe im grau markierten Bereich arbeiten. Ohne Regelung liegen alle Arbeitspunkte auf der oberen Begrenzungslinie. Die von links unten nach rechts oben verlaufenden Linien charakterisieren das Verhalten verschiedener hydraulischer Kreise.
Machen Sie sich zuerst ein paar Gedanken zum oberen Diagramm:
- Die Volumenstromstärke ist in drei verschiedenen Skalen angegeben. Sind die Einheiten sinnvoll gewählt? Für wen hat man diese Skalen gezeichnet? Stimmt die Umrechnung?
- Wie kann man in diesem Diagramm die von der Pumpe abgegebene Leistung erkennen?
- Durch welche Funktion werden die von links unten nach rechts oben verlaufenden Linien beschrieben?
- Jeder Punkt in diesem Diagramm steht für eine bestimmte Volumenstromstärke und eine bestimmte Druckdifferenz (Druckaufbau bei der Pumpe, Druckabbau im Kreis).
- Wie bewegt sich der Punkt in diesem Diagramm, wenn man die Pumpenleistung drosselt?
- Wie bewegt sich der Punkt, wenn man bei ungedrosselter Leistung der Pumpe den Widerstand im Kreis verändert?
Bei einem bestimmten Kreis vermag die Pumpe maximal 1.5 m3/h zu fördern.
- Bestimmen Sie für diesen Kreis die maximale und die minimale Leistung der Pumpe aus dem Datenblatt.
- Welche Leistung müsste eine grössere Pumpe abgeben, damit 6 m3/h durch diesen Kreis flössen?
- Wie gross wäre die Volumenstromstärke, wenn man zwei solche Kreise in Serie geschaltet mit der bei 1. gegebenen Pumpe bei ungedrosselter Leistung betreiben würde?
- Wie gross wäre die Volumenstromstärke, wenn man zwei solche Kreise parallel geschaltet mit der bei 1. gegebenen Pumpe bei ungedrosselter Leistung betreiben würde?
Hinweis: Prozessleistung; ist die Strömung in den Kreisen laminar oder turbulent? wie beschreibt man das charakteristische Verhalten der verschiedenen Kreise (Druck-Volumenstromstärke-Funktion)?
Quelle: FH 2003