Ladungs- und Energiespeicher: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (27 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
==Kapazität einer Kugel== |
==Kapazität einer Kugel== |
||
In den [[Ladung und Strom|einführenden Experimenten]] haben wir isolierte Metallkugeln mit einem an Wolle geriebenen Glasstab geladen oder mit einem Bernsteinstab entladen. Die mit den Kugeln verbundenen [[Elektrometer]] zeigten dann das zugehörige Potenzial, die Spannung gegen Erde, an. Nun nimmt eine grosse Kugel bei gleichem Potenzial mehr Ladung auf als eine kleine |
In den [[Ladung und Strom|einführenden Experimenten]] haben wir isolierte Metallkugeln mit einem an Wolle geriebenen Glasstab geladen oder mit einem Bernsteinstab entladen. Die mit den Kugeln verbundenen [[Elektrometer]] zeigten dann das zugehörige Potenzial, die Spannung gegen Erde, an. Nun nimmt eine grosse Kugel bei gleichem Potenzial mehr Ladung auf als eine kleine, d.h. grosse Kugel verfügt über mehr [[kapazitives Gesetz|Kapazität]] als die kleine. In der [[Elektrodynamik]] wird die Kapazität analog zur [[Hydrodynamik]] definiert: die Kapazität ist gleich dem Verhältnis von gespeicherter Ladung zu der dadurch verursachten Spannung |
||
:<math>C=\frac{Q}{U}</math> |
:<math>C=\frac{Q}{U}</math> |
||
Die Kapazität misst man in Coulomb pro Volt oder Farad (F, benannt nach ''Michael Faraday'') |
Die Kapazität misst man in Coulomb pro Volt oder '''Farad''' (F, benannt nach ''Michael Faraday'') |
||
:1 F = 1 C/V = 1 As/V |
:1 F = 1 C/V = 1 As/V |
||
[[Bild:Ladung Fluessigkeitsbild.png|thumb|geladene Körper im Flüssigkeitsbild]] Die Ladung einer Metallkugel (es könnte auch ein anders geformter Körper sein) erzeugt im Aussenraum ein elektrisches Feld, das durch Ladungen |
[[Bild:Ladung Fluessigkeitsbild.png|thumb|geladene Körper im Flüssigkeitsbild]] Die Ladung auf einer Metallkugel (es könnte auch ein anders geformter Körper sein) erzeugt im Aussenraum ein elektrisches Feld, das durch die Ladungen der umgebenden Körper, speziell der Erdoberfläche, begrenzt wird. Die Spannung ist deshalb gegen die Erde zu messen (Potenzial). Verändert man die Lage der umgebenden Körper, beeinflusst dies das elektrische Feld und damit auch das Potenzial der Kugel. Befindet sich die Metallkugel (Radius ''r'') weit weg von allen leitfähigen Körperoberflächen, lässt sich die zugehörige Kapazität mit einer einfachen Formel beschreiben |
||
:<math>C=4\pi\varepsilon_0 r</math> |
:<math>C=4\pi\varepsilon_0 r</math> |
||
Epsilon steht für die elektrische Feldkonstante (''ε<sub>0</sub>'' = 8.854 10<sup>-12</sup> F/m). Interessanterweise nimmt die Kapazität einer Kugel nicht proportional zum Volumen oder zur Oberfläche sondern linear mit dem Radius zu. Um dies zu zeigen, |
Epsilon steht für die elektrische Feldkonstante (''ε<sub>0</sub>'' = 8.854 10<sup>-12</sup> F/m). Interessanterweise nimmt die Kapazität einer Kugel nicht proportional zum Volumen oder zur Oberfläche sondern linear mit dem Radius zu. Um dies zu zeigen, müsste man mehr über die Gesetze, welche das [[elektromagnetisches Feld|elektromagnetische Feld]] beschreiben, wissen. |
||
Die Zusammenhänge zwischen Ladung, Kapazität und Potenzial lassen sich sehr schön im [[Flüssigkeitsbild]] darstellen. Stellt man sich die Ladung als Flüssigkeit, die Körper als zylindrische Gefässe und die Kapazität als Querschnitt dieser Gefässe vor, verwandelt sich das Potenzial in eine Füllhöhe. Die Ladung |
Die Zusammenhänge zwischen Ladung, Kapazität und Potenzial lassen sich sehr schön im [[Flüssigkeitsbild]] darstellen. Stellt man sich die Ladung als Flüssigkeit, die Körper als zylindrische Gefässe und die Kapazität als Querschnitt dieser Gefässe vor, verwandelt sich das Potenzial in eine Füllhöhe. Die Ladung, die als Kapazität mal Potenzial geschrieben werden kann, erscheint dann im Flüssigkeitsbild als Grundfläche mal Höhe. |
||
==Kondensatoren== |
==Kondensatoren== |
||
Umhüllt man eine elektrisch geladene Metallkugel mit einer zweiten, die geerdet ist, |
Umhüllt man eine elektrisch geladene Metallkugel mit einer zweiten, die geerdet ist, fliesst von der zweiten Kugel gleich viel Ladung weg, wie auf der ersten gespeichert ist. Dieses Phänomen, [[Influenz]] genannt, führt dazu, dass ausserhalb der beiden Kugeln kein elektrisches Feld mehr nachzuweisen ist. Mit der zweiten Kugelschale, Abschirmung genannt, erreicht man zwei Dinge: erstens stört das eingeschlossene Feld keine andern Systeme im Aussenraum und zweitens wird das elektrische Feld räumlich begrenzt, was die Kapazität beträchtlich erhöht. |
||
Die Kapazität eines Kugelkondensators (zwei konzentrische Kugeln mit je einem Anschluss) ist gleich |
|||
:<math>C=4\pi\varepsilon_0\frac{r_2r_1}{r_2-r_1}</math> |
:<math>C=4\pi\varepsilon_0\frac{r_2r_1}{r_2-r_1}</math> |
||
wobei mit ''r<sub>1</sub>'' der Aussenradius der Innenkugel und mit ''r<sub>2</sub>'' der Innenradius der Aussenkugel gemeint ist. |
wobei mit ''r<sub>1</sub>'' der Aussenradius der Innenkugel und mit ''r<sub>2</sub>'' der Innenradius der Aussenkugel gemeint ist. |
||
Die elektrische Ladung sitzt auf der Innenkugel aussen und auf der Aussenkugel innen. Der Grund dafür ist in der Leitfähigkeit der Kugelschalen zu suchen. Würde das elektrische Feld in das Metall eindringen, würde es dort gemäss dem Ohmschen Gesetz einen Strom antreiben. Folglich darf sich das elektrische Feld nur zwischen den Metallteilen ausdehnen und die Ladungen, die dieses Feld aufbauen, müssen auf der Metalloberfläche sitzen. |
|||
[[Bild:Kondensator.png|thumb|Kondensator mit Dielektrikum]] Je kleiner der Spalt zwischen den beiden Kugeln (''r<sub>2</sub> - r<sub>1</sub>''), desto kürzer das Feld, desto kleiner die Spannung bei gegebener Ladung und um so grösser die Kapazität. Wählt man den Spalt immer enger, darf die Spannung zwischen den beiden Kugeln nicht zu gross werden |
[[Bild:Kondensator.png|thumb|Kondensator mit Dielektrikum]] Je kleiner der Spalt zwischen den beiden Kugeln (''r<sub>2</sub> - r<sub>1</sub>''), desto kürzer das Feld, desto kleiner die Spannung bei gegebener Ladung und um so grösser die Kapazität. Wählt man den Spalt immer enger, darf die Spannung zwischen den beiden Kugeln nicht zu gross werden. Sonst würden die Elektronen durch das starke Feld aus dem negativ geladenen Teil heraus gerissen und gegen den positiven geschleudert. Um solche Kurzschlussströme zu verhindern, füllt man den Raum zwischen den beiden Teilen des Kondensators mit einem isolierenden Material, dem [[Dielektrikum]], auf. Das Dielektrikum ermöglicht nicht nur eine höhere Spannung, sondern schwächt auch noch das durch die Ladung erzeugte Feld ab. Diese Schwächung des Feldes durch das Dielektrikum wird mit der Dielektrizitätszahl beschrieben. Nun nennt man das Produkt aus '''elektrischer Feldkonstante''' (''ε<sub>0</sub>'') und '''Dielektrizitätszahl''' (''ε<sub>r</sub>'') '''Dielektrizitätskonstante''' (''ε'') |
||
:<math>\varepsilon=\varepsilon_r\varepsilon_0</math> |
:<math>\varepsilon=\varepsilon_r\varepsilon_0</math> |
||
Diese Konstruktion mag etwas kompliziert tönen, hat aber den Vorteil, dass die [[ |
Diese Konstruktion mit elektrischer Feldkonstante, Dielektrizitätszahl und Dielektrizitätskonstante mag etwas kompliziert tönen, hat aber den Vorteil, dass die [[kapazitives Gesetz|Kapazitäten]] der [[Kondensator]]en einfach zu berechnen sind. Man nimmt die im Vakuum berechnete Kapazität und schreibt statt ''ε<sub>0</sub>'' einfach nur ''ε''. So lautet die Formel für den Kugelkondensator mit Dielektrikum |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
:<math>C=\varepsilon\frac{A}{d}</math> |
|||
wobei ''A'' für die Fläche der einen Platte und ''d'' für den Abstand zwischen den Platten steht. |
wobei ''A'' für die Fläche der einen Platte und ''d'' für den Abstand zwischen den Platten steht. |
||
==hydroelektrische Analogie== |
==hydroelektrische Analogie== |
||
[[Bild:Hydraulischer Kondensator.png|thumb|hydraulischer Kondensator]] Der [[Kondensator]] speichert netto keine elektrische Ladung, weil sich die Ladung auf seinen beiden Teilen zu Null kompensiert. Das elektrische Feld, das beim Laden des Kondensators aufgebaut wird, erstreckt sich denn auch nur zwischen den beiden |
[[Bild:Hydraulischer Kondensator.png|thumb|hydraulischer Kondensator]] Der [[Kondensator]] speichert netto keine elektrische Ladung, weil sich die Ladung auf seinen beiden Teilen zu Null kompensiert. Das elektrische Feld, das beim Laden des Kondensators aufgebaut wird, erstreckt sich denn auch nur zwischen den beiden Metallflächen (bei neueren Kondensatoren nur über eine Oxidschicht oder eine Schicht aus wenigen Molekülen). Fliesst nun in einem der beiden Anschlüsse ein elektrischer Strom zu, geht im andern Anschluss genau der gleich starke Strom weg. Von aussen könnte man meinen, dass der elektrische Strom einfach nur so durchfliesst. Doch mit der geflossenen Ladung ''Q'' steigt auch die Spannung ''U'' über den beiden Anschlüssen (mit ''Q'' meint man immer die geflossene oder auf einem Teil des Kondensators gespeicherte Ladung). |
||
Das hydraulische Analogon ist nebenstehend skizziert. Pumpt man die Flüssigkeit mit dem Volumen ''Δ |
Das hydraulische Analogon ist nebenstehend skizziert. Pumpt man die Flüssigkeit mit dem Volumen ''ΔV'' auf der einen Seite hinein, steigt der Druckunterschied zwischen den beiden Anschlüssen um ''Δp''. Das Verhältnis zwischen ''ΔV'' und ''Δp'' ist die [[Widerstand und Speicher|hydraulische Kapazität]]. Die hydraulische Kapazität ist konstant, solange sich die Federn linear verhalten. Das Gesamtvolumen dieses hydraulischen Speichers bleibt wie die elektrische Ladung des Kondensators konstant: was auf der einen Seite hinein kommt, geht auf der andern augenblicklich wieder weg. |
||
==Energiespeicher== |
==Energiespeicher== |
||
Der Begriff Kapazität, welcher das Verhältnis zwischen geflossener Ladung und Änderung der Spannung beschreibt, kann auch direkt auf den Strom |
Der Begriff Kapazität, welcher das Verhältnis zwischen geflossener Ladung und Änderung der Spannung beschreibt, kann auch direkt auf den Strom umdefiniert werden. Dazu formulieren wir die Bilanz bezüglich der einen Hälfte des Kondensators (Strom ist gleich Änderungsrate der Ladung) und ersetzen die Ladung durch Kapazität mal Spannung. Die Änderungsrate der Ladung wird so durch Kapazität mal Änderungsrate der Spannung ersetzt |
||
| ⚫ | |||
| ⚫ | [[Bild:Kondensator entladen FB.png|thumb|Ladungsausgleich im Flüssigkeitsbild]] Fliesst nun in einem Draht des Kondensators ein konstanter Strom zu, steigt die Spannung linear in der Zeit. Damit nimmt die Leistung ebenfalls kontinuierlich zu. Die vom Stromkreis auf das elektrische Feld des Kondensators übertragene Energie ist deshalb gleich mittlere Spannung mal geflossene Ladung oder halbe Endspannung mal geflossene Ladung |
||
| ⚫ | |||
| ⚫ | [[Bild:Kondensator entladen FB.png|thumb|Ladungsausgleich im Flüssigkeitsbild]] |
||
:<math>W=\frac{U}{2}Q=\frac{C}{2}U^2=\frac{Q^2}{2C}</math> |
:<math>W=\frac{U}{2}Q=\frac{C}{2}U^2=\frac{Q^2}{2C}</math> |
||
Wieder hilft uns das [[Flüssigkeitsbild]] den Sachverhalt besser zu verstehen. Denken wir uns den einen Teil des Kondensators geerdet, dann erscheint der andere |
Wieder hilft uns das [[Flüssigkeitsbild]] den Sachverhalt besser zu verstehen. Denken wir uns den einen Teil des Kondensators geerdet, dann erscheint der andere Teil im Flüssigkeitsbild als Topf. Um Flüssigkeit aus einem grossen See in ein Reservoir zu pumpen, muss die am Schluss im Reservoir vorhandene Flüssigkeit (Ladung ''Q'') um die halbe Höhe (mittlere Spannung) angehoben werden. |
||
'''Beispiel:''' |
|||
| ⚫ | |||
| ⚫ | Ein Kondensator mit der Kapazität ''C<sub>1</sub>'', der bis auf die Spannung ''U<sub>1</sub>'' aufgeladen worden ist, wird mit einem zweiten Kondensator (Kapazität ''C<sub>2</sub>'', Spannung ''U<sub>2</sub>'') verbunden. Wie sieht der Endzustand aus und wie viel Energie wird [[Dissipation|dissipert]]? Diese Aufgabe ist mit Hilfe des [[Flüssigkeitsbild]]es spielend leicht zu beantworten. Wieder denken wir uns die eine Seite der Kondensatoren geerdet. Dann können die beiden andern Teile als Töpfe und die angelegte Spannung als Füllhöhe dargestellt werden. Der Ausgleichsvorgang ist im nebenstehenden Bild dargestellt. Die Spannung, die schlussendlich an beiden Kondensatoren anliegt, ist direkt dem Bild zu entnehmen. Die [[Dissipation|dissipierte]] Energie ist dann gleich geflossene Ladung mal mittlere Fallhöhe. |
||
==RC-Glied== |
==RC-Glied== |
||
| Zeile 73: | Zeile 80: | ||
*Potenzial treibt den Strom entsprechend des Widerstandes |
*Potenzial treibt den Strom entsprechend des Widerstandes |
||
*Leistung und Energie als zweite Ebene (Buchhaltung) hinzufügen |
*Leistung und Energie als zweite Ebene (Buchhaltung) hinzufügen |
||
Die Gleichungen für dieses System findet man im Fenster ''"Equations"'' von BerkeleyMadonna. Lässt man für die Beschreibung die Energiebetrachtung weg, kann der Rest in eine einzige Gleichung umgeformt werden |
|||
:<math>U+RC\dot U=0</math> |
:<math>U+RC\dot U=0</math> |
||
| Zeile 81: | Zeile 88: | ||
:<math>U=U_ae^{-t/\tau}</math> |
:<math>U=U_ae^{-t/\tau}</math> |
||
''τ'' |
''τ'' ist die Zeitkonstante. Nun ist der Wert der Zeitkonstanten gleich dem Produkt aus Widerstand und Kapazität (''τ = RC''). Bliebe der Entladestrom so stark wie zu Beginn des Vorgänges, wäre der Kondensator nach einer einzigen Zeitkonstante leer. Im ''RC''-Kreis fällt die Spannung und damit auch die Ladung aber nur auf den e-ten Teil ab. |
||
Der elektrische Strom geht infolge des Ohmschen |
Der elektrische Strom geht infolge des Ohmschen Gesetzes ebenfalls exponentiell zurück. Die Leistung im Widerstand fällt sogar mit doppelter Zeitkonstanten ab |
||
:<math>P=UI=P_ae^{-2t/\tau}</math> mit <math>P_a=\frac{U_a^2}{R}</math> |
:<math>P=UI=U_ae^{-t/\tau}I_ae^{-t/\tau}=P_ae^{-2t/\tau}</math> mit <math>P_a=\frac{U_a^2}{R}</math> |
||
In Natur und Technik findet man viele dynamische Vorgänge, die analog zum [[Kondensator entladen|Entladen eines Kondensators]] verlaufen. |
In Natur und Technik findet man viele dynamische Vorgänge, die analog zum [[Kondensator entladen|Entladen eines Kondensators]] verlaufen. |
||
==Kontrollfragen== |
|||
#Wie ändert sich die Kapazität einer Metallkugel, wenn man den Durchmesser verdoppelt? |
|||
#Wie ist die Kapazität definiert? |
|||
#Wie ist ein Kondensator aufgebaut? |
|||
#Welchen Einfluss hat das Dielektrikum auf die Grösse der Kapazität? |
|||
#Wovon hängt die Kapazität eines Plattenkondensators ab? |
|||
#Zwei Platten, die in einem Meter Abstand parallel ausgerichtet sind, sollen einen Kondensator mit der Kapazität von einem Farad bilden. Wie gross muss die Fläche einer Platte gewählt werden? |
|||
#Wie berechnet man die Energie eines Kondensators? |
|||
#Ein Kondensator (Kapazität ''C'') wird über einen Widerstand (''R'') entladen. Wie lange muss man warten, bis die Spannung auf 1% ihres anfänglichen Wertes gesunken ist (ausgedrückt in Zeitkonstanten ''τ = RC'')? |
|||
==Antworten zu den Kontrollfragen== |
|||
#Die Kapazität verdoppelt sich ebenfalls, obwohl die Oberfläche viermal grösser wird. |
|||
#Die Kapazität eines Kondensators ist gleich dem Verhältnis von Ladung auf einem Teil (geflossene Ladung) zu angelegter Spannung. |
|||
#Ein Kondensator besteht aus zwei gut leitenden Teilen (meist Metall) und einer isolierenden Zwischenschicht. |
|||
#Das Dielektrikum isoliert die beiden Teile des Kondensators gegeneinander und schwächt das elektrische Feld ab. |
|||
#Die Kapazität eines Plattenkondensators ist proportional zur Fläche der Platte und umgekehrt proportional zum Abstand der Platten. |
|||
#Jede der beiden Platten müsste eine Fläche von 1.13 10<sup>11</sup> m<sup>2</sup> (2.8 mal die Fläche der Schweiz) aufweisen. |
|||
#Die Energie eines Kondensators ist gleich Ladung mal halbe Spannung (Kapazität halbe mal Spannung im Quadrat). |
|||
#Löst man die Spannungs-Zeit-Funktion <math>U=U_0e^{-\frac{t}{\tau}}</math> nach der Zeit auf, erhält man <math>t=\tau\ln\frac{U_0}{U}</math>, was bei einem Spannungsverhältnis von 1:100 einen Wert von 4.6 ergibt. |
|||
== Materialien == |
|||
*[https://home.zhaw.ch/~mau/Lehre/Skript/ElektrizitaetT.pdf Skript] Seiten 6 und 8 |
|||
*[[Physik - Ein systemdynamischer Zugang für die Sekundarstufe II]] Seiten 58 - 61 |
|||
*[https://cast.switch.ch/vod/clips/7wq10fzp0/link_box Videoaufzeichnung] |
|||
*[http://www.youtube.com/watch?v=Tapq2TxR1o4 Kurzfassung auf Youtube] |
|||
'''[[Physik und Systemwissenschaft in Aviatik]]''' |
|||
[[Kategorie:VorAV]] |
|||
Aktuelle Version vom 6. Oktober 2014, 04:04 Uhr
Elektrische Ladung kann kaum gespeichert werden, weil das von der Ladung erzeugte Feld extrem stark ist. Würde man die Natrium- und Chlorionen von nur einem Gramm Kochsalz trennen und separat auf den Nordpol bzw. dem Südpol der Erde bringen, würden sich diese beiden Teile des Kochsalzes mit 150 N anziehen.
Ladung kann umso besser gespeichert werden, je kleinräumiger und schwächer das zugehörige Feld ist. Elektrische Kondensatoren sind deshalb so gebaut, dass das von der Ladung erzeugte Feld möglich geschwächt und in seiner räumlichen Ausdehnung weitgehend begrenzt wird.
Lernziele
In dieser Vorlesung lernen Sie
- was man in der Elektrodynamik unter einer Kapazität versteht und in welcher Einheit diese gemessen wird
- wie ein Kondensator aufgebaut ist
- wie Kondensatoren im Flüssigkeitsbild darzustellen sind
- wie man die Kapazität eines Platten- und eines Kugelkondensators berechnet
- wie ein zum Kondensator analoges hydraulisches Gerät aussieht
- wie die von Kondensatoren gespeicherte Energie zu berechnen ist
- wie sich Strom und Spannung beim Entladen eines Kondensators über einem Widerstand ändern
Kapazität einer Kugel
In den einführenden Experimenten haben wir isolierte Metallkugeln mit einem an Wolle geriebenen Glasstab geladen oder mit einem Bernsteinstab entladen. Die mit den Kugeln verbundenen Elektrometer zeigten dann das zugehörige Potenzial, die Spannung gegen Erde, an. Nun nimmt eine grosse Kugel bei gleichem Potenzial mehr Ladung auf als eine kleine, d.h. grosse Kugel verfügt über mehr Kapazität als die kleine. In der Elektrodynamik wird die Kapazität analog zur Hydrodynamik definiert: die Kapazität ist gleich dem Verhältnis von gespeicherter Ladung zu der dadurch verursachten Spannung
- [math]C=\frac{Q}{U}[/math]
Die Kapazität misst man in Coulomb pro Volt oder Farad (F, benannt nach Michael Faraday)
- 1 F = 1 C/V = 1 As/V
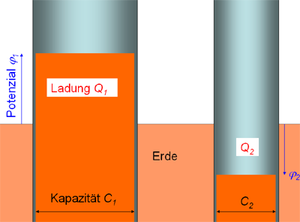
Die Ladung auf einer Metallkugel (es könnte auch ein anders geformter Körper sein) erzeugt im Aussenraum ein elektrisches Feld, das durch die Ladungen der umgebenden Körper, speziell der Erdoberfläche, begrenzt wird. Die Spannung ist deshalb gegen die Erde zu messen (Potenzial). Verändert man die Lage der umgebenden Körper, beeinflusst dies das elektrische Feld und damit auch das Potenzial der Kugel. Befindet sich die Metallkugel (Radius r) weit weg von allen leitfähigen Körperoberflächen, lässt sich die zugehörige Kapazität mit einer einfachen Formel beschreiben
- [math]C=4\pi\varepsilon_0 r[/math]
Epsilon steht für die elektrische Feldkonstante (ε0 = 8.854 10-12 F/m). Interessanterweise nimmt die Kapazität einer Kugel nicht proportional zum Volumen oder zur Oberfläche sondern linear mit dem Radius zu. Um dies zu zeigen, müsste man mehr über die Gesetze, welche das elektromagnetische Feld beschreiben, wissen.
Die Zusammenhänge zwischen Ladung, Kapazität und Potenzial lassen sich sehr schön im Flüssigkeitsbild darstellen. Stellt man sich die Ladung als Flüssigkeit, die Körper als zylindrische Gefässe und die Kapazität als Querschnitt dieser Gefässe vor, verwandelt sich das Potenzial in eine Füllhöhe. Die Ladung, die als Kapazität mal Potenzial geschrieben werden kann, erscheint dann im Flüssigkeitsbild als Grundfläche mal Höhe.
Kondensatoren
Umhüllt man eine elektrisch geladene Metallkugel mit einer zweiten, die geerdet ist, fliesst von der zweiten Kugel gleich viel Ladung weg, wie auf der ersten gespeichert ist. Dieses Phänomen, Influenz genannt, führt dazu, dass ausserhalb der beiden Kugeln kein elektrisches Feld mehr nachzuweisen ist. Mit der zweiten Kugelschale, Abschirmung genannt, erreicht man zwei Dinge: erstens stört das eingeschlossene Feld keine andern Systeme im Aussenraum und zweitens wird das elektrische Feld räumlich begrenzt, was die Kapazität beträchtlich erhöht.
Die Kapazität eines Kugelkondensators (zwei konzentrische Kugeln mit je einem Anschluss) ist gleich
- [math]C=4\pi\varepsilon_0\frac{r_2r_1}{r_2-r_1}[/math]
wobei mit r1 der Aussenradius der Innenkugel und mit r2 der Innenradius der Aussenkugel gemeint ist.
Die elektrische Ladung sitzt auf der Innenkugel aussen und auf der Aussenkugel innen. Der Grund dafür ist in der Leitfähigkeit der Kugelschalen zu suchen. Würde das elektrische Feld in das Metall eindringen, würde es dort gemäss dem Ohmschen Gesetz einen Strom antreiben. Folglich darf sich das elektrische Feld nur zwischen den Metallteilen ausdehnen und die Ladungen, die dieses Feld aufbauen, müssen auf der Metalloberfläche sitzen.
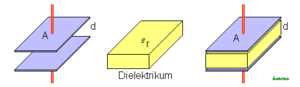
Je kleiner der Spalt zwischen den beiden Kugeln (r2 - r1), desto kürzer das Feld, desto kleiner die Spannung bei gegebener Ladung und um so grösser die Kapazität. Wählt man den Spalt immer enger, darf die Spannung zwischen den beiden Kugeln nicht zu gross werden. Sonst würden die Elektronen durch das starke Feld aus dem negativ geladenen Teil heraus gerissen und gegen den positiven geschleudert. Um solche Kurzschlussströme zu verhindern, füllt man den Raum zwischen den beiden Teilen des Kondensators mit einem isolierenden Material, dem Dielektrikum, auf. Das Dielektrikum ermöglicht nicht nur eine höhere Spannung, sondern schwächt auch noch das durch die Ladung erzeugte Feld ab. Diese Schwächung des Feldes durch das Dielektrikum wird mit der Dielektrizitätszahl beschrieben. Nun nennt man das Produkt aus elektrischer Feldkonstante (ε0) und Dielektrizitätszahl (εr) Dielektrizitätskonstante (ε)
- [math]\varepsilon=\varepsilon_r\varepsilon_0[/math]
Diese Konstruktion mit elektrischer Feldkonstante, Dielektrizitätszahl und Dielektrizitätskonstante mag etwas kompliziert tönen, hat aber den Vorteil, dass die Kapazitäten der Kondensatoren einfach zu berechnen sind. Man nimmt die im Vakuum berechnete Kapazität und schreibt statt ε0 einfach nur ε. So lautet die Formel für den Kugelkondensator mit Dielektrikum
- [math]C=4\pi\varepsilon\frac{r_2r_1}{r_2-r_1}[/math]
Wählt man die innere Kugel des Kugelkondensators sehr gross und die äussere nur ein klein wenig grösser, wird das elektrische Feld im Zwischenraum analog dem Gravitationsfeld der Erde ziemlich homogen. Ein kleines Stück dieses Kugelkondensators bildet dann einen Plattenkondensator mit der Kapazität
- [math]C=\varepsilon\frac{A}{d}[/math]
wobei A für die Fläche der einen Platte und d für den Abstand zwischen den Platten steht.
hydroelektrische Analogie
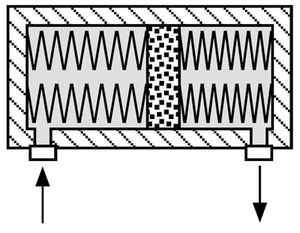
Der Kondensator speichert netto keine elektrische Ladung, weil sich die Ladung auf seinen beiden Teilen zu Null kompensiert. Das elektrische Feld, das beim Laden des Kondensators aufgebaut wird, erstreckt sich denn auch nur zwischen den beiden Metallflächen (bei neueren Kondensatoren nur über eine Oxidschicht oder eine Schicht aus wenigen Molekülen). Fliesst nun in einem der beiden Anschlüsse ein elektrischer Strom zu, geht im andern Anschluss genau der gleich starke Strom weg. Von aussen könnte man meinen, dass der elektrische Strom einfach nur so durchfliesst. Doch mit der geflossenen Ladung Q steigt auch die Spannung U über den beiden Anschlüssen (mit Q meint man immer die geflossene oder auf einem Teil des Kondensators gespeicherte Ladung).
Das hydraulische Analogon ist nebenstehend skizziert. Pumpt man die Flüssigkeit mit dem Volumen ΔV auf der einen Seite hinein, steigt der Druckunterschied zwischen den beiden Anschlüssen um Δp. Das Verhältnis zwischen ΔV und Δp ist die hydraulische Kapazität. Die hydraulische Kapazität ist konstant, solange sich die Federn linear verhalten. Das Gesamtvolumen dieses hydraulischen Speichers bleibt wie die elektrische Ladung des Kondensators konstant: was auf der einen Seite hinein kommt, geht auf der andern augenblicklich wieder weg.
Energiespeicher
Der Begriff Kapazität, welcher das Verhältnis zwischen geflossener Ladung und Änderung der Spannung beschreibt, kann auch direkt auf den Strom umdefiniert werden. Dazu formulieren wir die Bilanz bezüglich der einen Hälfte des Kondensators (Strom ist gleich Änderungsrate der Ladung) und ersetzen die Ladung durch Kapazität mal Spannung. Die Änderungsrate der Ladung wird so durch Kapazität mal Änderungsrate der Spannung ersetzt
- [math]I=\dot Q=C\dot U[/math]
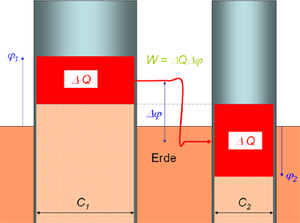
Fliesst nun in einem Draht des Kondensators ein konstanter Strom zu, steigt die Spannung linear in der Zeit. Damit nimmt die Leistung ebenfalls kontinuierlich zu. Die vom Stromkreis auf das elektrische Feld des Kondensators übertragene Energie ist deshalb gleich mittlere Spannung mal geflossene Ladung oder halbe Endspannung mal geflossene Ladung
- [math]W=\frac{U}{2}Q=\frac{C}{2}U^2=\frac{Q^2}{2C}[/math]
Wieder hilft uns das Flüssigkeitsbild den Sachverhalt besser zu verstehen. Denken wir uns den einen Teil des Kondensators geerdet, dann erscheint der andere Teil im Flüssigkeitsbild als Topf. Um Flüssigkeit aus einem grossen See in ein Reservoir zu pumpen, muss die am Schluss im Reservoir vorhandene Flüssigkeit (Ladung Q) um die halbe Höhe (mittlere Spannung) angehoben werden.
Beispiel:
Ein Kondensator mit der Kapazität C1, der bis auf die Spannung U1 aufgeladen worden ist, wird mit einem zweiten Kondensator (Kapazität C2, Spannung U2) verbunden. Wie sieht der Endzustand aus und wie viel Energie wird dissipert? Diese Aufgabe ist mit Hilfe des Flüssigkeitsbildes spielend leicht zu beantworten. Wieder denken wir uns die eine Seite der Kondensatoren geerdet. Dann können die beiden andern Teile als Töpfe und die angelegte Spannung als Füllhöhe dargestellt werden. Der Ausgleichsvorgang ist im nebenstehenden Bild dargestellt. Die Spannung, die schlussendlich an beiden Kondensatoren anliegt, ist direkt dem Bild zu entnehmen. Die dissipierte Energie ist dann gleich geflossene Ladung mal mittlere Fallhöhe.
RC-Glied
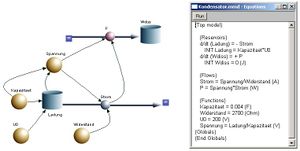
Schliesst man einen geladenen Kondensator (Kapazität C) über einen Widerstand R kurz, entlädt sich der Kondensator vollständig und die von ihm gespeicherte Energie wird im Widerstand dissipiert. Das Systemdiagramm dieses Vorgangs lässt sich mit etwas Übung schnell zeichnen
- Ladungsbilanz bezüglich des nicht geerdeten Teils
- Potenzial mit Hilfe der Kapazität rechnen
- Potenzial treibt den Strom entsprechend des Widerstandes
- Leistung und Energie als zweite Ebene (Buchhaltung) hinzufügen
Die Gleichungen für dieses System findet man im Fenster "Equations" von BerkeleyMadonna. Lässt man für die Beschreibung die Energiebetrachtung weg, kann der Rest in eine einzige Gleichung umgeformt werden
- [math]U+RC\dot U=0[/math]
Diese Gleichung hat eine einfache Lösung. Lädt man den Kondensator vorher auf Ua auf, folgt der zeitliche Verlauf der Spannung einer Exponentialkurve
- [math]U=U_ae^{-t/\tau}[/math]
τ ist die Zeitkonstante. Nun ist der Wert der Zeitkonstanten gleich dem Produkt aus Widerstand und Kapazität (τ = RC). Bliebe der Entladestrom so stark wie zu Beginn des Vorgänges, wäre der Kondensator nach einer einzigen Zeitkonstante leer. Im RC-Kreis fällt die Spannung und damit auch die Ladung aber nur auf den e-ten Teil ab.
Der elektrische Strom geht infolge des Ohmschen Gesetzes ebenfalls exponentiell zurück. Die Leistung im Widerstand fällt sogar mit doppelter Zeitkonstanten ab
- [math]P=UI=U_ae^{-t/\tau}I_ae^{-t/\tau}=P_ae^{-2t/\tau}[/math] mit [math]P_a=\frac{U_a^2}{R}[/math]
In Natur und Technik findet man viele dynamische Vorgänge, die analog zum Entladen eines Kondensators verlaufen.
Kontrollfragen
- Wie ändert sich die Kapazität einer Metallkugel, wenn man den Durchmesser verdoppelt?
- Wie ist die Kapazität definiert?
- Wie ist ein Kondensator aufgebaut?
- Welchen Einfluss hat das Dielektrikum auf die Grösse der Kapazität?
- Wovon hängt die Kapazität eines Plattenkondensators ab?
- Zwei Platten, die in einem Meter Abstand parallel ausgerichtet sind, sollen einen Kondensator mit der Kapazität von einem Farad bilden. Wie gross muss die Fläche einer Platte gewählt werden?
- Wie berechnet man die Energie eines Kondensators?
- Ein Kondensator (Kapazität C) wird über einen Widerstand (R) entladen. Wie lange muss man warten, bis die Spannung auf 1% ihres anfänglichen Wertes gesunken ist (ausgedrückt in Zeitkonstanten τ = RC)?
Antworten zu den Kontrollfragen
- Die Kapazität verdoppelt sich ebenfalls, obwohl die Oberfläche viermal grösser wird.
- Die Kapazität eines Kondensators ist gleich dem Verhältnis von Ladung auf einem Teil (geflossene Ladung) zu angelegter Spannung.
- Ein Kondensator besteht aus zwei gut leitenden Teilen (meist Metall) und einer isolierenden Zwischenschicht.
- Das Dielektrikum isoliert die beiden Teile des Kondensators gegeneinander und schwächt das elektrische Feld ab.
- Die Kapazität eines Plattenkondensators ist proportional zur Fläche der Platte und umgekehrt proportional zum Abstand der Platten.
- Jede der beiden Platten müsste eine Fläche von 1.13 1011 m2 (2.8 mal die Fläche der Schweiz) aufweisen.
- Die Energie eines Kondensators ist gleich Ladung mal halbe Spannung (Kapazität halbe mal Spannung im Quadrat).
- Löst man die Spannungs-Zeit-Funktion [math]U=U_0e^{-\frac{t}{\tau}}[/math] nach der Zeit auf, erhält man [math]t=\tau\ln\frac{U_0}{U}[/math], was bei einem Spannungsverhältnis von 1:100 einen Wert von 4.6 ergibt.
Materialien
- Skript Seiten 6 und 8
- Physik - Ein systemdynamischer Zugang für die Sekundarstufe II Seiten 58 - 61
- Videoaufzeichnung
- Kurzfassung auf Youtube