Spannungsteiler mit Induktivität: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 21. Dezember 2006, 11:50 Uhr

System

Ein Potentiometer wird mit einer supraleitenden Spule (reine Induktivität) statt mit einem Lastwiderstand verbunden. Unmittelbar nach dem Zuschalten der Spannungsquelle fliesst der Strom nur über das Potentiometer. Weil die Spannung über dem zweiten Teil des Potentiometers (R₂) gleich der Spannung über der Spule ist, beginnt die Stärke des durch die Spule fliessenden Stromes zu wachsen. Nach längerer Zeit fliesst der Strom nur noch durch den Widerstand R₁ und die Spule.

Systemmodell

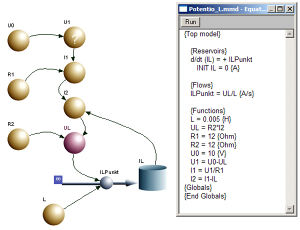
Die systemdynamische Modellierung geht von der Bilanz einer mengenartigen Grösse aus. Weil in diesem System nur Ströme fliessen und kein Ladungsspeicher vorhanden ist, modellieren wir zuerst die Induktivität (sihe auch Lineare passive Zweipole):

Die Spannung über dem Widerstand (U₂) ist gleichzeitig der Antrieb (U_L) für die Änderungsrate der Stromstärke bei der Induktivität (U_L = L dI_L/dt)
die Spannung über der Induktivität und dem Widerstand 2 (U₂ = U_L ) ist gleich Stromstärke I₂ mal zugehöriger Widerstand (R₂)
die Stromstärke durch Widerstand 2 (I₂) ist gleich Stromstärke durch Widerstand 1 (I₁) minus die Stärke des durch die Spule fliessenden Stromes (I_L).
die Stromstärke durch Widerstand 1 (I₁) ist gleich der Differenz der angelegten Spannung (U₀) und der Spannung über dem Widerstand 2 (U₂) dividiert durch den Widerstand 1 (R₁).

Bei der Modellierung der Beziehung U₁ = U₀ - U_L meldet das Modellierungswerkzeug BerkeleyMadonna Arc connection. Eine Kreisverbindung mit reinen Wirkpfeilen (Arcs) ist nicht zulässig, weil eine solche algebraische Schleife (algebraic loop) keine Wirkkette mehr darstellt, entlang derer das Programm das Modell integrieren kann. Mathematisch betrachtet bildet eine algebraische Schleife ein Gleichungssystem, das hier von Hand zu lösen ist

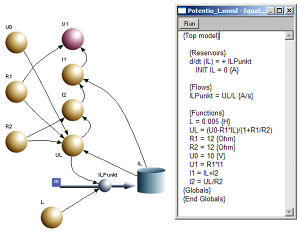
Knotensatz (Bilanz): [math]I_1 = I_2 + I_L[/math]
Addition der Spannungen: [math]U_0 = U_1 + U_2[/math]
Ohmsches Gesetz 1: [math]U_1 = R_1 I_1[/math]
Ohmsches Gesetz 2: [math]U_2 = R_2 I_2[/math]

Löst man dieses Gleichungssystem nach der gesuchten Grösse U₂ mit den Eingangsgrössen U₀ und I_L auf, erhält man

[math]U_L = U_2 = \frac {U_0 - R_1I_L}{1 + \frac {R_1}{R_2}}[/math]

Diese Gleichung liefert die Verbindung zwischen der Stromstärke durch die Spule und der Spannung über der Spule. Die andern Grössen sind dann "rückwärts" zu berechnen.

Die Simulatoren der höheren Programmmiersprache Modelica sind in der Lage, algebraische Schleifen automatisch zu lösen.

Simulation

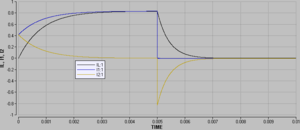
Das nebenstehend abgebildete Diagramm zeigt den Verlauf der Strom-Zeit-Funktionen nach dem Einschalten. Nach 5 ms wird die Verbindung zur Spannungsquelle wieder unterbrochen. Die Induktivität treibt dann den Strom durch den Widerstand 2 (R₂) im Kreis herum, bis die magnetische Energie der Spule dissipiert ist. Die Induktivität widersetzt sich jeder Veränderung der Stromstärke durch eine Art Trägheit. Diese Trägheit widerspiegelt das Energiespeicher-Vermögen des magnetischen Feldes: solange die Stromstärke betragsmässig wächst, verhält sich die Induktivität wie ein Verbraucher; soll der Betrag der Stromstärke vermindert werden, wirk die Induktivität wie eine Quelle.

Das Abschalten der externen Spannungsquelle modelliert man bei U_L:

if time < 0.005 then (U0-R1*IL)/(1+R1/R2) else -R2* IL

Solch plötzliche Veränderungen in der mathematischen Struktur eines Modells (strukturvariables System) können zu numerischen Problemen führen, wenn sie zu viele solche Änderungen zu oft auftreten.

Energiebetrachtung

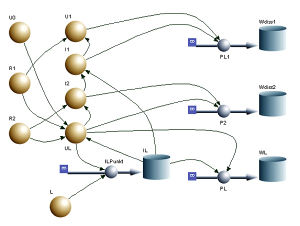
Die Prozessleistung ist gleich Spannung mal Stromstärke. Handelt es sich um einen Widerstand, wird die ganze Leistung dissipiert. Bei der Induktivität wird die Prozessleistung vom Magnetfeld aufgenommen

[math]\dot W_{Magnetfeld} = P = U_L I_L[/math]

Integriert man die Prozessleistung über die Zeit, erhält man bei den beiden Widerständen die disspierte Energie und bei einer Induktivität die Änderung der im Magnetfeld gespeicherten Energie. Das Bild zeigt das Energie-Zeit-Diagramm für die drei Elemente.

@@ Zeile 4: / Zeile 4: @@
 ==Systemmodell==
 [[Bild:Spannungsteiler_mit_Induktivitaet_SD.jpg|thumb|Systemdiagramm mit algebraischer Schleife]]
-Die [[Systemdiagramm|systemdynamische Modellierung]] geht von der Bilanz einer [[Primärgrösse|mengenartigen Grösse]] aus. Weil in diesem System nur Ströme fliessen und kein Ladungsspeicher vorhanden ist, modellieren wir zuerst die Induktivität(''L'') ([[Lineare passive Zweipole]]):
+Die [[Systemdiagramm|systemdynamische Modellierung]] geht von der Bilanz einer [[Primärgrösse|mengenartigen Grösse]] aus. Weil in diesem System nur Ströme fliessen und kein Ladungsspeicher vorhanden ist, modellieren wir zuerst die Induktivität (sihe auch [[Lineare passive Zweipole]]):
 *Die Spannung über dem Widerstand (''U<sub>2</sub>'') ist gleichzeitig der Antrieb (''U<sub>L</sub>'') für die Änderungsrate der Stromstärke bei der Induktivität (''U<sub>L</sub> = L dI<sub>L</sub>/dt'')
 *die Spannung über der Induktivität und dem Widerstand 2 (''U<sub>2</sub>'' = ''U<sub>L</sub>'' ) ist gleich Stromstärke ''I<sub>2</sub>'' mal zugehöriger Widerstand (''R<sub>2</sub>'')
@@ Zeile 26: / Zeile 26: @@
 ==Simulation==
-[[Bild:Spannungsteiler_mit_Kapazitaet_I.png|thumb|Strom-Zeit-Verlaub]]
+[[Bild:Spannungsteiler_mit_Induktivitaet_I.png|thumb|Strom-Zeit-Verlaub]]
-Das nebenstehend abgebildete Diagramm zeigt den Verlauf der Strom-Zeit-Funktion nach dem Einschalten. Nach 200 s wird die Verbindung zur Spannungsquelle wieder unterbrochen. Anfänglich fliesst der Strom durch den Widerstand 1 (''R<sub>1</sub>'') und den Kondensator, wobei dessen Stärke nur durch den Widerstand 1 begrenzt wird. Je mehr Strom bezüglich des Kondensators (''I<sub>C</sub>'') geflossen ist, umso mehr steigt die Spannung über dem Kondensator und damit auch über dem Widerstand 2. Folglich fällt die Stromstärke durch Widerstand 1 (''I<sub>1</sub>'') ab und die durch Widerstand 2 (''I<sub>2</sub>'') steigt. Weil immer mehr Strom durch Widerstand 2 fliesst, geht weniger durch den Kondensatorzweig (''I<sub>C</sub>'').
+Das nebenstehend abgebildete Diagramm zeigt den Verlauf der Strom-Zeit-Funktionen nach dem Einschalten. Nach 5 ms wird die Verbindung zur Spannungsquelle wieder unterbrochen. Die Induktivität treibt dann den Strom durch den Widerstand 2 (''R<sub>2</sub>'') im Kreis herum, bis die magnetische Energie der Spule [[Dissipation|dissipiert]] ist. Die Induktivität widersetzt sich jeder Veränderung der Stromstärke durch eine Art Trägheit. Diese Trägheit widerspiegelt das Energiespeicher-Vermögen des magnetischen Feldes: solange die Stromstärke betragsmässig wächst, verhält sich die Induktivität wie ein Verbraucher; soll der Betrag der Stromstärke vermindert werden, wirk die Induktivität wie eine Quelle.
+Das Abschalten der externen Spannungsquelle modelliert man bei ''U<sub>L</sub>'':
-Nachdem die Verbindung zur Spannungsquelle unterbrochen wird, [[Kondensator entladen|entlädt]] sich der Kondensator über den Widerstand 2. Die Stromstärke durch Widerstand 1 (''I<sub>1</sub>'') ist sofort gleich Null, die durch Widerstand 2 (''I<sub>2</sub>'') geht exponentiell gegen Null. Die Stromstärke im Kondensatorzweig (''I<sub>C</sub>'') kehrt das Vorzeichen um und hat danach immer den gleichen Betrag wie die Stromstärke durch Widerstand 2.
+if time < 0.005 then (U0-R1*IL)/(1+R1/R2) else -R2* IL
-==Energiebetrachtung==
-[[Bild:Spannungsteiler_mit_Kapazitaet_SD_W.jpg|thumb|Systemdiagramm mit Energiebetrachtung]]
-Die Prozessleistung ist gleich Spannung mal Stromstärke. Handelt es sich um einen Widerstand, wird die ganze Leistung [[Dissipation|dissipiert]]. Die Leistung kann dann auch als Widerstand mal Stromstärke im Quadrat geschrieben werden.
+Solch plötzliche Veränderungen in der mathematischen Struktur eines Modells (strukturvariables System) können zu numerischen Problemen führen, wenn sie zu viele solche Änderungen zu oft auftreten.
-Integriert man die Prozessleistung über die Zeit erhält man bei Widerständen die disspierte Energie und bei einem Kondensator die Änderung der gespeicherten Energie.
+==Energiebetrachtung==
+[[Bild:Spannungsteiler_mit_Induktivitaet_SD_W.jpg|thumb|Systemdiagramm mit Energiebetrachtung]]
+Die Prozessleistung ist gleich Spannung mal Stromstärke. Handelt es sich um einen Widerstand, wird die ganze Leistung [[Dissipation|dissipiert]]. Bei der Induktivität wird die Prozessleistung vom Magnetfeld aufgenommen
+<math>\dot W_{Magnetfeld} = P = U_L I_L</math>
-[[Bild:Spannungsteiler_mit_Kapazitaet_W.png|thumb|Energie-Zeit-Funktion]]
-[[Kategorie:Elektro]] [[Kategorie:ElektroMod]]
-. Nach längerer Zeit fliesst der Strom nur noch durch das Potentiometer, das die angelegte Spannung im Verhältnis der beiden Widerstände teilt.
+Integriert man die Prozessleistung über die Zeit, erhält man bei den beiden Widerständen die disspierte Energie und bei einer Induktivität die Änderung der im Magnetfeld gespeicherten Energie. Das Bild zeigt das Energie-Zeit-Diagramm für die drei Elemente.
-Entfernt man die Spannungsquelle, entlädt sich der Kondensator über dem zweiten Teil des Potentiometers (''R<sub>2</sub>''). Stromstärke und Spannung nehmen entsprechend eines [[Kondensator entladen|Entladevorganges]] eines Kondensators ab.
+[[Bild:Spannungsteiler_mit_Induktivitaet_W.png|thumb|Energie-Zeit-Funktion]]
-[[Kategorie:Elektro]] [[Kategorie:ElektroMod]]
+[[Kategorie:Elektro]] [[Kategorie:Modelle]] [[Kategorie:ElektroMod]]