Staurohr: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Bild:Staurohr.png|thumb|Staurohr nach Prandtl]] |
[[Bild:Staurohr.png|thumb|Staurohr nach Prandtl]] |
||
Das Staurohr ist ein Pitotrohr (benannt nach Henri Pitot; engl. pitot tube) kombiniert mit einer zusätzlichen statischen Drucksonde. Ein Pitotrohr ist ein gerades oder L-förmiges, einseitig offenes Rohr zur Messung des Gesamtdruckes (Summe aus statischem Druck und Staudruck) von Flüssigkeiten oder Gasen. Das Prandtl'sche Staurohr wird in der Fliegerei zur Geschwindigkeitsmessung verwendet. |
Das Prandtl'sche Staurohr ist ein Pitotrohr (benannt nach Henri Pitot; engl. pitot tube) kombiniert mit einer zusätzlichen statischen Drucksonde. Ein Pitotrohr ist ein gerades oder L-förmiges, einseitig offenes Rohr zur Messung des Gesamtdruckes (Summe aus statischem Druck und Staudruck) von Flüssigkeiten oder Gasen. Das Prandtl'sche Staurohr wird in der Fliegerei zur Geschwindigkeitsmessung verwendet. |
||
Das Staurohr vergleicht den Druck im Staupunkt (an der Spitze des Rohres) mit dem Druck des ungehindert vorbeifliessenden [[Fluid]]s. Geht man nun davon aus, dass die Strömung um das Staurohr herum nahezu eine [[Potenzialströmung]] ist, dürfen die beiden Messpunkte mit Hilfe des [[Gesetz von Bernoulli|Gesetzes von Bernoulli]] verglichen werden |
Das Prandtl'sche Staurohr vergleicht den Druck im Staupunkt (an der Spitze des Rohres) mit dem Druck des praktisch ungehindert vorbeifliessenden [[Fluid]]s. Geht man nun davon aus, dass die Strömung um das Staurohr herum nahezu eine [[Potenzialströmung]] ist, dürfen die beiden Messpunkte mit Hilfe des [[Gesetz von Bernoulli|Gesetzes von Bernoulli]] verglichen werden |
||
:<math>\frac {\rho}{2} v_1^2 + \rho g h_1 + p_1 = \frac {\rho}{2} v_2^2 + \rho g h_2 + p_2</math> |
:<math>\frac {\rho}{2} v_1^2 + \rho g h_1 + p_1 = \frac {\rho}{2} v_2^2 + \rho g h_2 + p_2</math> |
||
Da der Höhenunterschied zwischen den beiden Punkten vernachlässigt werden kann und die Geschwindigkeit im Staupunkt (1) verschwindet, ist der Druck im Staupunkt um die Dichte der kinetischen Energie des vorbeiströmenden Fluids grösser als im Punkt 2 |
Da der Höhenunterschied zwischen den beiden Punkten vernachlässigt werden kann und die Geschwindigkeit im Staupunkt (Punkt 1) verschwindet, ist der Druck im Staupunkt um die Dichte der kinetischen Energie des vorbeiströmenden Fluids grösser als im Punkt 2 |
||
:<math>p_1 = p_2 + \frac {\rho}{2} v_2^2</math> |
:<math>p_1 = p_2 + \frac {\rho}{2} v_2^2</math> |
||
| Zeile 15: | Zeile 15: | ||
Der Index 2 ist hier weggelassen worden, weil die Geschwindigkeit im Punkt 2 ziemlich genau der zu messenden Anströmung entspricht. |
Der Index 2 ist hier weggelassen worden, weil die Geschwindigkeit im Punkt 2 ziemlich genau der zu messenden Anströmung entspricht. |
||
[[Kategorie:Hydro]] [[Kategorie:OffSys]] |
|||
Aktuelle Version vom 26. Februar 2007, 15:12 Uhr
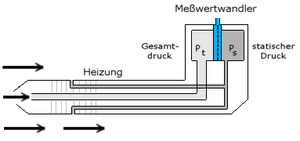
Das Prandtl'sche Staurohr ist ein Pitotrohr (benannt nach Henri Pitot; engl. pitot tube) kombiniert mit einer zusätzlichen statischen Drucksonde. Ein Pitotrohr ist ein gerades oder L-förmiges, einseitig offenes Rohr zur Messung des Gesamtdruckes (Summe aus statischem Druck und Staudruck) von Flüssigkeiten oder Gasen. Das Prandtl'sche Staurohr wird in der Fliegerei zur Geschwindigkeitsmessung verwendet.
Das Prandtl'sche Staurohr vergleicht den Druck im Staupunkt (an der Spitze des Rohres) mit dem Druck des praktisch ungehindert vorbeifliessenden Fluids. Geht man nun davon aus, dass die Strömung um das Staurohr herum nahezu eine Potenzialströmung ist, dürfen die beiden Messpunkte mit Hilfe des Gesetzes von Bernoulli verglichen werden
- [math]\frac {\rho}{2} v_1^2 + \rho g h_1 + p_1 = \frac {\rho}{2} v_2^2 + \rho g h_2 + p_2[/math]
Da der Höhenunterschied zwischen den beiden Punkten vernachlässigt werden kann und die Geschwindigkeit im Staupunkt (Punkt 1) verschwindet, ist der Druck im Staupunkt um die Dichte der kinetischen Energie des vorbeiströmenden Fluids grösser als im Punkt 2
- [math]p_1 = p_2 + \frac {\rho}{2} v_2^2[/math]
Löst man diese Gleichung nach der Geschwindigkeit auf, erhält man
- [math]v = \sqrt {\frac {2 \Delta p}{\rho}}[/math]
Der Index 2 ist hier weggelassen worden, weil die Geschwindigkeit im Punkt 2 ziemlich genau der zu messenden Anströmung entspricht.