Schiefe Ebene und Gegengewicht: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Bild:schiefe_Ebene_Gegengewicht.png|thumb|Klotz mit Gegengewicht]] |
[[Bild:schiefe_Ebene_Gegengewicht.png|thumb|Klotz mit Gegengewicht]] |
||
Ein auf einer schiefen Ebene (Neigungswinkel 30°) liegender Klotz ([[Masse]] 6 kg) ist über ein Seil und eine Umlenkrolle mit einem "Gegengewicht", einem Körper mit einer Masse von 4 kg, verbunden. Die Gleitreibungszahl für die Grenzschicht Klotz-Ebene beträgt 0. |
Ein auf einer schiefen Ebene (Neigungswinkel 30°) liegender Klotz ([[Masse]] 6 kg) ist über ein Seil und eine Umlenkrolle mit einem "Gegengewicht", einem Körper mit einer Masse von 4 kg, verbunden. Die Gleitreibungszahl für die Grenzschicht Klotz-Ebene beträgt 0.1. Umlenkrolle und Seil haben keine Masse und arbeiten reibungsfrei. |
||
#[[Freischneiden|Schneiden]] Sie beide Körper frei, zeichnen Sie also die auf jeden der beiden Körper einwirkenden [[Kraft|Kräfte]] mit je einer separaten Farbe ein. |
#[[Freischneiden|Schneiden]] Sie beide Körper frei, zeichnen Sie also die auf jeden der beiden Körper einwirkenden [[Kraft|Kräfte]] mit je einer separaten Farbe ein. |
||
#Führen Sie für beide Körper |
#Führen Sie für beide Körper ein getrenntes Koordinatensystem ein und formulieren Sie für beide Systeme die [[Impulsbilanz]] in der Form des [[Grundgesetz der Mechanik|Grundgesetzes der Mechanik]]. |
||
#Berechnen Sie die Beschleunigung des Klotzes und die Grösse der auf den Klotz einwirkenden Seilkraft. |
#Berechnen Sie die Beschleunigung des Klotzes und die Grösse der auf den Klotz einwirkenden Seilkraft. |
||
#Was haben die Impulsänderunsraten der beiden Körper miteinander zu tun? |
#Was haben die Impulsänderunsraten der beiden Körper miteinander zu tun? |
||
#Wie könnte man die Beschleunigung des Klotzes auch noch rechnen? |
|||
'''Hinweis und Kommentar:''' Problemstellungen dieser Art ([[schiefe Ebene]], [[Atwoodsche Fallmaschine]], [[Flaschenzug|Flaschenzüge]]) sind beliebte Objekte der [[Schulphysik]], eignen sich aber kaum als einführende Beispiele für den [[Physik der dynamischen Systeme|systemdynamischen Zugang zur Physik]]. Es ist aber auch ein offenes Geheimnis, dass zu viele Physiklehrer nicht in der Lage sind, solche Aufgaben professionell, d.h. im Sinne der [[technische Mechanik|technischen Mechanik]], zu lösen. |
|||
| ⚫ | |||
| ⚫ | *Man |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
'''Hinweis und Kommentar:''' |
|||
| ⚫ | |||
*Problemstellungen wie die Klötze auf der [[schiefe Ebene|schiefen Ebene]], die [[Atwoodsche Fallmaschine]] oder der [[Flaschenzug]] eignen sich kaum als einführende Beispiele für den [[Physik der dynamischen Systeme|systemdynamischen Zugang zur Physik]]. Bezeichnenderweise sind denn auch die Lösungen, die man in Büchern und an den Wandtafeln vieler Schulen findet, durchsetzt mit fehlerhaften Überlegungen und inkonsistenten Annahmen. Eine korrekte Schlussformel ist noch lange kein Indiz für die korrekte Lösung eines Problems. Den Lehrern, welche in der Netwonschen [[Punktmechanik]] immer noch den Königsweg zum tieferen Verständnis der Physik sehen, sei die hier aufgeführte Lösung ins Stammbuch geschrieben. |
|||
| ⚫ | |||
| ⚫ | **Man zeichnet alle an der Problemstellung beteiligten ([[starrer Körper|starren]]) Körper einzeln auf und markiert alle auf die Körper einwirkenden [[Kraft|Kräfte]] mit je einem Pfeil. Um die Tatsache, dass Kräfte nur attributive Grössen ([[Impulsstrom|Impulsströme]] und [[Impulsquelle|Impulsquellen]] bezüglich eines bewusst ausgewählten Systems) sind, zu betonen, verwende man für jeden Körper eine andere Farbe. |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
'''[[Lösung zu Schiefe Ebene und Gegengewicht|Lösung]]''' |
'''[[Lösung zu Schiefe Ebene und Gegengewicht|Lösung]]''' |
||
Aktuelle Version vom 24. März 2007, 11:57 Uhr
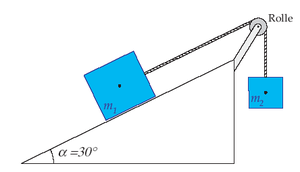
Ein auf einer schiefen Ebene (Neigungswinkel 30°) liegender Klotz (Masse 6 kg) ist über ein Seil und eine Umlenkrolle mit einem "Gegengewicht", einem Körper mit einer Masse von 4 kg, verbunden. Die Gleitreibungszahl für die Grenzschicht Klotz-Ebene beträgt 0.1. Umlenkrolle und Seil haben keine Masse und arbeiten reibungsfrei.
- Schneiden Sie beide Körper frei, zeichnen Sie also die auf jeden der beiden Körper einwirkenden Kräfte mit je einer separaten Farbe ein.
- Führen Sie für beide Körper ein getrenntes Koordinatensystem ein und formulieren Sie für beide Systeme die Impulsbilanz in der Form des Grundgesetzes der Mechanik.
- Berechnen Sie die Beschleunigung des Klotzes und die Grösse der auf den Klotz einwirkenden Seilkraft.
- Was haben die Impulsänderunsraten der beiden Körper miteinander zu tun?
Hinweis und Kommentar:
- Problemstellungen wie die Klötze auf der schiefen Ebene, die Atwoodsche Fallmaschine oder der Flaschenzug eignen sich kaum als einführende Beispiele für den systemdynamischen Zugang zur Physik. Bezeichnenderweise sind denn auch die Lösungen, die man in Büchern und an den Wandtafeln vieler Schulen findet, durchsetzt mit fehlerhaften Überlegungen und inkonsistenten Annahmen. Eine korrekte Schlussformel ist noch lange kein Indiz für die korrekte Lösung eines Problems. Den Lehrern, welche in der Netwonschen Punktmechanik immer noch den Königsweg zum tieferen Verständnis der Physik sehen, sei die hier aufgeführte Lösung ins Stammbuch geschrieben.
- In der technischen Mechanik geht man zur Lösung der Probleme nach einem einfach strukturierten Rezept vor:
- Man zeichnet alle an der Problemstellung beteiligten (starren) Körper einzeln auf und markiert alle auf die Körper einwirkenden Kräfte mit je einem Pfeil. Um die Tatsache, dass Kräfte nur attributive Grössen (Impulsströme und Impulsquellen bezüglich eines bewusst ausgewählten Systems) sind, zu betonen, verwende man für jeden Körper eine andere Farbe.
- Die einmal eingezeichneten Kräfte auf die verschiedenen Körper gehören unterschiedlichen Vektorrräumen an. Also darf man jedem Körper ein eigenes Koordinatensystem zuordnen. Bei zwangsweisen geführten Körpern sollte die eine Achse des Koordinatensystems in Bewegungsrichtung zeigen.
- Nun formuliert man für jeden Körper bezüglich des zugehörigen Koordinatensystems die Impulsbilanz in Form des Grundgesetzes der Mechanik.
- Die Verbindung zwischen den einzelnen Körper erfolgt in der Regel über Seile. Wieso die Seilkräfte auf die beiden Körper betragsmässig gleich gross sind, ist gar nicht so einfach zu begründen, weil das Seil an der Umlenkstelle Impuls mit der Rolle austauscht.
- Die Reibung und weitere Kraftgesetze sind für jedes Teilsystem einzeln zu formulieren.
- Sobald genügend Gleichungen vorhanden sind, kann nach den gesuchten Grössen aufgelöst werden.
- Wendet man dieses Verfahren auf das vorliegende Problem an, erhält man zielgerichtet die korrekte Lösung. Die Antwort auf die Frage, ob man mit solchen Problemstellungen viel über die Grundgesetze der Physik lernt, sei den Didaktikern überlassen.