Flaschenzug

Ein Flaschenzug ist eine einfache Maschine zum Heben von Lasten und verschieben von schweren Körpern. Ein Flaschenzug besteht aus festen und losen Rollen, über die Seile gezogen werden.

Geschichte

Die Kraftminderung durch Anwendung des Hebelgesetzes war schon in der Antike bekannt. Die erste bildliche Darstellung der Kombination von Seil und einfacher Rolle findet sich auf einem assyrischen Relief um 970 v. Chr.. Im alten Rom war der Baukran zur Errichtung der Arenen ein unverzichtbares Gerät. Mit verschiedenen Umlenkrollen versehen, konnten bis zu 7 Tonnen schwere Steinblöcke gehoben werden.

In der Renaissance fand der Flaschenzug seine spektakulärste Anwendung beim Transport und der Aufrichtung des Obelisken auf dem Petersplatz in Rom durch den Ingenieur Domenico Fontana (1586). Bis 1861 blieb der Flaschenzug und seine Anwendung weitgehend unverändert. Erst mit dem Differenzialflaschenzug, der zum ersten Male in London eingesetzt wurde, konnte eine Effizienzsteigerung erreicht werden. Mit diesem Flaschenzug konnte die Kräfteverstärkung bis auf 1:1000 erhöht werden.

Heute werden Flaschenzüge vor allem bei Kränen und Spannvorrichtungen eingesetzt.

Faktorenflaschenzug

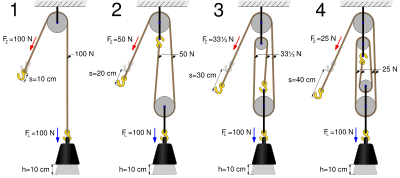
Bei einem Flaschenzug können die Rollen unterschiedlich angeordnet sein. Entscheidend für die "Zugkraft" ist aber immer die Zahl der tragenden Seilabschnitte. Der vom Gravitationsfeld in die Last quellende Impuls fliesst über den Haken an die losen Rollen weg. Dort verzweigt sich der Impulsstrom und teilt sich auf die verschiedenen Seile auf. Die Rollen sorgen dafür, dass alle tragenden Seilabschnitte gleich belastet werden. Wendet man den Knotensatz auf den durch die losen Rollen fliessenden Impulsstrom an, erhält man für die in den tragenden Seilabschnitten fliessenden Ströme die folgende Beziehung

[math]F_{ZS} = \frac {F_L}{n}= \frac{m g}{n}[/math]

n steht für die Anzahl Seile (Tragseile), die zwischen den losen und festen Rollen gespannt sind. In der Berechnungsformel ist stillschweigend vorausgesetzt worden, dass die Rollen keine Reibung aufweisen und dass Seil und Rollen masselos sind. Die oberste Rolle sorgt dafür, dass die Spannung im Zugseil gleich gross wie in den tragenden Seilstücken ist.

Hebt man die Last an, verlängert sich der Teil, der als Zugseil dient, um gleich viel, wie die tragenden Seilabschnitte insgesamt verkürzt worden sind. Folglich gilt für die Geschwindigkeit im Zugseil

[math]v_{ZS} = n v_L[/math]

Lassen sich alle Rollen des Flaschenzuges reibungsfrei drehen und sind sie zudem masselos, fliesst bei einer beliebigen Bewegung die Energie ungehindert durch den Flaschenzug hindurch. Für die zugeordneten Energieströme, die Leistung der Kräfte, gilt dann

[math]I_{W_{ZS}} = P(F_{ZS}) = F_{ZS}v_{ZS} = F_L v_L = P(F_L) = I_{W_L}[/math]

Der Faktorenflaschenzug ist ein Energiewandler (Transformator), der den Energiestrom von einem schwachen auf einen starken Impulsstrom umlädt. Das Übersetzungsverhältnis ist gleich der Zahl der belasteten Seilabschnitte oder doppelt so gross wie die Zahl der losen Rollen an.

Im Flaschenzug fliesst die Energie auf unterschiedlichen Wegen vom Zugseil zur Last. Wählen wir die positive Richtung nach unten, fliesst der Impuls vom Gravitationsfeld in die Last hinein und von dort über die Seile nach oben weg (bei Zugbelastung fliesst der Impuls gegen die Bezugsrichtung, also rückwärts). Die Energie wird über das Zugseil zugeführt und geht dann nach der Umlenkrolle im entsprechenden Seil nach unten weg (weil die Geschwindigkeit dieses Seilabschnitts negativ ist, wird die Energie gegen den Impuls transportiert). In der losen Rolle verzweigt sich der Energiestrom. Ein Teil der Energie wird an die Last abgeführt, der Rest geht über den nächsten Seilabschnitt zusammen mit dem Impuls nach oben weg (dieses Seilstück bewegt sich langsamer nach oben als das gegenüber liegende Stück nach unten). Obwohl die Impulsströme in jedem Seil des Faktorflaschenzugs gleich stark sind, unterscheiden sich die zugeordneten Energieströme. Dies liegt in den unterschiedlichen Geschwindigkeiten der einzelnen Seilabschnitte begründet.

Potenzflaschenzug

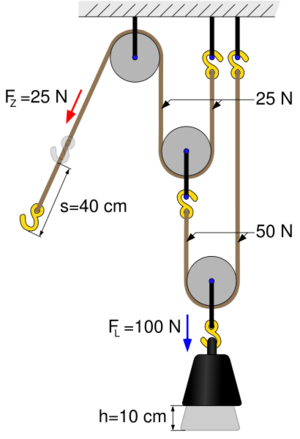
Ein Potenzflaschenzug setzt sich aus einer Serie von losen Rollen zusammen. Der Impuls fliesst von der Last über den Haken in die erste Rolle hinein. Dort wird der Impulsstrom unter die Wirkung des Hebelgesetzes in zwei Teilströme aufgespalten. Der eine Teilstrom geht direkt an die Decke weg, der andere fliesst zu einer zweiten Rolle. Diese Rolle verhält sich wie die erste und teilt den zufliessenden Strom in zwei gleich starke Teilströme auf, wobei der eine Teilstrom wieder an die Decke und der andere an die nächste Rolle abgeleitet wird. Das eine Ende des letzten Seils wird noch einmal umgelenkt und dient als Zugseil.

Jede lose Rolle teilt den von unten kommenden Impulsstrom in zwei gleich grosse Teilströme auf. Folglich halbiert sich die Belastung im beweglichen Teil des Seils von Rolle zu Rolle. Die Kraft auf das Zugseil geht deshalb mit den Potenzen von zwei zürück

[math]F_{ZS} = \frac {F_L}{2^m}[/math]

m steht für die Zahl der losen Rollen.

Weil bei jeder Umlenkrolle das eine Ende des Seils fixiert ist, bewegt sich das andere Ende, das an der nächsten Rolle befestigt ist oder ins Zugseil übergeht doppelt so schnell wie die Rolle. Folglich sind, falls man die Reibung und das Eigengewicht des Flaschenzuges vernachlässigt, die zugeordneten Energieströme im Zugseil und bei der Last gleich stark. Der Potenzflaschenzug ist ein Energiewandler (Transformator), der den Energiestrom von einem schwachen auf einen starken Impulsstrom umlädt. Das Übersetzungsverhältnis steigt mit zwei hoch die Zahl der losen Rollen an.

Differenzialflaschenzug

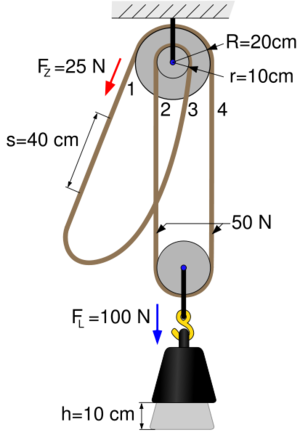
Der Differenzialflaschenzug besteht aus zwei fest miteinander verbundenen Rollen, die verschiedene Radien (R und r) aufweisen und einer losen Rollen. Die Last hängt an der losen Rolle.

Ein wichtiger Vorteil dieses Flaschenzugtyps ist die Material- und Gewichtsersparnis. Die Länge des umlaufenden Seils hängt nur unwesentlich vom Übersetzungsverhältnis ab. Zudem werden nur eine Doppel- und eine lose Rolle benötigt. Weil die beiden Teile der über die Doppelrolle geführten Seilabschnitte unterschiedlich stark belastet werden, muss die Haftreibung zwischen Seil und Rolle stark genug sein. Deshalb wird bei einem Differenzialflaschenzug statt eines Seils oft eine Kette verwendet, die formschlüssig über die an die Kette angepassten Rollen geführt wird.

Der Impuls fliesst beim Differenzialflaschenzug von der Last in die lose Rolle und wird dort unter der Wirkung des Hebelgesetzes in zwei gleich starke Teilströme aufgespalten. Oben, bei der Doppelrolle treffen die beiden Impulsströme auf unterschiedliche Radien, werden also verschieden weit seitlich abgelenkt. Die von den seitwärts fliessenden Impulsströmen erzeugten Drehimpulsquellen sind betragsmässig nicht gleich gross und können sich folglich auch nicht kompensieren. So muss der vom Zugseil zufliessende Impulsstrom eine Drehimpulsquelle erzeugen, welche die Wirkung der beiden andern ausgleicht. Aus dem Kraftbild folgt dann die Gleichgewichtsbedinung bezuglich der Rotation (Summe aller Drehmomente gleich Null)

[math]F_Z R + F_S r = F_S R[/math]

Weil der Impulsstrom in den beiden Tragseilen (F_S) halb so stark wie die Impulsquelle in die Last, die Gewichtskraft F_L, ist, gilt

[math]F_Z = \frac {F_S}{2} \frac {R-r} {R}[/math]

Die Doppelrolle gibt beim Hochziehen der Last über die kleine Rolle Seil frei und wickelt gleichzeitig über die grosse Rolle etwas mehr Seil auf. Die lose Rolle sorgt dafür, dass beide Tragseile gleichmässig verkürzt werden. Dieser Mechanismus bewirkt, dass sich die Geschwindigkeiten wie folgt verhalten

[math]v_L = v_Z \frac {R-r} {2 R}[/math]

Berechnet man den zugeordneten Energiestrom beim Zugseil und bei der Last durch Multiplikation der Kraft (Impulsstromstärke) mit der entsprechenden Geschwindigkeit (zugehöriges Potenzial), erhält man bei einem idealisierten Flaschenzug zweimal den gleichen Wert. Der Differenzialflaschenzug ist ein Energiewandler (Transformator), der den Energiestrom von einem schwachen auf einen starken Impulsstrom umlädt. Das Übersetzungsverhältnis steigt mit einem Faktor, der gleich zweimal das Verhältnis aus grossem Radius und Differenz der beiden Radien ist.

Links