SD-Modell des idealen Gases: Unterschied zwischen den Versionen
User (Diskussion | Beiträge) K (→Modell) |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
In diesem Artikel wird das dynamische Verhalten des idealen Gases modelliert. Dabei zeigt sich, dass die beiden Prozesse mit konstant gehaltener Potentialgrösse (isotherm und isobar) nur näherungsweise als Gleichgewichtsvorgänge nachgebildet werden können. Das hier entwickelte Modell heisst auch [[Carnotor]]. |
|||
==Modell== |
==Modell== |
||
[[Bild: Ideales_Gas.gif|thumb|thermische und mechanische Verbindung des idealen Gases]] |
[[Bild: Ideales_Gas.gif|thumb|thermische und mechanische Verbindung des idealen Gases]] |
||
Der Zustand des [[ideales Gas|idealen Gases]] kann auf zwei Arten verändert werden, durch heizen und kühlen oder durch komprimieren und entspannen. Um diese Prozesse kontrolliert ablaufen zu lassen, gehen wir von folgender Anordnung aus. Das Gas befinde sich in einem Zylinder, der mit einem Kolben verschlossen ist. Der Zylinderboden sei ideal wärmedurchlässig (diatherm), besitze aber selber keine Wärmekapazität. Die Zylinderwände und der Kolben sind absolut wärmeisoliert (adiabatisch). Der reibunsfrei verschiebbare Kolben schliesst das Gas hermetisch gegen eine inkompressible Flüssigkeit ab, welche für den Druckaufbau verantwortlich ist. |
Der Zustand des [[ideales Gas|idealen Gases]] kann auf zwei Arten verändert werden, durch heizen und kühlen oder durch komprimieren und entspannen. Um diese Prozesse kontrolliert ablaufen zu lassen, gehen wir von folgender Anordnung aus. Das Gas befinde sich in einem Zylinder, der mit einem Kolben verschlossen ist. Der Zylinderboden sei ideal wärmedurchlässig (diatherm), besitze aber selber keine Wärmekapazität. Die Zylinderwände und der Kolben sind absolut wärmeisoliert (adiabatisch). Der reibunsfrei verschiebbare Kolben schliesst das Gas hermetisch gegen eine inkompressible Flüssigkeit ab, welche für den Druckaufbau verantwortlich ist. |
||
Das Systeme Gas besitzt eine direkte thermische und eine indirekte hydraulische Verbindung zur Umgebung ( |
Das Systeme Gas besitzt eine direkte thermische und eine indirekte hydraulische Verbindung zur Umgebung ([[Port]] oder Konnektor). Es kann deshalb mit der Umgebung Energie in Form von [[Wärme]] und [[Arbeit]] austauschen. Die beiden Konnektoren können auf drei Arten geschaltet werden |
||
#aktiv: ein Entropie- oder Volumenstrom wird mittels einer Pumpe aufgeprägt. |
#aktiv: ein Entropie- oder Volumenstrom wird mittels einer Pumpe aufgeprägt. |
||
#geschlossen: das Portal lässt keinen Entropie- oder Volumenstrom durch |
#geschlossen: das Portal lässt keinen Entropie- oder Volumenstrom durch |
||
| Zeile 38: | Zeile 40: | ||
==Bilanz== |
==Bilanz== |
||
[[Bild: SD_idealesGas_1.jpg|thumb|Bilanz für Entropie und Volumen]] |
[[Bild: SD_idealesGas_1.jpg|thumb|Bilanz für Entropie und Volumen]] |
||
Das systemdynamische Modell wird wie üblich von der Bilanz der [[Primärgrösse|Primärgrössen]] her aufgebaut. Die zu bilanzierenden Mengen sind die Entropie und das Volumen. Weil hier das Volumen einer inkompressiblen und reibungsfreien Hilfsflüssigkeit bilanziert werden muss, welches den Raum mit dem Gas teilt, ist das Gasvolumen aus der Differen von ''V<sub>tot</sub>'' und ''V<sub>gas</sub>'' zu bestimmen. |
Das systemdynamische [[Modell]] wird wie üblich von der [[Bilanz]] der [[Primärgrösse|Primärgrössen]] her aufgebaut. Die zu bilanzierenden Mengen sind die [[Entropie]] und das Volumen. Weil hier das Volumen einer inkompressiblen und reibungsfreien Hilfsflüssigkeit bilanziert werden muss, welches den Raum mit dem Gas teilt, ist das Gasvolumen aus der Differen von ''V<sub>tot</sub>'' und ''V<sub>gas</sub>'' zu bestimmen. |
||
Der Entropie- und der Volumenstrom können wahlweise aufgeprägt oder unterbrochen sein. Das Gas kann aber auch über ein Element mit grossem Leitwert an die Umgebung ankoppeln |
Der Entropie- und der Volumenstrom können wahlweise aufgeprägt oder unterbrochen sein. Das Gas kann aber auch über ein Element mit grossem Leitwert an die Umgebung ankoppeln |
||
<math>I_S = G_S (T_U - T)</math> |
:<math>I_S = G_S (T_U - T)</math> |
||
<math>I_V = G_V (p_U - p)</math> |
:<math>I_V = G_V (p_U - p)</math> |
||
Koppelt eines der beiden Portale an die Umgebung, ist der Leitwert unter Berücksichtigung der numerischen Stabilität möglichst gross zu wählen. Der Index ''U'' steht für Umgebung. Das Vorzeichen auf beiden Seiten der Gleichungen hängt von der Orientierung der Zuleitung ab. |
Koppelt eines der beiden Portale an die Umgebung, ist der Leitwert unter Berücksichtigung der numerischen Stabilität möglichst gross zu wählen. Der Index ''U'' steht für Umgebung. Das Vorzeichen auf beiden Seiten der Gleichungen hängt von der Orientierung der Zuleitung ab. |
||
| Zeile 52: | Zeile 54: | ||
==konstitutive Gleichungen== |
==konstitutive Gleichungen== |
||
[[Bild: SD_idealesGas_2.jpg|thumb|Berechnung von Druck und Temperatur]] |
[[Bild: SD_idealesGas_2.jpg|thumb|Berechnung von Druck und Temperatur]] |
||
Die konstitutiven Gesetze verknüpfen die Primärmengen mit den zugehörigen [[Potenzial|Potenzialen]]. Die konstitutiven Gesetze für das [[ideales Gas|ideale Gas]] sind das universelle Gasgesetz und die Entropiegleichung. |
Die konstitutiven Gesetze verknüpfen die [[Primärgrösse|Primärmengen]] mit den zugehörigen [[Potenzial|Potenzialen]]. Die konstitutiven Gesetze für das [[ideales Gas|ideale Gas]] sind das universelle Gasgesetz und die Entropiegleichung. |
||
:<math>pV= nRT</math> |
|||
:<math>S = S_0 + n (R ln \frac {V}{V_0} + \hat c_V ln \frac {T}{T_0})</math> |
|||
Weil die Entropiegleichung zwei Mengen, die Entropie und das Volumen, mit nur einem Potenzial, der Temperatur, verknüpft, lösen wir diese nach der Potenzialgrösse auf |
|||
:<math>T = T_0 (\frac {V_0}{V})^{\kappa -1} e^{(S-S_0)/(n \hat c_V)}</math> |
|||
wobei ''κ'' Isentropenexponent oder Adiabatenexponent heisst und gleich <math>\kappa = \frac {\hat c_p}{\hat c_V}</math> ist. |
|||
In einem zweiten Schritt ist aus der Menge ''Volumen'' und dem Potenzial ''Temperatur'' das Potenzial ''Druck'' zu berechnen |
In einem zweiten Schritt ist aus der Menge ''Volumen'' und dem Potenzial ''Temperatur'' das Potenzial ''Druck'' zu berechnen |
||
<math>p = \frac {nRT}{V}</math> |
:<math>p = \frac {nRT}{V}</math> |
||
Mit diesen beiden Schritten (Bilanz und konstitutiven Gesetzen) ist das ideale Gas modelliert. Es ist ein Mythos, zu glauben, dass die Thermodynamik anders als die Mechanik oder die Elektrodynamik nur von der Energie her |
Mit diesen beiden Schritten (Bilanz und konstitutiven Gesetzen) ist das ideale Gas modelliert. Es ist ein Mythos, zu glauben, dass die Thermodynamik anders als die Mechanik oder die Elektrodynamik nur von der Energie her entwickeln werden könne. |
||
==Rolle der Energie== |
==Rolle der Energie== |
||
| Zeile 68: | Zeile 78: | ||
Die Summe aus Wärme und Arbeit ergibt die Änderung der inneren Energie. Aus der inneren Energie, deren Nullpunkt willkürlich gewählt werden kann, lassen sich die [[Enthalpie]] und die [[freie Energie]] berechnen. |
Die Summe aus Wärme und Arbeit ergibt die Änderung der inneren Energie. Aus der inneren Energie, deren Nullpunkt willkürlich gewählt werden kann, lassen sich die [[Enthalpie]] und die [[freie Energie]] berechnen. |
||
[[Kategorie: |
[[Kategorie:Thermo]][[Kategorie:Modelle]] [[Kategorie:ThermoMod]] |
||
Aktuelle Version vom 1. Juli 2007, 07:07 Uhr
In diesem Artikel wird das dynamische Verhalten des idealen Gases modelliert. Dabei zeigt sich, dass die beiden Prozesse mit konstant gehaltener Potentialgrösse (isotherm und isobar) nur näherungsweise als Gleichgewichtsvorgänge nachgebildet werden können. Das hier entwickelte Modell heisst auch Carnotor.
Modell
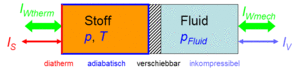
Der Zustand des idealen Gases kann auf zwei Arten verändert werden, durch heizen und kühlen oder durch komprimieren und entspannen. Um diese Prozesse kontrolliert ablaufen zu lassen, gehen wir von folgender Anordnung aus. Das Gas befinde sich in einem Zylinder, der mit einem Kolben verschlossen ist. Der Zylinderboden sei ideal wärmedurchlässig (diatherm), besitze aber selber keine Wärmekapazität. Die Zylinderwände und der Kolben sind absolut wärmeisoliert (adiabatisch). Der reibunsfrei verschiebbare Kolben schliesst das Gas hermetisch gegen eine inkompressible Flüssigkeit ab, welche für den Druckaufbau verantwortlich ist.
Das Systeme Gas besitzt eine direkte thermische und eine indirekte hydraulische Verbindung zur Umgebung (Port oder Konnektor). Es kann deshalb mit der Umgebung Energie in Form von Wärme und Arbeit austauschen. Die beiden Konnektoren können auf drei Arten geschaltet werden
- aktiv: ein Entropie- oder Volumenstrom wird mittels einer Pumpe aufgeprägt.
- geschlossen: das Portal lässt keinen Entropie- oder Volumenstrom durch
- direkt verbunden: das Portal ist über ein Element mit grossem Entropie- oder Volumenleitwert mit der Umgebung verbunden
Mit diesen drei Schaltzuständen können vier Prozesse geführt werden
| Prozess | Beschreibung | thermisches Portal | hydraulisches Portal |
|---|---|---|---|
| isochor | V =konst | aktiv | geschlossen |
| isobar | p =konst | aktiv | direkt verbunden |
| isentrop | S =konst | geschlossen | aktiv |
| isotherm | T =konst | direkt verbunden | aktiv |
Bilanz
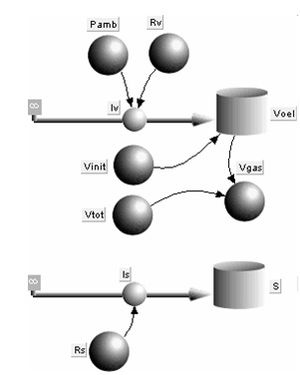
Das systemdynamische Modell wird wie üblich von der Bilanz der Primärgrössen her aufgebaut. Die zu bilanzierenden Mengen sind die Entropie und das Volumen. Weil hier das Volumen einer inkompressiblen und reibungsfreien Hilfsflüssigkeit bilanziert werden muss, welches den Raum mit dem Gas teilt, ist das Gasvolumen aus der Differen von Vtot und Vgas zu bestimmen.
Der Entropie- und der Volumenstrom können wahlweise aufgeprägt oder unterbrochen sein. Das Gas kann aber auch über ein Element mit grossem Leitwert an die Umgebung ankoppeln
- [math]I_S = G_S (T_U - T)[/math]
- [math]I_V = G_V (p_U - p)[/math]
Koppelt eines der beiden Portale an die Umgebung, ist der Leitwert unter Berücksichtigung der numerischen Stabilität möglichst gross zu wählen. Der Index U steht für Umgebung. Das Vorzeichen auf beiden Seiten der Gleichungen hängt von der Orientierung der Zuleitung ab.
Statt eines Leitwertes könnte auch je ein Widerstand definiert werden.
konstitutive Gleichungen
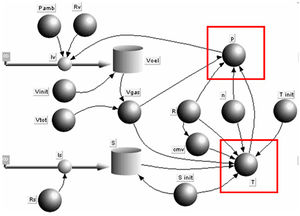
Die konstitutiven Gesetze verknüpfen die Primärmengen mit den zugehörigen Potenzialen. Die konstitutiven Gesetze für das ideale Gas sind das universelle Gasgesetz und die Entropiegleichung.
- [math]pV= nRT[/math]
- [math]S = S_0 + n (R ln \frac {V}{V_0} + \hat c_V ln \frac {T}{T_0})[/math]
Weil die Entropiegleichung zwei Mengen, die Entropie und das Volumen, mit nur einem Potenzial, der Temperatur, verknüpft, lösen wir diese nach der Potenzialgrösse auf
- [math]T = T_0 (\frac {V_0}{V})^{\kappa -1} e^{(S-S_0)/(n \hat c_V)}[/math]
wobei κ Isentropenexponent oder Adiabatenexponent heisst und gleich [math]\kappa = \frac {\hat c_p}{\hat c_V}[/math] ist.
In einem zweiten Schritt ist aus der Menge Volumen und dem Potenzial Temperatur das Potenzial Druck zu berechnen
- [math]p = \frac {nRT}{V}[/math]
Mit diesen beiden Schritten (Bilanz und konstitutiven Gesetzen) ist das ideale Gas modelliert. Es ist ein Mythos, zu glauben, dass die Thermodynamik anders als die Mechanik oder die Elektrodynamik nur von der Energie her entwickeln werden könne.
Rolle der Energie
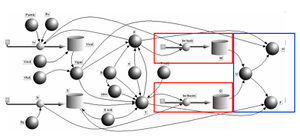
Wärme ist die thermisch und Arbeit die mechanisch ausgetauschte Energie. Mit dem Konzept des zugeordneten Energiestromes können diese beiden Grössen aus dem Entropiestrom und der absoluten Temperatur bzw. aus dem Volumenstrom und dem Druck berechnet werden. Die zugehörigen Integrationen werden mit einer simplen Rohr-Topf-Anordnung programmert.
Die Summe aus Wärme und Arbeit ergibt die Änderung der inneren Energie. Aus der inneren Energie, deren Nullpunkt willkürlich gewählt werden kann, lassen sich die Enthalpie und die freie Energie berechnen.