Lineare passive Zweipole: Unterschied zwischen den Versionen

Aus SystemPhysik
Inhalt hinzugefügt Inhalt gelöscht
 
(4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 2: Zeile 2:
Als einen Zweipol, auch Eintor genannt, bezeichnet man in der Elektrotechnik ein Bauelement oder eine Schaltung mit zwei Klemmen. Das Klemmverhalten wird durch Spannungs-Strom-Verhalten (''U-I''-Relation) beschrieben.
Als einen Zweipol, auch Eintor genannt, bezeichnet man in der Elektrotechnik ein Bauelement oder eine Schaltung mit zwei Klemmen. Das Klemmverhalten wird durch Spannungs-Strom-Verhalten (''U-I''-Relation) beschrieben.


Passive Zweipole beziehen ihre Energie aus dem Stromkreis; sie wirken nicht als [[Energieumlader]]. Unter linear versteht man hier die Proportionalität von Strom und Spannung bzw. ihren Änderungsraten.
Passive Zweipole beziehen ihre Energie aus dem Stromkreis; sie wirken nicht als [[Energiewandler]]. Unter linear versteht man hier die Proportionalität von Strom und Spannung bzw. ihren Änderungsraten.


Man unterteilt die linearen passiven Zweipole in drei Elemente:
Man unterteilt die linearen passiven Zweipole in drei Elemente:
Zeile 26: Zeile 26:
|Kapazität ''C''
|Kapazität ''C''
|Farad F
|Farad F
|<math>\dot U = \frac {1}{C} I</math>
|<math>\dot U=\frac{1}{C}I</math>
|<math>U = \frac {1}{C}\int I dt = \frac {Q_{geflossen}}{C}</math>
|<math>U=\frac{1}{C}\int I dt=\frac {Q_{geflossen}}{C}</math>
|-
|-
|Widerstand ''R''
|Widerstand ''R''
|Ohm &Omega;
|Ohm &Omega;
|<math>U = R I</math>
|<math>U =RI</math>
|
|
|-
|-
|Leitwert ''R''
|Leitwert ''R''
|Siemens S
|Siemens S
|<math>U = \frac {1}{G} I</math>
|<math>U=\frac{1}{G} I</math>
|
|
|-
|-
|Induktivität ''L''
|Induktivität ''L''
|Henri H
|Henri H
|<math>U = L \dot I</math>
|<math>U=L\dot I</math>
|<math>\int U dt = L I</math>
|<math>\int U dt=L I</math>
|}
|}


Zeile 54: Zeile 54:
Die [[Prozessleistung]] über einem elektrischen Zweipol ist gleich Spannung mal Stromstärke
Die [[Prozessleistung]] über einem elektrischen Zweipol ist gleich Spannung mal Stromstärke


<math>P = U I</math>
:<math>P=UI</math>


Setzt man in diese Beziehung die konstutiven Gleichungen für die Systemeigenschaften der drei linearen passiven Zweipole ein erhält man die vom Stromkreis umgesetzte Leistung und nach einer Integration über die Zeit die vom System gespeicherte Energie
Setzt man in diese Beziehung die konstutiven Gleichungen für die Systemeigenschaften der drei linearen passiven Zweipole ein erhält man die vom Stromkreis umgesetzte Leistung und nach einer Integration über die Zeit die vom System gespeicherte Energie
Zeile 65: Zeile 65:
|-
|-
|Kapazität ''C''
|Kapazität ''C''
|<math>P = U I = C U \dot U</math>
|<math>P=UI=CU\dot U</math>
|W = F V<sup>2</sup>/s
|W = F V <sup>2</sup>/s
|<math>W = \frac{1}{2}C U^2 = \frac{Q^2}{2C}</math>
|<math>W=\frac{1}{2}C U^2=\frac{Q^2}{2C}</math>
|-
|-
|Widerstand ''R''
|Widerstand ''R''
|<math>P = U I = R I^2 = \frac {U^2}{R}</math>
|<math>P=UI=RI^2 =\frac{U^2}{R}</math>
|W = &Omega; A<sup>2</sup>
|W = &Omega; A<sup>2</sup>
|
|
|-
|-
|Leitwert ''S''
|Leitwert ''S''
|<math>P = U I = G U^2 = \frac {I^2}{G}</math>
|<math>P=UI=G U^2=\frac{I^2}{G}</math>
|W = S V<sup>2</sup>
|W = S V<sup>2</sup>
|
|
|-
|-
|Induktivität ''L''
|Induktivität ''L''
|<math>P = U I= L I \dot I</math>
|<math>P=UI=LI\dot I</math>
|W = H A<sup>2</sup>
|W = H A<sup>2</sup>
|<math>W = \frac{1}{2}L I^2</math>
|<math>W=\frac{1}{2}LI^2</math>
|}
|}
Kapazität und Induktivität sind Energiespeicher. Im Widerstand wird Energie [[Dissipation|dissipiert]], wird mit Hilfe der vom Strom freigesetzten Energie [[Entropie]] erzeugt.
Kapazität und Induktivität sind Energiespeicher. Im Widerstand wird Energie [[Dissipation|dissipiert]], wird mit Hilfe der vom Strom freigesetzten Energie [[Entropie]] erzeugt.


==Systemdynamische Modelle==
==Systemdynamische Modelle==
[[Bild:LP_System.jpg|thumb|Systemmodelle von ''R'' ''C'' und ''L'']]
Das Verhalten konzentrierter dynamischer Systeme simuliert man durch Integration über die Zeit. Dazu muss das Systemverhalten nach der höchsten zeitlichen Ableitung aufgelöst werden. Da in der [[Physik der dynamischen Systeme]] die Systemeigenschaften nach dem [[Legoprinzip]] formuliert werden, treten nur erste Ableitungen nach der Zeit ([[Änderungsraten]]) auf. Änderungsraten werden als Flüsse (flow) und die Grösse selber als Topf (Stock) dargestellt.
In der [[Elektrodynamik]] tritt die Bilanzgleichung meistens in der reduzierten Form des Knotensatzes auf. Echte Speicher, bezüglich derer man die volle Bilanzgleichung aufstellen kann, sind in der Elektrotechnik kaum anzutreffen. Wie der Widerstand oder die Induktivität gehört auch der Kondensator zu den Stromgliedern (Zweipolen). Denkt man sich die eine Seite des Kondensators geerdet, liefert der andere Teil den Topf (Stock) mit dem Zufluss (flow).


Induktivität und Kapazität wirken auf verschiedenen Ebenen:
*bei der Kapazität muss der Strom zur Ladung aufsummiert (integriert) werden; die Ladung bestimmt dann die Spannung ([[kapazitives Gesetz]])
*bei der Induktivität bewirkt die Spannung eine Änderungsrate der Stromstärke ([[induktives Gesetz]]); diese Änderungsrate muss dann zur Stromstärke aufsummiert (integriert) werden


Im Gegensatz zu den beiden Energiespeichern Kapazität und Induktivität, bei denen eine Änderungsrate oder eine Stromstärke aufsummiert wird, ist die Kausalität beim Widerstand nicht a priori gegeben. Einmal muss eine Spannung in eine Stromstärke und ein andermal eine Stromstärke in einen Widerstand umgerechnet werden.


[[Kategorie: Elektro]]
[[Kategorie: Elektro]]

Aktuelle Version vom 4. September 2007, 19:57 Uhr

Begriff

Als einen Zweipol, auch Eintor genannt, bezeichnet man in der Elektrotechnik ein Bauelement oder eine Schaltung mit zwei Klemmen. Das Klemmverhalten wird durch Spannungs-Strom-Verhalten (U-I-Relation) beschrieben.

Passive Zweipole beziehen ihre Energie aus dem Stromkreis; sie wirken nicht als Energiewandler. Unter linear versteht man hier die Proportionalität von Strom und Spannung bzw. ihren Änderungsraten.

Man unterteilt die linearen passiven Zweipole in drei Elemente:

  • resistiv: Stromstärke und Spannung sind proportional
  • kapazitiv: die Stromstärke ist proportional zur Änderungsrate der Spannung
  • induktiv: die Änderungsrate der Stromstärke ist proportional zur Spannung

Reale Zweipole zeigen alle drei Verhalten, wobei das eine häufig dominiert.

Die Kapazität eines Kondensators, der Widerstand einer leitenden Verbindung und die Induktivität einer Spule hängen vom Material und der Geometrie des Systems ab.

Systemgleichungen

Die Linearität des Zweipolverhaltens ermöglicht die Beschreibung des Systemverhaltens mit einer einzigen Konstanten:

  • Widerstand R mit der Einheit Ohm (Ω) für ein rein resistives Glied
  • Kapazität C mit der Einheit Fahrad (F) für eine rein kapazitives Glied
  • Induktivität L mit der Einheit Henri (H) für eine rein induktives Glied
Zweipol Einheit momentan integral
Kapazität C Farad F [math]\dot U=\frac{1}{C}I[/math] [math]U=\frac{1}{C}\int I dt=\frac {Q_{geflossen}}{C}[/math]
Widerstand R Ohm Ω [math]U =RI[/math]
Leitwert R Siemens S [math]U=\frac{1}{G} I[/math]
Induktivität L Henri H [math]U=L\dot I[/math] [math]\int U dt=L I[/math]
  • Beim Widerstand folgt der Strom direkt der Spannung.
  • Bei der Kapazität ändert der Strom die Spannung; die Spannung ist proportional zum Integralwert der Stromstärke über die Zeit; die "Spannung läuft dem Strom hinterher".
  • Bei der Induktivität ändert die Spannung die Stromstärke. Die Stromstärke ist proportional zum Integralwert der Spannung über die Zeit; der "Strom läuft der Spannung hinterher".

Leitwert und Widerstand sind reziprok zueinander. Bei Serieschaltung werden die Widerstände direkt zum Ersatzwiderstand und Leitwerte reziprok zum reziproken Ersatzleitwert addiert. Bei Parallelschaltung müssen die Leitwerte direkt und die Widerstände reziprok addiert werden. Kapazitäten verhalten sich bei Serie- und Parallelschaltung wie Leitwerte, Induktivitäten wie Widerstände.

Energiebetrachtung

Die Prozessleistung über einem elektrischen Zweipol ist gleich Spannung mal Stromstärke

[math]P=UI[/math]

Setzt man in diese Beziehung die konstutiven Gleichungen für die Systemeigenschaften der drei linearen passiven Zweipole ein erhält man die vom Stromkreis umgesetzte Leistung und nach einer Integration über die Zeit die vom System gespeicherte Energie

Zweipol Leistung Einheit Energie
Kapazität C [math]P=UI=CU\dot U[/math] W = F V 2/s [math]W=\frac{1}{2}C U^2=\frac{Q^2}{2C}[/math]
Widerstand R [math]P=UI=RI^2 =\frac{U^2}{R}[/math] W = Ω A2
Leitwert S [math]P=UI=G U^2=\frac{I^2}{G}[/math] W = S V2
Induktivität L [math]P=UI=LI\dot I[/math] W = H A2 [math]W=\frac{1}{2}LI^2[/math]

Kapazität und Induktivität sind Energiespeicher. Im Widerstand wird Energie dissipiert, wird mit Hilfe der vom Strom freigesetzten Energie Entropie erzeugt.

Systemdynamische Modelle

Systemmodelle von R C und L

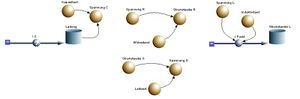
In der Elektrodynamik tritt die Bilanzgleichung meistens in der reduzierten Form des Knotensatzes auf. Echte Speicher, bezüglich derer man die volle Bilanzgleichung aufstellen kann, sind in der Elektrotechnik kaum anzutreffen. Wie der Widerstand oder die Induktivität gehört auch der Kondensator zu den Stromgliedern (Zweipolen). Denkt man sich die eine Seite des Kondensators geerdet, liefert der andere Teil den Topf (Stock) mit dem Zufluss (flow).

Induktivität und Kapazität wirken auf verschiedenen Ebenen:

  • bei der Kapazität muss der Strom zur Ladung aufsummiert (integriert) werden; die Ladung bestimmt dann die Spannung (kapazitives Gesetz)
  • bei der Induktivität bewirkt die Spannung eine Änderungsrate der Stromstärke (induktives Gesetz); diese Änderungsrate muss dann zur Stromstärke aufsummiert (integriert) werden

Im Gegensatz zu den beiden Energiespeichern Kapazität und Induktivität, bei denen eine Änderungsrate oder eine Stromstärke aufsummiert wird, ist die Kausalität beim Widerstand nicht a priori gegeben. Einmal muss eine Spannung in eine Stromstärke und ein andermal eine Stromstärke in einen Widerstand umgerechnet werden.

Abgerufen von „http://systemdesign.ch/index.php?title=Lineare_passive_Zweipole&oldid=5392“