Viskosität

Die Viskosität ist ein Mass für die Zähflüssigkeit eines Fluids (Flüssigkeit oder Gas). Je grösser die Viskosität desto dickflüssiger, d.h. weniger fliessfähig ist das Fluid. Die Viskosität bestimmt das Widerstandsverhalten eines Systems gegenüber dem durchfliessenden Impulsstrom. Gelegentlich wird Zähigkeit als Synonym für Viskosität verwendet. Der Kehrwert der Viskosität ist die Fluidität, ein Mass für die Fliessfähigkeit eines Fluids.

Der Begriff Viskosität geht auf den typisch zähflüssigen Saft der Beeren der Misteln (Viscum) zurück. Viskosität bedeutet also wörtlich "Misteligkeit".

Definition

Gedankenexperiment zur Viskosität

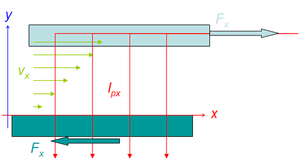
Man stelle sich zwei im Abstand x angeordnete Platten der Fläche A vor. Zwischen diesen Platten befindet sich eine Flüssigkeit, die an beiden Platten haftet (benetzende Flüssigkeit). Wird nun Platte 2 mit der Geschwindigkeit v bewegt, so nimmt sie die Flüssigkeitsschicht in unmittelbarer Nachbarschaft mit. Da Platte 1 ruht, bewegt sich auch die angrenzende Flüssigkeit nicht. Der durchfliessende x-Impulsstrom ist umso stärker, je schneller sich die Platten bewegen. Im Bereich der Flüssigkeit strömt der x-Impuls in y-Richtung also quer zu seiner eigenen Bezugsrichtung (die x-Impulsstromstärke bezüglicher einer Platte nennt man Kraft F_x).

Nimmt nun die Geschwindigkeit in der Flüssigkeit linear mit y zu und wächst der in diesem Bereich querfliessende x-Impulsstrom linear mit der Geschwindigkeitsdifferenz zwischen den Platten an, spricht man von einer Newtonschen Flüssigkeit. Die Stärke des durch die Flüssigkeit durchtretenden Impulsstromes nimmt proportional mit dem Querschnitt und der Geschwindigkeitsdifferenz zu sowie reziprok zum Abstand der beiden Platten ab

[math]I_{px} = \eta \frac {\Delta v_x}{\Delta y} A[/math]

Die Proportionalitätskonstante η wird als dynamische Viskosität oder einfach nur Viskosität bezeichnet. Die dynamische Viskosität hat die Einheit Pas. Ein Stoff hat eine Viskosität von 1 Ns/m², wenn pro Quadratmeter Plattenfläche und einem Plattenabstand von 1 m auf jede der beiden Platten eine Kraft von 1 N einwirken muss, damit sich die Platten mit einer Geschwindigkeit von 1 m/s gegeneinander verschieben. Oft wird die dynamische Viskosität mit der Dichte dividiert. Diese Grösse nennt man dann kinematische Viskosität. Die kinematische Viskosität wird in m²/s angegeben.

lokale Beschreibung

Um die Materialeigenschaft Viskosität lokal zu beschreiben, formt man die definierende Gleichung um

[math]j_{pxy} = -\eta \frac {\partial v_x}{\partial y} [/math]

Die Impulsstromdichte ist bei einer Newtonschen Flüssigkeiten proportional zum Geschwindigkeitsgradienten.

Eine Reibung beschreibt man lokal als Zusammenhang zwischen der Stromdichte einer mengenartigen Grösse und dem entsprechenden Gradienten des Potenzials. Folglich muss eine mechanische Reibung im Innern eines Körpers als Zusammenhang zwischen der Impulsstromdichte und dem Geschwindigkeitsgradienten formuliert werden. Die Impulsstromdichte (negativer Spannungstensor) und der symmetrische Teil des Geschwindigkeitsgradienten lassen sich je in einen Gestaltänderungs- und einen Volumenänderungsteil zerlegen. Isotrope Materialien beschreibt man dann mit je einer skalaren Funktion zwischen diesen beiden speziellen Tensoren. Im Falle der Newtonschen Reibung reduzieren sich diese beiden Funktionen auf die Schwerviskosität η und Volumenviskosität ζ

[math]j_{pij}^g = -\eta w_{ij}^g[/math] und [math]j_{pij}^i = -\zeta w_{ij}^i[/math]

Messmethoden

Die Viskosität wird mittels einer laminaren Strömung gemessen. Entweder lässt man eine bestimmte Menge Flüssigkeit durch ein System hindurchfliessen oder die Flüssigkeit umströmt einen Körper. Im ersten Fall wird die Viskosität hydrodynamisch, aus dem Zusammenhang zwischen Volumenstromstärke und Druck, ermittelt, im zweiten Fall misst man direkt oder indirekt den Impulsstrom oder den Drehimpulsstrom. Folgende Geräte dienen der Viskositätsmessung:

• Kapillarviskosimeter
• Kugelfallviskosimeter
• Rotationsviskosimeter