Kugel vom Eiffelturm: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) K (→Energie) |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Eine Kugel fällt aus einer Höhe von 300 Meter (Höhe des Eiffelturms) hinunter. Wie lange dauert diese Bewegung und mit welcher Geschwindigkeit trifft die Kugel auf dem Boden auf? |
Eine Kugel fällt aus einer Höhe von 300 Meter (Höhe des Eiffelturms) hinunter. Wie lange dauert diese Bewegung und mit welcher Geschwindigkeit trifft die Kugel auf dem Boden auf? Unter [[Fall mit Luftwiderstand]] wird die zugehörige Differentialgleichung integriert. |
||
==Vakuum== |
==Vakuum== |
||
Version vom 3. Februar 2009, 12:34 Uhr
Eine Kugel fällt aus einer Höhe von 300 Meter (Höhe des Eiffelturms) hinunter. Wie lange dauert diese Bewegung und mit welcher Geschwindigkeit trifft die Kugel auf dem Boden auf? Unter Fall mit Luftwiderstand wird die zugehörige Differentialgleichung integriert.
Vakuum
Würde man die Kugel im Vakuum fallen lassen, wäre die Beschleunigung betragsmässig gleich der Gravitationsfeldstärke. Die Geschwindigkeit der Kugel würde jede Sekunde um 9.81 m/s zunehmen. Ihre Endgeschwindigkeit wäre dann gleich
- [math]v_e=\sqrt{2gh}[/math] = 76.7 m/s
Dies ergibt eine Fallzeit von
- [math]t=\frac{v_e}{g}[/math] = 7.8 s
Endgeschwindigkeit
Das Gravitationsfeld führt der Kugel mit konstanter Rate Impuls zu. Die Zufuhrrate, Gewichtskraft genannt, ist gleich Masse mal Gravitationsfeldstärke
- [math]F_G=mg=\varrho V g=\varrho \frac{4\pi}{3}r^3g[/math]
Der Luftwiderstand führt mit zunehmender Geschwindigkeit immer mehr Impuls ab
- [math]F_W=\frac{\varrho_L}{2}v^2c_WA[/math]
Im Gleichgewichtszustand entzieht die Luft der Kugel gleich viel Impuls wie das Gravitationsfeld zuführt. Folglich gilt
- [math]\varrho \frac{4\pi}{3}r^3g=\frac{\varrho_L}{2}v_e^2c_W\pi r^2[/math]
Löst man diese Gleichgewichtsbedingung nach der Geschwindigkeit auf, folgt
- [math]v_e=\sqrt{\frac{8}{3 c_W}\frac{\varrho}{\varrho_L}rg}[/math]
Die Endgeschwindigkeit nimmt bei einer Vollkugel mit der Wurzel aus dem Radius und der Dichte zu. Für eine Holzkugel mit einer Dichte von 600 kg/m3 und einem Durchmesser von 10 cm liefert die Gleichgewichtsbedingung eine Endgeschwindigkeit von 40.4 m/s oder 146 km/h.
Modell
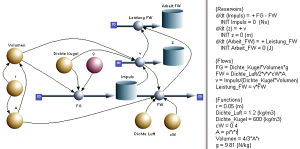
Die Impulsbilanz bildet das Rückgrat dieses Modells zur eindimensionalen Translationsmechanik. Das Gravitationsfeld führt der Kugel mit der konstanten Rate FG = m*g Impuls zu. Die Luft entzieht der Kugel mit zunehmender Geschwindigkeit immer mehr Impuls. Der statische Auftrieb, der auch in Luft wirkt, ist hier nicht berücksichtigt bzw. mit der Dichte der Kugel verrechnet worden.
Die Geschwindigkeit eines Körper ist dynamisch durch den Quotienten aus Impuls und Masse festgelegt. Weil die Geschwindigkeit kinematisch als Änderungsrate des Ortes definiert ist, kann die Strecke mittels einer "Rohr-Topf-Anordnung" berechnet werden. In diesem Fall muss das Rohr (flow) in den Topf (Reservoir) hinein orientiert sein. Weil die Gravitationskraft als positiv angenommen worden ist, nimmt auch die Strecke mit der Zeit zu.
Die Dichte der Luft und die Stärke des Gravitationsfeldes ändern sich wenig auf 300 m Höhe. Als Ausbauvariante könnte man den Widerstandsbeiwert in Funktion der Geschwindigkeit angeben.
Simulation
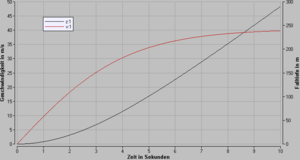
Setzt man die folgenden Werte
- Radius der Kugel 0.05 m
- Dichte der Kugel (Holz) 600 kg/m3
- Dichte der Luft 1.2 kg/m3
ins Modell ein, erreicht die Kugel nach 10 s eine Falltiefe von etwa 300 m. Ihre Geschwindigkeit erreicht dann mit etwa 40 m/s beinahe den erwarteten Endwert.
Mit Hilfe einer Parameterstudie (Parameter:Batch Runs oder Ctrl+M) kann der Radius oder die Dichte der Kugel stufenweise verändert werden. Nach der unmittelbar ausgeführten Simulation werden die zugehörigen Graphen bündelweise angezeigt.
Energie
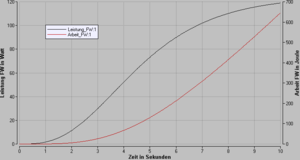
In der Mechanik hat die Geschwindigkeit drei Funktionen:
- dynamisch:Quotient aus Impuls und Masse
- kinematisch: Änderungsrate des Orts
- energetisch: Energiebeladungsmass des Impulsstromes
Gemäss ihrer dritten Funktion ordnet die Geschwindigkeit jedem Impulsstrom einen Energiestrom zu. Bezieht man die Stärke des Impulsstromes auf einen Körper, verknüpft die Geschwindigkeit die Kraft mit der Leistung dieser Kraft
- [math]P(\vec F)=\vec v\cdot\vec F=v_xF_x+v_yF_y+v_zF_z[/math]
Die Leistung des Luftwiderstandes ist demnach gleich dem Luftwiderstand mal die Geschwindigkeit der Kugel. Wird diese Leistung mit einer "Rohr-Topf-Anordnung" aufsummiert, erhält man die total dissipierte Energie.
Auf einer zweiten Ebene hätte man ein vollständiges Energiemodell aufbauen können. Dazu bildet man die Impulsbilanz nochmals ab und multipliziert zusätzlich alle Impulsströme (Kräfte) mit der Geschwindigkeit des Körpers. Weil die Energiebilanz hier wenig Neues bringt, ist darauf verzichtet worden.