Freie Energie: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
==Motivation== |
==Motivation== |
||
Gas unter hohem Druck hat ein grosses Arbeitsvermögen, das spontan in einer Explosion oder kontrolliert in einem [[Pressluftmotor]] freigesetzt werden kann. Strömt das Gas schnell aus, kühlt sich |
[[Bild:Freie-Energie.jpg|thumb|Arbeit gleich Änderung der freien Energie]]Gas unter hohem Druck hat ein grosses Arbeitsvermögen, das spontan in einer Explosion oder kontrolliert in einem [[Pressluftmotor]] freigesetzt werden kann. Strömt das Gas schnell aus, kühlt sich der verbleibende Teil ab. Fliesst das Gas dagegen langsam aus dem Behälter, sinkt die Temperatur kaum ab, weil [[Wärme]] aus der Umgebung zuströmt. Nun hängt die vom Gas gespeicherte Energie, die [[innere Energie]] des Gases, nur unwesentlich vom Druck ab. Beim [[ideales Gas|idealen Gas]] nimmt die innere Energie sogar nur mit der Temperatur und überhaupt nicht mit dem Druck zu. Das Bild zeigt den [[Carnotor]], dessen thermischer [[Port]] mit einem Wärmebad kurz geschlossen ist. Sucht man nun nach einer Grösse, die aus den Zuständen des im Carnotor enthaltenen Stoffes berechnet werden kann und gleich der Änderung der mechanischen Energie (auch Arbeit genannt) ist, stösst man auf die freie Energie. |
||
Um den scheinbaren Widerspruch zwischen mit dem Druck zunehmendem Arbeitsvermögen und druckunabhägniger innerer Energie zu klären, kann die [[Energiebilanz]] bezüglich eines Gases |
Um den scheinbaren Widerspruch zwischen mit dem Druck zunehmendem Arbeitsvermögen und druckunabhägniger innerer Energie zu klären, kann die [[Energiebilanz]] bezüglich eines Gases |
||
:<math>I_{W_{therm}} |
:<math>I_{W_{therm}}+I_{W_{mech}}=\dot W</math> |
||
umgeformt werden. Unter Berücksichtigung der Homogenität (überall gleicher Zustand) und der daraus abzuleitenden Reversibilität der Prozessführung kann der thermische [[zugeordneter Energiestrom|Energiestrom]] auf die |
umgeformt werden. Unter Berücksichtigung der Homogenität (überall gleicher Zustand) und der daraus abzuleitenden Reversibilität der Prozessführung kann der thermische [[zugeordneter Energiestrom|Energiestrom]] auf die [[Zustandsgrösse]]n [[Temperatur]] und [[Entropie]] umgeformt werden |
||
:<math>I_{W_{mech}} |
:<math>I_{W_{mech}}=\dot W-I_{W_{therm}}=\dot W-T I_S=\dot W-T\dot S</math> |
||
Solange die Umgebung die Temperatur auf einem festen Wert hält, darf die rechte Seite der Gleichung als Speicher für die mechanische Energie aufgefasst werden. Diese Argumentation, bei der die Änderung der inneren Energie und die mit der Umwelt unkontrolliert ausgetauschte [[Wärme]] einem gemeinsamen Speicher zugewiesen werden, folgt der Begriffsbildung der [[potenzielle Energie|potenziellen Energie]], bei der die gespeicherte Energie fälschlicherweise dem Körper und nicht dem [[elektromagnetisches Feld|elektromagnetischen Feld]] oder dem [[Gravitationsfeld]] zugewiesen wird. Die Argumentation mit der mechanisch gespeicherten Energie bleibt konsistent, solange das Gas bei konstanter Temperatur expandiert oder komprimiert wird. Sobald das Gas aber unterschiedliche Prozesse durchläuft, muss man die Idee einer mechanisch gespeicherten Energie, eines im Stoff enthaltenen Arbeitsvermögens, fallen lassen. |
|||
| ⚫ | Die [[Enthalpie]], die für die thermisch gespeicherte Energie steht, übernimmt eine zur freien Energie äquivalente Funktion. Nur steht dort die Wärme statt der Arbeit im Zentrum des Interesses. Die '''Enthalpie''' ist ein Mass für die thermisch gespeicherte Energie, solange die Umwelt den '''Druck''' stabilisiert. Die '''freie Energie''' ist ein Mass für die mechanisch gespeicherte Energie, solange die Umwelt die '''Temperatur konstant''' hält. |
||
==Definition== |
==Definition== |
||
Die freie Energie, die der Fiktion des mechanischen Energiespeichers entspringt, hat als sauber definierte Zustandsgrösse einen Platz in der Thermodynamik gefunden. Für homogene Gase ist die freie Energie gleich der [[innere Energie|inneren Energie]] minus das Produkt aus [[Entropie]] und [[Temperatur]] |
Die freie Energie, die der Fiktion des mechanischen Energiespeichers entspringt, hat als sauber definierte [[Zustandsgrösse]] einen Platz in der Thermodynamik gefunden. Für homogene Gase ist die freie Energie gleich der [[innere Energie|inneren Energie]] minus das Produkt aus [[Entropie]] und [[Temperatur]] |
||
:<math>F |
:<math>F=W-TS</math> oder in alter Schreibweise <math>F=U-TS</math> |
||
Die innere Energie oder Selbstenergie eines Systems, die gemäss der Relativtitätstheorie gleich Mass mal Lichtgeschwindigkeit im Quadrat ist, wird üblicherweise bei einem bestimmten Zustand (''T<sub>0</sub>'', ''p<sub>0</sub>'') gleich Null gesetzt. |
|||
Komprimiert oder expandiert man ein homogenes Gas bei konstant gehalterner Temperatur, gilt |
Komprimiert oder expandiert man ein homogenes Gas bei konstant gehalterner Temperatur, gilt |
||
:<math>I_{W_{mech}} |
:<math>I_{W_{mech}}=\dot W-T\dot S=\dot F</math> |
||
| ⚫ | Bei konstant gehaltener Temperatur ist der mechanische Energiestrom, die mechanische Leistung, gleich der Änderungsrate der freien Energie. Die [[Enthalpie]], die für die thermisch gespeicherte Energie steht, übernimmt eine zur freien Energie äquivalente Funktion. Nur steht dort die Wärme statt der Arbeit im Zentrum des Interesses. Die '''Enthalpie''' ist ein Mass für die thermisch gespeicherte Energie, solange die Umwelt den '''Druck''' stabilisiert. Die '''freie Energie''' ist ein Mass für die mechanisch gespeicherte Energie, solange die Umwelt die '''Temperatur konstant''' hält. |
||
==isotherme Expansion== |
|||
Lässt man ein [[ideales Gas]] isotherm expandieren, bleibt die [[innere Energie]], die nur von der Temperatur abhängt, konstant. Die durch die Expansion in Form von Arbeit abgegebene Energie wird vollständig von der Umgebung in Form von Wärme zugeführt. Die Energiebilanz für die isotherme Expansion eines idealen Gases lässt demnach die vom Gas gespeicherte Energie unverändert |
|||
:<math>I_{W_{mech}} + I_{W_{therm}} = \dot W = 0</math> |
|||
Formt man die Energiebilanz über die [[zugeordneter Energiestrom|Zuordnung]] auf die Zustandsgrössen um, was bei reversibler Prozessführung erlaubt ist, gewinnt man einen Zusammenhang zwischen den Änderungsraten der Entropie und des Volumens (im Carnotor verdrängt das zufliessende Fluid das Gas; deshalb ist die Änderungsrate des Gasvolumens gleich minus die Stärke des Volumenstromes) |
|||
:<math>I_{W_{mech}} + I_{W_{therm}} = p I_{V_{Fluid}} + T I_S = -p \dot V + T \dot S</math> |
|||
Lässt man nun ein Gas bei konstanter Temperatur um das ''x''-fache des Anfangsvolumens expandieren, beträgt die Expansionsarbeit |
|||
:<math>W_{ex} = -\int p dV = -\int \frac {n R T}{V} dV = -n R T \ln(x)</math> |
|||
Aufgrund der aus der Energiebilanz gewonnen Beziehung zwischen Entropie und Volumen ist dann die zugeführt Entropie gleich |
|||
:<math>S = -\frac {W_{ex}}{T} = n R \ln(x)</math> |
|||
Somit hat die freie Energie bei dieser Expansion um |
|||
:<math>\Delta F = \Delta W - T S = 0 - n R T \ln(x)</math> |
|||
abgenommen, was gerade der Expansionsarbeit entspricht. Die freie Energie ist eine Art Arbeitsvermögen eines auf konstanter Temperatur gehaltenen Gases. Das Arbeitsgas wirkt bei der isothermen Expansion als Wandler, der Wärme vollständig in Arbeit umformt. Die bei diesem Vorgang aufgenommene Entropie vermindert aber die weitere Wandlungsfähigkeit, was durch die Verminderung der freien Energie ausgedrückt wird. |
|||
Bei konstant gehaltener Temperatur ist der mechanische Energiestrom, die mechanische Leistung, gleich der Änderungsrate der freien Energie. |
|||
[[Kategorie:Thermo]] |
[[Kategorie:Thermo]] |
||
Aktuelle Version vom 29. März 2009, 16:20 Uhr
Die freie Energie (auch Helmholtz-Energie) ist ein Mass für das Arbeitsvermögen eines thermodynamischen Systems. Die freie Energie wird in Joule (J) gemessen. Als Formelzeichen wird oft F verwendet.
Motivation
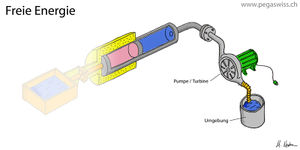
Gas unter hohem Druck hat ein grosses Arbeitsvermögen, das spontan in einer Explosion oder kontrolliert in einem Pressluftmotor freigesetzt werden kann. Strömt das Gas schnell aus, kühlt sich der verbleibende Teil ab. Fliesst das Gas dagegen langsam aus dem Behälter, sinkt die Temperatur kaum ab, weil Wärme aus der Umgebung zuströmt. Nun hängt die vom Gas gespeicherte Energie, die innere Energie des Gases, nur unwesentlich vom Druck ab. Beim idealen Gas nimmt die innere Energie sogar nur mit der Temperatur und überhaupt nicht mit dem Druck zu. Das Bild zeigt den Carnotor, dessen thermischer Port mit einem Wärmebad kurz geschlossen ist. Sucht man nun nach einer Grösse, die aus den Zuständen des im Carnotor enthaltenen Stoffes berechnet werden kann und gleich der Änderung der mechanischen Energie (auch Arbeit genannt) ist, stösst man auf die freie Energie.
Um den scheinbaren Widerspruch zwischen mit dem Druck zunehmendem Arbeitsvermögen und druckunabhägniger innerer Energie zu klären, kann die Energiebilanz bezüglich eines Gases
- [math]I_{W_{therm}}+I_{W_{mech}}=\dot W[/math]
umgeformt werden. Unter Berücksichtigung der Homogenität (überall gleicher Zustand) und der daraus abzuleitenden Reversibilität der Prozessführung kann der thermische Energiestrom auf die Zustandsgrössen Temperatur und Entropie umgeformt werden
- [math]I_{W_{mech}}=\dot W-I_{W_{therm}}=\dot W-T I_S=\dot W-T\dot S[/math]
Solange die Umgebung die Temperatur auf einem festen Wert hält, darf die rechte Seite der Gleichung als Speicher für die mechanische Energie aufgefasst werden. Diese Argumentation, bei der die Änderung der inneren Energie und die mit der Umwelt unkontrolliert ausgetauschte Wärme einem gemeinsamen Speicher zugewiesen werden, folgt der Begriffsbildung der potenziellen Energie, bei der die gespeicherte Energie fälschlicherweise dem Körper und nicht dem elektromagnetischen Feld oder dem Gravitationsfeld zugewiesen wird. Die Argumentation mit der mechanisch gespeicherten Energie bleibt konsistent, solange das Gas bei konstanter Temperatur expandiert oder komprimiert wird. Sobald das Gas aber unterschiedliche Prozesse durchläuft, muss man die Idee einer mechanisch gespeicherten Energie, eines im Stoff enthaltenen Arbeitsvermögens, fallen lassen.
Definition
Die freie Energie, die der Fiktion des mechanischen Energiespeichers entspringt, hat als sauber definierte Zustandsgrösse einen Platz in der Thermodynamik gefunden. Für homogene Gase ist die freie Energie gleich der inneren Energie minus das Produkt aus Entropie und Temperatur
- [math]F=W-TS[/math] oder in alter Schreibweise [math]F=U-TS[/math]
Die innere Energie oder Selbstenergie eines Systems, die gemäss der Relativtitätstheorie gleich Mass mal Lichtgeschwindigkeit im Quadrat ist, wird üblicherweise bei einem bestimmten Zustand (T0, p0) gleich Null gesetzt.
Komprimiert oder expandiert man ein homogenes Gas bei konstant gehalterner Temperatur, gilt
- [math]I_{W_{mech}}=\dot W-T\dot S=\dot F[/math]
Bei konstant gehaltener Temperatur ist der mechanische Energiestrom, die mechanische Leistung, gleich der Änderungsrate der freien Energie. Die Enthalpie, die für die thermisch gespeicherte Energie steht, übernimmt eine zur freien Energie äquivalente Funktion. Nur steht dort die Wärme statt der Arbeit im Zentrum des Interesses. Die Enthalpie ist ein Mass für die thermisch gespeicherte Energie, solange die Umwelt den Druck stabilisiert. Die freie Energie ist ein Mass für die mechanisch gespeicherte Energie, solange die Umwelt die Temperatur konstant hält.
isotherme Expansion
Lässt man ein ideales Gas isotherm expandieren, bleibt die innere Energie, die nur von der Temperatur abhängt, konstant. Die durch die Expansion in Form von Arbeit abgegebene Energie wird vollständig von der Umgebung in Form von Wärme zugeführt. Die Energiebilanz für die isotherme Expansion eines idealen Gases lässt demnach die vom Gas gespeicherte Energie unverändert
- [math]I_{W_{mech}} + I_{W_{therm}} = \dot W = 0[/math]
Formt man die Energiebilanz über die Zuordnung auf die Zustandsgrössen um, was bei reversibler Prozessführung erlaubt ist, gewinnt man einen Zusammenhang zwischen den Änderungsraten der Entropie und des Volumens (im Carnotor verdrängt das zufliessende Fluid das Gas; deshalb ist die Änderungsrate des Gasvolumens gleich minus die Stärke des Volumenstromes)
- [math]I_{W_{mech}} + I_{W_{therm}} = p I_{V_{Fluid}} + T I_S = -p \dot V + T \dot S[/math]
Lässt man nun ein Gas bei konstanter Temperatur um das x-fache des Anfangsvolumens expandieren, beträgt die Expansionsarbeit
- [math]W_{ex} = -\int p dV = -\int \frac {n R T}{V} dV = -n R T \ln(x)[/math]
Aufgrund der aus der Energiebilanz gewonnen Beziehung zwischen Entropie und Volumen ist dann die zugeführt Entropie gleich
- [math]S = -\frac {W_{ex}}{T} = n R \ln(x)[/math]
Somit hat die freie Energie bei dieser Expansion um
- [math]\Delta F = \Delta W - T S = 0 - n R T \ln(x)[/math]
abgenommen, was gerade der Expansionsarbeit entspricht. Die freie Energie ist eine Art Arbeitsvermögen eines auf konstanter Temperatur gehaltenen Gases. Das Arbeitsgas wirkt bei der isothermen Expansion als Wandler, der Wärme vollständig in Arbeit umformt. Die bei diesem Vorgang aufgenommene Entropie vermindert aber die weitere Wandlungsfähigkeit, was durch die Verminderung der freien Energie ausgedrückt wird.