Lösung zu Rosenkrieg: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 10. Februar 2010, 18:41 Uhr

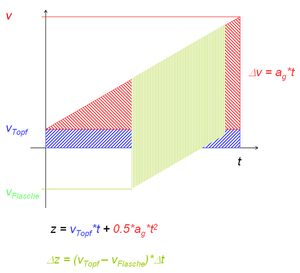
Vernachlässigt man die Wirkung der umgebenden Luft, ist die Beschleunigung aller fallender Körper gleich der Gravitationsfeldstärke. Aus diesem Grund nennt man die Stärke des Gravitationsfeldes an der Erdoberfläche oft Erdbeschleunigung. Weil alle geworfene Körper im Vakuum gleich stark beschleunigt sind, erscheinen ihre Vertikalbewegungen im v-t-Diagramm als Geraden mit einer Steigung von 10 m/s².

Die Skizze zeigt das Geschwindigkeits-Zeit-Diagramm des Topfs und der Weinflasche. Alle Fragen zur Kinematik können mit Hilfe dieses Diagramms berechnet werden.

Die Falltiefe entspricht der Fläche unter dem v-t-Diagramm. Diese Fläche setzt sich aus einem Rechteck (Anfangsgeschwindigkeit mal Zeit), blau im Diagramm, und einem Dreieck (rot) (Geschwindigkeitszunahme mal Zeit durch zwei) zusammen [math]z=v_0 t+\frac{1}{2}\Delta v t=v_0 t+\frac{1}{2}a_g t^2[/math]. Beide Flächen zusammen sollen z = 7 m ergeben. Die Lösung dieser quadratischen Gleichung für t liefert eine Fallzeit von einer Sekunde.
In einer Sekunde wächst die Geschwindigkeit des Topf um 10 m/s an. Folglich würde der Topf mit 2 m/s + 10 m/s = 12 m/s (43.2 km/h) auf dem Kopf aufschlagen, siehe auch v-t-Diagramm.
Der Topf würde dann 0.8 kg * 12 m/s = 9.6 Ns Impuls speichern. Nimmt man einen Bremsweg von 6 cm an, würde der Topf diesen Impuls in 0.06 m / (12 m/s / 2) = 0.01 s (Weg / mittlere Geschwindigkeit) abgeben, was eine mittlere Impulsstromstärke (Kraft) von 9.6 Ns / 0.01 s = 960 N ergibt.
In den ersten 0.4 Sekunden ( = 1 s - 0.6 s), d. h. bis zum Abwurf der Weinflasche, erreicht der Topf eine Geschwindigkeit von 2 m/s + 10 m/s * 0.4 s = 6 m/s. Dabei fällt er um 0.4 s * (2 m/s + 6 m/s) / 2 = 1.6 m hinunter. Danach bewegen sich Weinflasche und Topf mit einer konstanten Relativgeschwindigkeit von 6 m/s - (-4 m/s) = 10 m/s. Somit benötigen sie für den restlichen Abstand von 7 m - 1.6 m = 5.4 m noch 5.4 m / 10 m/s = 0.54 s. Zu diesem Zeitpunkt (0.4 s + 0.54 s = 0.94 s, das ist weniger als 1 s) hat der Topf den Kopf noch nicht erreicht, aber die Weinflasche fällt schon wieder nach unten.

Aufgabe

@@ Zeile 5: / Zeile 5: @@
 #In einer Sekunde wächst die Geschwindigkeit des Topf um 10 m/s an. Folglich würde der Topf mit 2 m/s + 10 m/s = 12 m/s (43.2 km/h) auf dem Kopf aufschlagen, siehe auch v-t-Diagramm.
 #Der Topf würde dann 0.8 kg * 12 m/s = 9.6 Ns [[Impuls]] speichern. Nimmt man einen Bremsweg von 6 cm an, würde der Topf diesen Impuls in 0.06 m / (12 m/s / 2) = 0.01 s (Weg / mittlere Geschwindigkeit) abgeben, was eine mittlere Impulsstromstärke (Kraft) von 9.6 Ns / 0.01 s = 960 N ergibt.
-#In den ersten 0.4 Sekunden fällt der Topf um 1.6 m hinunter. Danach bewegen sich Weinflasche und Topf mit einer konstante Relativgeschwindigkeit von 10 m/s. Somit benötigen sie für die restlichen 5.4 m noch 0.54 s. Zu diesem Zeitpunkt fällt auch die Weinflasche schon wieder nach unten.
+#In den ersten 0.4 Sekunden ( = 1 s - 0.6 s), d. h. bis zum Abwurf der Weinflasche, erreicht der Topf eine Geschwindigkeit von 2 m/s + 10 m/s * 0.4 s = 6 m/s. Dabei fällt er um 0.4 s * (2 m/s + 6 m/s) / 2 =  1.6 m hinunter. Danach bewegen sich Weinflasche und Topf mit einer konstanten Relativgeschwindigkeit von 6 m/s - (-4 m/s) = 10 m/s. Somit benötigen sie für den restlichen Abstand von 7 m - 1.6 m = 5.4 m noch 5.4 m / 10 m/s = 0.54 s. Zu diesem Zeitpunkt (0.4 s + 0.54 s = 0.94 s, das ist weniger als 1 s) hat der Topf den Kopf noch nicht erreicht, aber die Weinflasche fällt schon wieder nach unten.
 '''[[Rosenkrieg|Aufgabe]]'''