Lösung zu Aviatik 2012/2: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
|||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Lösung 1== |
==Lösung 1== |
||
#Änderung von Enthalpie und Entropie im System: <math>W_{th}=\Delta H=mc\Delta T</math> = 419 kJ; <math>\Delta S=mc\ln\left(\frac{T_2}{T_1}\right)</math> = 1.40 kJ/K |
|||
#zu pumpende Entropie <math>S_{WP}=\frac{W_{th}}{T_{oben}}</math> = 1.30 kJ/K; Pumparbeit <math>W=\Delta T_{WP}S_{WP}</math> = 51.9 kJ |
|||
#zwischen Wärmepumpe und Wasser produzierte Entropie: <math>S_{prod}=\Delta S-S_{WP}</math> = 98 J/K |
|||
#aufzuwendende Energie ist gleich Energiezunahme im Wasser minus Energie aus der Umgebung: <math>S_{Umg}=\Delta S</math>; <math>W_{Umg}=S\cdot T_{Umg}</math>; <math>W_{rev}=\Delta H-W_{Umg}</math> = 24.2 kJ |
|||
::<videoflash>_yoCV9W1UZg|649|360</videoflash> |
::<videoflash>_yoCV9W1UZg|649|360</videoflash> |
||
==Lösung 2== |
==Lösung 2== |
||
#[[Diesel-Zyklus]] |
|||
#<math>p_2=p_1\left(\frac{V_1}{V_2}\right)^\kappa</math> = 66.3 bar; <math>T_2=T_1\left(\frac{V_1}{V_2}\right)^{\kappa-1}</math> = 994 K; |
|||
#<math>T_3=T_2+\Delta T=T_2+\frac{\Delta H}{n\hat c_p}</math> = 994 K + 857 K = 1851 K |
|||
#isobar Volumen 3 berechnen <math>V_3=V_2\frac{T_3}{T_2}</math> = 0.0466 Liter; isentrop Temperatur vier berechnen <math>T_4=T_3\left(\frac{V_3}{V_4}\right)^{\kappa-1}</math> = 717 K;isentrope Expansion: <math>\Delta W=W_{mech}=n\hat c_V\Delta T_{23}</math> = -437 J; |
|||
::<videoflash>Ru4QogH7-4k|649|360</videoflash> |
::<videoflash>Ru4QogH7-4k|649|360</videoflash> |
||
==Lösung 3== |
==Lösung 3== |
||
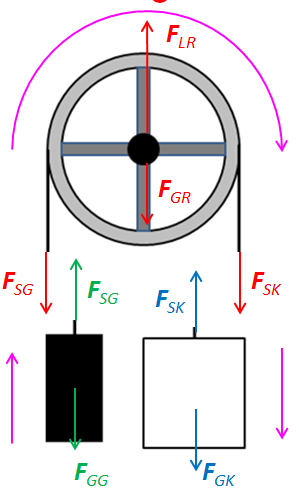
:::[[Datei:Aviatik 12 2 3L.PNG|Schnittbilder]] |
|||
::Gegengewicht: <math>F_{SG}-F_{GG}=m_Ga_G</math> |
|||
::Kabine: <math>F_{GK}-F_{SK}=m_Ka_K</math> |
|||
::Antriebsrad: <math>F_{SK}r-F_{SG}r=J\alpha</math> |
|||
::Kinematik: <math>a_G=a_K=r\alpha</math> |
|||
:::<math>a=g\frac{m_K-m_G}{m_G+m_K+\frac{J}{r^2}}</math> = 1.51 m/s<sup>2</sup> |
|||
:::<math>F_{SG}=m_G(a+g)</math> = 2.26 kN |
|||
::<videoflash>vBSPiEOwWO8|649|360</videoflash> |
::<videoflash>vBSPiEOwWO8|649|360</videoflash> |
||
| Zeile 16: | Zeile 36: | ||
==Lösung 5== |
==Lösung 5== |
||
Zur Beantwortung der letzten drei Fragen sollte man unbedingt ein [[Flüssigkeitsbild]] zeichnen. |
|||
#Im mitrotierenden System misst man ein [[Zentrifugalfeld]] der Stärke <math>g_z=\omega^2r=\frac{4\pi^2}{T^2}r</math>. Nach der Umlaufzeit auflösen <math>T=2\pi\sqrt{\frac{r}{g_z}}</math> = 24.2 s |
|||
#<math>W_A=L_1\frac{\omega_1-\omega_2}{2}</math> = 222MJ |
|||
#<math>M=\frac{L_1/2}{t}</math> = 2.24 10<sup>4</sup> Nm |
|||
#Aus dem [[Flüssigkeitsbild]] ist zu entnehmen, dass die Hälfte des gesamten [[Drehimpuls]]es um drei Viertel der maximalen Differenz der Winkelgeschwindigkeiten angehoben werden muss <math>\Delta W_A=\frac{L_1}{2}\frac{3(\omega_1-\omega_2)}{4}</math> =166 MJ |
|||
::Die Leistung beträgt deshalb <math>P=\frac{\Delta W_A}{\Delta t}</math> = 3.85 kW |
|||
::Drehoment zu Beginn <math>M_a=\frac{2P}{\omega_1-\omega_2}</math> = 11.2 kNm |
|||
::Drehoment am Schluss <math>M_a=\frac{P}{\omega_1-\omega_2}</math> = 5.6 kNm |
|||
::<videoflash>fSxWwfzmMwc|649|360</videoflash> |
::<videoflash>fSxWwfzmMwc|649|360</videoflash> |
||
Aktuelle Version vom 25. Juni 2014, 11:46 Uhr
Lösung 1
- Änderung von Enthalpie und Entropie im System: [math]W_{th}=\Delta H=mc\Delta T[/math] = 419 kJ; [math]\Delta S=mc\ln\left(\frac{T_2}{T_1}\right)[/math] = 1.40 kJ/K
- zu pumpende Entropie [math]S_{WP}=\frac{W_{th}}{T_{oben}}[/math] = 1.30 kJ/K; Pumparbeit [math]W=\Delta T_{WP}S_{WP}[/math] = 51.9 kJ
- zwischen Wärmepumpe und Wasser produzierte Entropie: [math]S_{prod}=\Delta S-S_{WP}[/math] = 98 J/K
- aufzuwendende Energie ist gleich Energiezunahme im Wasser minus Energie aus der Umgebung: [math]S_{Umg}=\Delta S[/math]; [math]W_{Umg}=S\cdot T_{Umg}[/math]; [math]W_{rev}=\Delta H-W_{Umg}[/math] = 24.2 kJ
- <videoflash>_yoCV9W1UZg|649|360</videoflash>
Lösung 2
- Diesel-Zyklus
- [math]p_2=p_1\left(\frac{V_1}{V_2}\right)^\kappa[/math] = 66.3 bar; [math]T_2=T_1\left(\frac{V_1}{V_2}\right)^{\kappa-1}[/math] = 994 K;
- [math]T_3=T_2+\Delta T=T_2+\frac{\Delta H}{n\hat c_p}[/math] = 994 K + 857 K = 1851 K
- isobar Volumen 3 berechnen [math]V_3=V_2\frac{T_3}{T_2}[/math] = 0.0466 Liter; isentrop Temperatur vier berechnen [math]T_4=T_3\left(\frac{V_3}{V_4}\right)^{\kappa-1}[/math] = 717 K;isentrope Expansion: [math]\Delta W=W_{mech}=n\hat c_V\Delta T_{23}[/math] = -437 J;
- <videoflash>Ru4QogH7-4k|649|360</videoflash>
Lösung 3
- Kabine: [math]F_{GK}-F_{SK}=m_Ka_K[/math]
- Antriebsrad: [math]F_{SK}r-F_{SG}r=J\alpha[/math]
- Kinematik: [math]a_G=a_K=r\alpha[/math]
- [math]a=g\frac{m_K-m_G}{m_G+m_K+\frac{J}{r^2}}[/math] = 1.51 m/s2
- [math]F_{SG}=m_G(a+g)[/math] = 2.26 kN
- <videoflash>vBSPiEOwWO8|649|360</videoflash>
Lösung 4
- <videoflash>WivYnwH52mk|649|360</videoflash>
Lösung 5
Zur Beantwortung der letzten drei Fragen sollte man unbedingt ein Flüssigkeitsbild zeichnen.
- Im mitrotierenden System misst man ein Zentrifugalfeld der Stärke [math]g_z=\omega^2r=\frac{4\pi^2}{T^2}r[/math]. Nach der Umlaufzeit auflösen [math]T=2\pi\sqrt{\frac{r}{g_z}}[/math] = 24.2 s
- [math]W_A=L_1\frac{\omega_1-\omega_2}{2}[/math] = 222MJ
- [math]M=\frac{L_1/2}{t}[/math] = 2.24 104 Nm
- Aus dem Flüssigkeitsbild ist zu entnehmen, dass die Hälfte des gesamten Drehimpulses um drei Viertel der maximalen Differenz der Winkelgeschwindigkeiten angehoben werden muss [math]\Delta W_A=\frac{L_1}{2}\frac{3(\omega_1-\omega_2)}{4}[/math] =166 MJ
- Die Leistung beträgt deshalb [math]P=\frac{\Delta W_A}{\Delta t}[/math] = 3.85 kW
- Drehoment zu Beginn [math]M_a=\frac{2P}{\omega_1-\omega_2}[/math] = 11.2 kNm
- Drehoment am Schluss [math]M_a=\frac{P}{\omega_1-\omega_2}[/math] = 5.6 kNm
- <videoflash>fSxWwfzmMwc|649|360</videoflash>