U-Rohr: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==System== |
==System== |
||
Drückt man die eine Flüssigkeitssäule eines beidseitig offenen U-Rohr-[[Manometer]]s durch Anlegen eines Überdrucks hinunter, schwingt die Flüssigkeit danach um die Gleichgewichtslage, bis sich das System wieder beruhigt hat. Ob man dabei ein mit Wasser oder mit Quecksilber gefülltes Manometer nimmt, spielt bezüglich des dynamischen Verhaltens kaum eine Rolle. Man stellt weder bezüglich Schwingungsdauer noch bezüglich Abklingverhalten einen grossen Unterschied zwischen den beiden Flüssigkeiten fest. Beim Quecksilber muss man aber einen etwa dreizehn Mal stärkeren Überdruck erzeugen als bei Wasser, um die gleich Auslenkung zu erhalten. |
|||
Die Dauer oder Periode der Schwingung kann mittels einer allgemeinen Überlegung bestimmt werden. Vom elektrischen Schwingkreis weiss man, dass die Periode proportional zum geometrischen Mittel aus Kapazität und Induktivität ist |
|||
:<math>T=2\pi\sqrt{LC}</math> |
|||
Nun ist die hydraulische Induktivität eines mit Wasser gefüllten Rohrs gleich |
|||
:<math>L_V=\varrho\frac{l}{A}</math> |
|||
Die beiden vertikalen Teile des U-Rors bilden je eine Kapazität, die in Serie geschaltet sind. Folglich ist die Gesamtkapazität beider Säulen gleich der Hälfte der Einzelkapazität |
|||
:<math>C_V=\frac{A}{2\varrho g}</math> |
|||
Setzt man beide Systemeigenschaften in die Formel für die Periode ein, folgt |
|||
:<math>T=2\pi\sqrt{\frac{l}{2g}}</math> |
|||
Die Periode hängt nur von der Länge der Flüssigkeitssäule und von der [[Erdbeschleunigung|Gravitationsfeldstärke]] ab. Die Dichte der Flüssigkeit und der Querschnitt spielen keine Rolle. |
|||
==Modell== |
==Modell== |
||
| Zeile 6: | Zeile 24: | ||
Das System U-Rohr kann in zwei Kapazitäten, einen Widerstand und eine Induktivität zerlegt werden. Die hydraulische Kapazität eines zylindrischen Gefässes ist gleich Querschnitt durch Dichte und Gravitationsfeldstärke. Widerstand und Induktivität können vom [[gerades Rohrstück|geraden Rohr]] übernommen werden. Messungen zeigen, dass diese Modellierung des Widerstandes zu grosse Abweichungen zwischen Modell- und Systemverhalten führt. |
Das System U-Rohr kann in zwei Kapazitäten, einen Widerstand und eine Induktivität zerlegt werden. Die hydraulische Kapazität eines zylindrischen Gefässes ist gleich Querschnitt durch Dichte und Gravitationsfeldstärke. Widerstand und Induktivität können vom [[gerades Rohrstück|geraden Rohr]] übernommen werden. Messungen zeigen, dass diese Modellierung des Widerstandes zu grosse Abweichungen zwischen Modell- und Systemverhalten führt. |
||
Das Volumen der beiden Kapazitäten darf |
Das Volumen der beiden Kapazitäten (vertikale Rohrstücke) darf auf den Gleichgewichtszustand bezogen werden. Damit bleibt das Gesamtvolumen der beiden Kapazitäten während des ganzen Vorganges gleich Null. Der zugehörige Druck, der auf den Spiegel der ruhenden Flüssigkeit bezogen wird, schwingt deshalb auch um den Nullpunkt herum. Im vorliegenden Modell ist der Widerstand als reine Laminarströmung modelliert worden. Diese Annahme ist bequem und numerisch stabil, dürfte aber das Verhalten des realen Systems nicht allzu präzis beschreiben. Der Widerstandes in einem gekrümmten Rohr mit pulsierender Strömung ist ein komplexes Phänomen, das sicher nicht einfach zu beschreiben ist. |
||
Das [[Systemdiagramm]] zeigt die dynamische Struktur mit der [[Volumenbilanz]], den beiden |
Das [[Systemdiagramm]] zeigt die dynamische Struktur mit der [[Volumenbilanz]], den beiden Rückkopplungen über [[kapazitives Gesetz|kapazitives]], [[resistives Gesetz|resistives]] und [[induktives Gesetz]] sowie der Energiebetrachtung (zweite Bilanzebene). Die Energiebilanz umfasst die Änderung in den beiden Kapazitäten ([[Gravitationsfeld|Gravitationsenergie]]), den Energieumsatz im Rohr ([[Bewegungsenergie]] sowie die [[Dissipation|dissipierte]] Energie). |
||
==Simulation== |
==Simulation== |
||
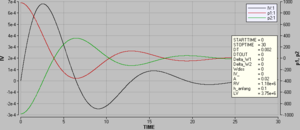
[[Bild:URohr_D1.png|thumb|IV, Δp<sub>links</sub> sowie Δp<sub>rechts</sub>]] |
|||
Das erste Diagramm zeigt den Druckverlauf in den beiden vertikalen Rohrstücken sowie den zugehörigen Volumenstrom. Der zeitliche Verlauf des Drucks entspricht dem der Füllhöhe. Verglichen mit dem Experiment klingt die Schwingung zu schnell ab. Um das Abklingverhalten der Schwingung besser zu modellieren, müsste man das Reibungsmodell verfeinern und die zugehörigen Parameter mittels ein paar Messungen schätzen. |
|||
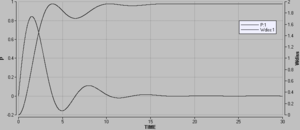
[[Bild:URohr_D2.png|thumb|IV, Δp<sub>links</sub> sowie Δp<sub>rechts</sub>]] |
|||
Das zweite Diagramm zeigt die hydraulische [[Prozessleistung]] der Wassersäule sowie die vom Wasser insgesamt aufgenommene Energie. Die Bezeichnung ''Diss'' für [[Dissipation]] ist hier nicht ganz korrekt. Um die dissipierte Energie zu rechnen, dürfte man bei der Prozessleistung nur die Druckdifferenz über dem Widerstandselement einsetzen. Die hier formulierte Prozessleistung bezieht sich aber auf das resistive und das induktive Glied. |
|||
Aktuelle Version vom 8. Oktober 2008, 05:50 Uhr
System
Drückt man die eine Flüssigkeitssäule eines beidseitig offenen U-Rohr-Manometers durch Anlegen eines Überdrucks hinunter, schwingt die Flüssigkeit danach um die Gleichgewichtslage, bis sich das System wieder beruhigt hat. Ob man dabei ein mit Wasser oder mit Quecksilber gefülltes Manometer nimmt, spielt bezüglich des dynamischen Verhaltens kaum eine Rolle. Man stellt weder bezüglich Schwingungsdauer noch bezüglich Abklingverhalten einen grossen Unterschied zwischen den beiden Flüssigkeiten fest. Beim Quecksilber muss man aber einen etwa dreizehn Mal stärkeren Überdruck erzeugen als bei Wasser, um die gleich Auslenkung zu erhalten.
Die Dauer oder Periode der Schwingung kann mittels einer allgemeinen Überlegung bestimmt werden. Vom elektrischen Schwingkreis weiss man, dass die Periode proportional zum geometrischen Mittel aus Kapazität und Induktivität ist
- [math]T=2\pi\sqrt{LC}[/math]
Nun ist die hydraulische Induktivität eines mit Wasser gefüllten Rohrs gleich
- [math]L_V=\varrho\frac{l}{A}[/math]
Die beiden vertikalen Teile des U-Rors bilden je eine Kapazität, die in Serie geschaltet sind. Folglich ist die Gesamtkapazität beider Säulen gleich der Hälfte der Einzelkapazität
- [math]C_V=\frac{A}{2\varrho g}[/math]
Setzt man beide Systemeigenschaften in die Formel für die Periode ein, folgt
- [math]T=2\pi\sqrt{\frac{l}{2g}}[/math]
Die Periode hängt nur von der Länge der Flüssigkeitssäule und von der Gravitationsfeldstärke ab. Die Dichte der Flüssigkeit und der Querschnitt spielen keine Rolle.
Modell
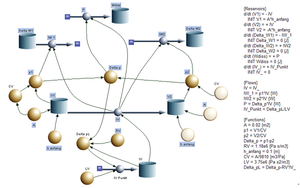
Das System U-Rohr kann in zwei Kapazitäten, einen Widerstand und eine Induktivität zerlegt werden. Die hydraulische Kapazität eines zylindrischen Gefässes ist gleich Querschnitt durch Dichte und Gravitationsfeldstärke. Widerstand und Induktivität können vom geraden Rohr übernommen werden. Messungen zeigen, dass diese Modellierung des Widerstandes zu grosse Abweichungen zwischen Modell- und Systemverhalten führt.
Das Volumen der beiden Kapazitäten (vertikale Rohrstücke) darf auf den Gleichgewichtszustand bezogen werden. Damit bleibt das Gesamtvolumen der beiden Kapazitäten während des ganzen Vorganges gleich Null. Der zugehörige Druck, der auf den Spiegel der ruhenden Flüssigkeit bezogen wird, schwingt deshalb auch um den Nullpunkt herum. Im vorliegenden Modell ist der Widerstand als reine Laminarströmung modelliert worden. Diese Annahme ist bequem und numerisch stabil, dürfte aber das Verhalten des realen Systems nicht allzu präzis beschreiben. Der Widerstandes in einem gekrümmten Rohr mit pulsierender Strömung ist ein komplexes Phänomen, das sicher nicht einfach zu beschreiben ist.
Das Systemdiagramm zeigt die dynamische Struktur mit der Volumenbilanz, den beiden Rückkopplungen über kapazitives, resistives und induktives Gesetz sowie der Energiebetrachtung (zweite Bilanzebene). Die Energiebilanz umfasst die Änderung in den beiden Kapazitäten (Gravitationsenergie), den Energieumsatz im Rohr (Bewegungsenergie sowie die dissipierte Energie).
Simulation
Das erste Diagramm zeigt den Druckverlauf in den beiden vertikalen Rohrstücken sowie den zugehörigen Volumenstrom. Der zeitliche Verlauf des Drucks entspricht dem der Füllhöhe. Verglichen mit dem Experiment klingt die Schwingung zu schnell ab. Um das Abklingverhalten der Schwingung besser zu modellieren, müsste man das Reibungsmodell verfeinern und die zugehörigen Parameter mittels ein paar Messungen schätzen.
Das zweite Diagramm zeigt die hydraulische Prozessleistung der Wassersäule sowie die vom Wasser insgesamt aufgenommene Energie. Die Bezeichnung Diss für Dissipation ist hier nicht ganz korrekt. Um die dissipierte Energie zu rechnen, dürfte man bei der Prozessleistung nur die Druckdifferenz über dem Widerstandselement einsetzen. Die hier formulierte Prozessleistung bezieht sich aber auf das resistive und das induktive Glied.