Lösung zu Aviatik 2007/3: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
##Die Stärke des Volumenstromes ist gleich Querschnitt mal mittlere Strömungsgeschwindigkeit, was hier 13.7 l/s ergibt. |
##Die Stärke des Volumenstromes ist gleich Querschnitt mal mittlere Strömungsgeschwindigkeit, was hier 13.7 l/s ergibt. |
||
##Dem ausfliessenden Wasser kann der folgende Energiestrom zugeordnete werden <math> I_W=\left(p+\varrho g h+\frac \varrho 2 v^2\right)I_V</math>. Um die dissipierte Leistung zu berechnen, bildet man die Differenz zwischen der kinetischen Energiedichte im reibungsfreien und im reibungsbehafteten Fall und mulitpliziert diesen Wert mit dem effektiv auftretenden Volumenstrom <math>P=\left(\frac \varrho 2 v_{ideal}^2-\frac \varrho 2 v_{real}^2\right)I_V</math> = 337 W. |
##Dem ausfliessenden Wasser kann der folgende Energiestrom zugeordnete werden <math> I_W=\left(p+\varrho g h+\frac \varrho 2 v^2\right)I_V</math>. Um die dissipierte Leistung zu berechnen, bildet man die Differenz zwischen der kinetischen Energiedichte im reibungsfreien und im reibungsbehafteten Fall und mulitpliziert diesen Wert mit dem effektiv auftretenden Volumenstrom <math>P=\left(\frac \varrho 2 v_{ideal}^2-\frac \varrho 2 v_{real}^2\right)I_V</math> = 337 W. |
||
#Die Schubkraft ist gleich <math> F_S=(v_2-v_1)I_m</math> und die vom Triebwerk auf den Luftstrom zu übertragende Leistung <math> P=\frac 12\left(v_2^2-v_1^2\right)I_m=\frac{v_1+v_1}{2}F_S</math>. |
|||
##<math>v_2=v_1+\frac{F_S}{I_m}</math> = 250 m/s + 80 m/s = 330 m/s |
|||
##<math> P=\frac{v_1+v_1}{2}F_S</math> = 19.72 MW |
|||
##<math> F_S=(v_{2K}-v_1)\frac {I_m}{5}+(v_{2M}-v_1)\frac {4I_m}{5}</math>. Daraus folgt <math> v_{2K}=\frac{5F_S}{4I_m}+\frac{5v_1}{4}-\frac{v_{2K}}{4}</math> = 312.5 m/s |
|||
##<math>P =\frac 12\left(v_{2K}^2-v_1^2\right)\frac{I_m}{5}+\frac 12\left(v_{2M}^2-v_1^2\right)\frac{4I_m}{5}</math> = 8.288 MW + 11.95 MW = 20.24 MW. |
|||
#Eine Wärmepumpe fördert [[Entropie]]. Dazu benötigt sie elektrische Energie. |
|||
##Der thermisch abgegebene Energiestrom ist 5 mal stärker als die totale Prozessleistung. Folglich beträgt die Prozessleistung 2 kW und der vom Kältebad her zufliessende Energiestrom hat eine Stärke von 8 kW. |
|||
##Der vom Kältebad zufliessende Entropiestrom hat eine Stärke von <math>I_{S1}=\frac{I_{W1}}{T_1}</math> = 27.3 W/K. Der an den Heizwasservorlauf abfliessende Entropiestrom ist gleich <math>I_{S2}=\frac{I_{W2}}{T_2}</math> = 31.95 W/K. Die Differenz zwischen diesen beiden Stromstärken von 4.6 W/K entspricht der Produktionsrate. |
|||
##Eine ideale Wärmepumpe benötigt eine Prozessleistung von <math> P=(T_2-T_1)I_S</math> = 639 W. Die Differenz von 1361 W zur effektiven Leistung von 2 kW ist die Verlustleistung. |
|||
##Bei verlustfreiem, reversiblem Betrieb gilt <math> COP=\frac{I_{W2}}{P}=\frac{T_2I_S}{(T_2-T_1)I_S}=\frac{T_2}{T_2-T_1}</math> = 15.65. |
|||
#Die von einem Körper beim isobaren Heizen oder Kühlen aufgenommene bzw. abgegebene Wärme ist gleich der Änderung der [[Enthalpie]]. |
|||
##<math>\Delta H=m\left(c_W(T_s-T_1)-q+c_E(T_2-T_s)\right)</math> = -91.96 MJ und <math>\Delta S=m\left(c_W\ln\frac{T_s}{T_1}-\frac{q}{T_s}+c_E\ln\frac{T_2}{T_s}\right)</math> = -335.9 kJ/K |
|||
##Die von der Wärmepumpe aufzunehmende Entropie ist gleich der vom Wasser abzugebenden Energie dividiert durch die Eingangstemperatur <math> S_{Pumpe}=\frac{\Delta H}{T_{unten}}</math> = 378.4 kJ/K. Die aufzuwendende Pumparbeit ist dann gleich <math> W=(T_{oben}-T_{unten})S_{Pumpe}</math> = 22.7 MJ |
|||
##Die an die Umwelt übertragene Wärme ist gleich ''W<sub>th</sub>'' = 91.96 MJ + 22.7 MJ = 114.66 MJ. Diese Energie wird zusammen mit <math> S_{Umwelt}=\frac{W_{th}}{T_{Umwelt}}</math> = 391.3 kJ/K der Umwelt zugeführt. Ein Vergleich mit der von der Wärmepumpe geförderten Entropie zeigt, dass 13 kJ/K produziert worden ist. |
|||
##Die Umwelt gibt weniger Entropie ab, als das Wasser aufnimmt. Der Unterschied muss produziert werden <math> S_{prod}=\Delta S-\frac{\Delta H}{T_{Umwelt}}</math> = 335.9 kJ/K - 313.8 kJ/K = 22 kJ/K |
|||
#Mischt man heisses und kaltes Wasser, bleibt die Energie (Enthalpie) im Idealfall erhalten. Die Gesamtentropie nimmt aber in jedem Fall zu, weil bei jedem irreversiblen Vorgang Entropie erzeugt wird. |
|||
##Das heisse Wasser wird von 80°C auf 40°C abgekühlt und das kalte von 15°C auf 40°C erwärmt. Folglich beträgt der Anteil heisses Wasser 5/13 und der Anteil Kaltwasser 8/13. Die 400 Liter Boilerwasser sind demnach mit 400/5*8 = 640 Liter Kaltwasser zu mischen. |
|||
##Die dabei produzierte Entropie ist gleich <math>\Delta S=m_1 c\ln{\frac{T_m}{T_1}}+m_2 c\ln{\frac{T_m}{T_2}}</math> = 21.66 kJ/K |
|||
##Änderungen im Heisswasser: <math>\Delta H=mc(T_m-T_1)</math> = - 67.04 MJ und <math>\Delta S=mc\ln{\frac{T_m}{T_1}}</math> = -201.6 kJ/K; Energieabgabe an die Umwelt <math>W_{th}=-\Delta S T_{Umwelt}</math> = 58.06 MJ; nutzbare Energie ''W<sub>nutz</sub>'' = 67.04 MJ - 58.06 MJ = 8.98 MJ. |
|||
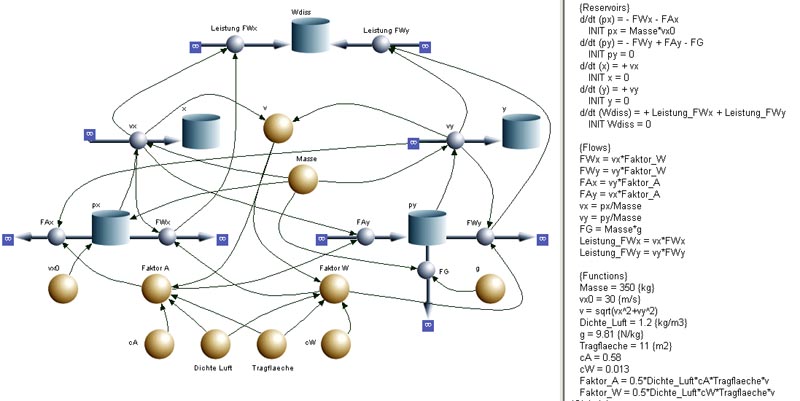
#Auf das Segelflugzeug wirken das Gravitationsfeld und die Luft ein. Die Wirkung der Luft kann in eine Widerstandskraft (parallel zu Anströmung) und eine Auftriebskraft (normal zur Anströmung) zerlegt werden. Im Gleichgewichtszustand ist die Luftkraft (Summe aus Widerstand und Auftrieb) gleich der Gewichtskraft. Hier wird angenommen, dass die Beiwerte konstant sind und ein Verhältnis von 45:1 bilden. Das Flugzeug habe eine Masse von 350 kg und eine Tragfläche von 11 m<sup>2</sup>. Nimmt man an, dass die grösste Gleitzahl von 45 bei einer Geschwindigkeit von 108 km/h erreicht wird, ergibt sich ein Auftriebsbeiwert (Auftriebszahl, Auftriebskoeffizient) von 0.58. Der Widerstandsbeiwert ist dann gleich 0.013. Das Bild zeigt das Systemdiagramm (flowchart) und die Gleichungen. |
|||
[[Bild:Segelflugzeug1 SD.jpg]] |
|||
'''[[Aviatik 2007/3|Aufgabe]]''' |
|||
Aktuelle Version vom 22. April 2008, 11:06 Uhr
- Der konvektive Energietransport erfolgt in vier Teilen. Drei dieser vier Terme sind mechanisch begründet. Der vierte Term beschreibt die innere Energie des Fluids [math] I_W=\left(p+\varrho g h+\frac \varrho 2 v^2+\varrho_W\right)I_V=\left(\frac p \varrho+gh+\frac {v^2}{2}+w\right)I_m[/math]. In der hier gestellten Aufgabe sind nur die drei mechanischen Terme zu berücksichtigen.
- Die Ausflussgeschwindigkeit ergibt sich aus der "Umwandlung" von potentieller in kinetische Energie. Dies beschreibt das Ausflussgesetz von Torricelli mit fünf Meter "Fallhöhe" [math]v=\sqrt{2gh}[/math] = 9.9 m/s.
- Zur Beantwortung dieser Frage formuliert man das Gesetz von Bernoulli für den tiefsten und den fraglichen Punkt [math]p_1+\varrho gh_1+\frac \varrho 2 v_1=p_2+\varrho gh_2+\frac \varrho 2 v_2[/math]. Nun sind die beiden Geschwindigkeiten gleich gross und die Höhe in Punkt 1 darf gleich Null gesetzt werden. Weil der Über- oder Unterdruck gefragt ist, muss der Druck in Punkt 1 auf Null gesetzt werden. Daraus folgt [math]p_{2e}=-\varrho g h_2[/math] = -0.196 bar.
- Die Stärke des Volumenstromes ist gleich Querschnitt mal mittlere Strömungsgeschwindigkeit, was hier 13.7 l/s ergibt.
- Dem ausfliessenden Wasser kann der folgende Energiestrom zugeordnete werden [math] I_W=\left(p+\varrho g h+\frac \varrho 2 v^2\right)I_V[/math]. Um die dissipierte Leistung zu berechnen, bildet man die Differenz zwischen der kinetischen Energiedichte im reibungsfreien und im reibungsbehafteten Fall und mulitpliziert diesen Wert mit dem effektiv auftretenden Volumenstrom [math]P=\left(\frac \varrho 2 v_{ideal}^2-\frac \varrho 2 v_{real}^2\right)I_V[/math] = 337 W.
- Die Schubkraft ist gleich [math] F_S=(v_2-v_1)I_m[/math] und die vom Triebwerk auf den Luftstrom zu übertragende Leistung [math] P=\frac 12\left(v_2^2-v_1^2\right)I_m=\frac{v_1+v_1}{2}F_S[/math].
- [math]v_2=v_1+\frac{F_S}{I_m}[/math] = 250 m/s + 80 m/s = 330 m/s
- [math] P=\frac{v_1+v_1}{2}F_S[/math] = 19.72 MW
- [math] F_S=(v_{2K}-v_1)\frac {I_m}{5}+(v_{2M}-v_1)\frac {4I_m}{5}[/math]. Daraus folgt [math] v_{2K}=\frac{5F_S}{4I_m}+\frac{5v_1}{4}-\frac{v_{2K}}{4}[/math] = 312.5 m/s
- [math]P =\frac 12\left(v_{2K}^2-v_1^2\right)\frac{I_m}{5}+\frac 12\left(v_{2M}^2-v_1^2\right)\frac{4I_m}{5}[/math] = 8.288 MW + 11.95 MW = 20.24 MW.
- Eine Wärmepumpe fördert Entropie. Dazu benötigt sie elektrische Energie.
- Der thermisch abgegebene Energiestrom ist 5 mal stärker als die totale Prozessleistung. Folglich beträgt die Prozessleistung 2 kW und der vom Kältebad her zufliessende Energiestrom hat eine Stärke von 8 kW.
- Der vom Kältebad zufliessende Entropiestrom hat eine Stärke von [math]I_{S1}=\frac{I_{W1}}{T_1}[/math] = 27.3 W/K. Der an den Heizwasservorlauf abfliessende Entropiestrom ist gleich [math]I_{S2}=\frac{I_{W2}}{T_2}[/math] = 31.95 W/K. Die Differenz zwischen diesen beiden Stromstärken von 4.6 W/K entspricht der Produktionsrate.
- Eine ideale Wärmepumpe benötigt eine Prozessleistung von [math] P=(T_2-T_1)I_S[/math] = 639 W. Die Differenz von 1361 W zur effektiven Leistung von 2 kW ist die Verlustleistung.
- Bei verlustfreiem, reversiblem Betrieb gilt [math] COP=\frac{I_{W2}}{P}=\frac{T_2I_S}{(T_2-T_1)I_S}=\frac{T_2}{T_2-T_1}[/math] = 15.65.
- Die von einem Körper beim isobaren Heizen oder Kühlen aufgenommene bzw. abgegebene Wärme ist gleich der Änderung der Enthalpie.
- [math]\Delta H=m\left(c_W(T_s-T_1)-q+c_E(T_2-T_s)\right)[/math] = -91.96 MJ und [math]\Delta S=m\left(c_W\ln\frac{T_s}{T_1}-\frac{q}{T_s}+c_E\ln\frac{T_2}{T_s}\right)[/math] = -335.9 kJ/K
- Die von der Wärmepumpe aufzunehmende Entropie ist gleich der vom Wasser abzugebenden Energie dividiert durch die Eingangstemperatur [math] S_{Pumpe}=\frac{\Delta H}{T_{unten}}[/math] = 378.4 kJ/K. Die aufzuwendende Pumparbeit ist dann gleich [math] W=(T_{oben}-T_{unten})S_{Pumpe}[/math] = 22.7 MJ
- Die an die Umwelt übertragene Wärme ist gleich Wth = 91.96 MJ + 22.7 MJ = 114.66 MJ. Diese Energie wird zusammen mit [math] S_{Umwelt}=\frac{W_{th}}{T_{Umwelt}}[/math] = 391.3 kJ/K der Umwelt zugeführt. Ein Vergleich mit der von der Wärmepumpe geförderten Entropie zeigt, dass 13 kJ/K produziert worden ist.
- Die Umwelt gibt weniger Entropie ab, als das Wasser aufnimmt. Der Unterschied muss produziert werden [math] S_{prod}=\Delta S-\frac{\Delta H}{T_{Umwelt}}[/math] = 335.9 kJ/K - 313.8 kJ/K = 22 kJ/K
- Mischt man heisses und kaltes Wasser, bleibt die Energie (Enthalpie) im Idealfall erhalten. Die Gesamtentropie nimmt aber in jedem Fall zu, weil bei jedem irreversiblen Vorgang Entropie erzeugt wird.
- Das heisse Wasser wird von 80°C auf 40°C abgekühlt und das kalte von 15°C auf 40°C erwärmt. Folglich beträgt der Anteil heisses Wasser 5/13 und der Anteil Kaltwasser 8/13. Die 400 Liter Boilerwasser sind demnach mit 400/5*8 = 640 Liter Kaltwasser zu mischen.
- Die dabei produzierte Entropie ist gleich [math]\Delta S=m_1 c\ln{\frac{T_m}{T_1}}+m_2 c\ln{\frac{T_m}{T_2}}[/math] = 21.66 kJ/K
- Änderungen im Heisswasser: [math]\Delta H=mc(T_m-T_1)[/math] = - 67.04 MJ und [math]\Delta S=mc\ln{\frac{T_m}{T_1}}[/math] = -201.6 kJ/K; Energieabgabe an die Umwelt [math]W_{th}=-\Delta S T_{Umwelt}[/math] = 58.06 MJ; nutzbare Energie Wnutz = 67.04 MJ - 58.06 MJ = 8.98 MJ.
- Auf das Segelflugzeug wirken das Gravitationsfeld und die Luft ein. Die Wirkung der Luft kann in eine Widerstandskraft (parallel zu Anströmung) und eine Auftriebskraft (normal zur Anströmung) zerlegt werden. Im Gleichgewichtszustand ist die Luftkraft (Summe aus Widerstand und Auftrieb) gleich der Gewichtskraft. Hier wird angenommen, dass die Beiwerte konstant sind und ein Verhältnis von 45:1 bilden. Das Flugzeug habe eine Masse von 350 kg und eine Tragfläche von 11 m2. Nimmt man an, dass die grösste Gleitzahl von 45 bei einer Geschwindigkeit von 108 km/h erreicht wird, ergibt sich ein Auftriebsbeiwert (Auftriebszahl, Auftriebskoeffizient) von 0.58. Der Widerstandsbeiwert ist dann gleich 0.013. Das Bild zeigt das Systemdiagramm (flowchart) und die Gleichungen.