Wärmekraftmaschine: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) |
||
| Zeile 15: | Zeile 15: | ||
:<math>\eta_{TD}=\frac{P}{I_{W1}}</math> |
:<math>\eta_{TD}=\frac{P}{I_{W1}}</math> |
||
Dieses Verhältnis hängt bei einer idealen, [[reversibel]] arbeitenden WKM (keine [[Entropieproduktion]]) nur noch von der Eingangs- und der Ausgangstemperatur ab |
Dieses Verhältnis, auch Carnot-Wirkungsgrad genannt, hängt bei einer idealen, [[reversibel]] arbeitenden WKM (keine [[Entropieproduktion]]) nur noch von der Eingangs- und der Ausgangstemperatur ab |
||
:<math>\ |
:<math>\eta_C=\frac{P}{I_{W1}}=\frac{(T_1-T_2)I_S}{T_1 I_S}=\frac{T_1-T_2}{T_1}</math> |
||
Ein Wirkungsgrad, der die Qualität der Wärmekraftmaschine beurteilen soll und somit alle Werte zwischen Null und eins annehmen kann, vergleicht den thermodynamischen Wirkungsgrad mit dem maximal möglichen, dem Carnot-Wirkungsgrad |
|||
:<math>\eta=\frac{\eta_{TD}}{\eta_C}</math> |
|||
==Verluste== |
==Verluste== |
||
Aktuelle Version vom 15. Juni 2008, 07:48 Uhr

Eine Wärmekraftmaschine (WKM) ist eine Maschine (Leistungswandler), die mit Wärme (Entropie) betrieben wird. Die Wirkweise einer WKM ist erstmals von Sadi Carnot erklärt worden. Carnots Idee, dass in einer WKM Wärmestoff über eine Temperaturdifferenz fällt und dabei treibende Kraft freisetzt, beschreibt exakt die Wirkweise einer idealen WKM. Nur sagt man heute Entropie statt Wärmestoff und Energie statt treibende Kraft: eine WKM überträgt die vom Entropiestrom freigesetzte Prozessleistung auf einen Impulsstrom (Kraft) oder einen Drehimpulsstrom (Drehmoment). Das Prozessschema zeigt, wie der thermisch hinunter fallende Entropiestrom eine Prozessleistung frei setzt, mit der ein Drehimpulsstrom getrieben wird. Der dem Drehimpuls zugeordnete Energiestrom heisst auch Leistung des Drehmoments.
Man unterscheidet zwischen getakteten WKM (Dampfmaschine, Ottomotor, Dieselmotor, Stirlingmotor) und kontinuierlich arbeitenden WKM (Gasturbine, Dampfturbine, Gas-Dampf-Turbine).
Wirkweise
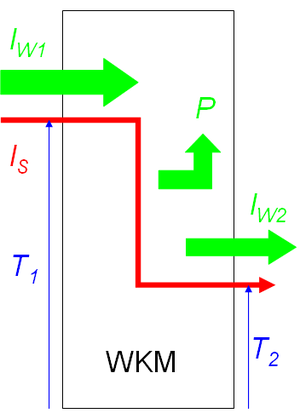
Die Wirkweise einer WKM lässt sich am besten anhand eines geschlossenen Systems (Stirlingmotor, Sekundärkreis eines Druckwasserreaktors) erklären. Bei einem solchen System tritt die Wärme (Entropie und mittransportierte Energie) über einen ersten Wärmetauscher ein und über einen zweiten wieder aus. Der bei hoher Temperatur eintretende Entropiestrom setzt einen Teil der mitgeführten Energie als Prozessleistung innerhalb der WKM frei.
Bei offenen Systemen mit interner Entropieproduktion (Ottomotor, Dieselmotor, Gasturbine) oder mit Entropiezufuhr (Dampfmaschine, Dampfturbine) setzt das Arbeitsmedium (Verbrennungsgase, Dampf) Energie frei, indem es sich ausdehnt und abkühlt. Dabei geht manifeste Entropie in latente über. Bei geschlossenem Systemen wird die Entropie über einen Wärmetauscher vom heissen System aufgenommen und ans kalte abgegeben. Dazwischen findet ebenfalls eine isentrope Expansion statt, bei dem manifeste Entropie in latente übergeführt wird. Nur muss das Arbeitsmedium nach der Entropieabgabe wieder in den heissen Zustand übergeführt werden.
Wirkungsgrad
Der thermodynamische Wirkungsgrad vergleicht die vom Entropiestrom frei gesetzte Energie mit dem thermisch zugeführten Energiestrom
- [math]\eta_{TD}=\frac{P}{I_{W1}}[/math]
Dieses Verhältnis, auch Carnot-Wirkungsgrad genannt, hängt bei einer idealen, reversibel arbeitenden WKM (keine Entropieproduktion) nur noch von der Eingangs- und der Ausgangstemperatur ab
- [math]\eta_C=\frac{P}{I_{W1}}=\frac{(T_1-T_2)I_S}{T_1 I_S}=\frac{T_1-T_2}{T_1}[/math]
Ein Wirkungsgrad, der die Qualität der Wärmekraftmaschine beurteilen soll und somit alle Werte zwischen Null und eins annehmen kann, vergleicht den thermodynamischen Wirkungsgrad mit dem maximal möglichen, dem Carnot-Wirkungsgrad
- [math]\eta=\frac{\eta_{TD}}{\eta_C}[/math]
Verluste
Energie kann unter keinen Umständen erzeugt oder vernichtet werden. Sie geht auch nicht verloren. Statt Energieverlust sollte man Entropieproduktion sagen. Wird in einem Prozess Entropie produziert, bindet die neu entstandene Entropie die im Prozess freigesetzten Energie an sich. Die von der neu entstandenen Entropie gebundene Energie nennt man dissipiert. Zwischen dissipierter Leistung und der Entropieproduktionsrate (ΠS) besteht der folgende Zusammenhang
- [math]\Pi_S=\frac{P_{diss}}{T}[/math]
Die "verlorene Energie" bleibt an der Entropie haften und kann nur freigesetzt werden, falls die Entropie erneut thermisch hinunterfällt. Um die dissipierte Energie vollständig freizusetzen, müsste die produzierte Entropie an ein System (Wärmebad)abgeführt werden, dessen Temperatur Null Kelvin beträgt.
Ersetzt man eine Wärmekraftmaschine, die zwischen einem heissen und einem kalten Wärmebad arbeitet, durch eine reine Wärmeleitung, wird die ganze Prozessleistung dissipiert. Der wegfliessende Energiestrom ist dann gleich dem zufliessenden
- [math]I_{W2}=I_{S2} T_2=(I_{S1}+\Pi_S) T_2=(I_{S1}+\frac{(T_1-T_2)I_{S1}}{T_2})T_2=T_1 I_{S1}=I_{W1}[/math]
Entropie wird bei einer WKM in den Wärmetauschern durch Wärmmeleitung und intern durch Überströmen produziert. Um diese Entropieproduktion zu minimalisieren und damit die frei verfügbare Prozessleistung zu optimieren, müssen die Wärmetauscher möglichst gross gemacht und die Druckdifferenzen beim freien Überströmen des Mediums möglichst klein gehalten werden.