Nagel einschlagen: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (Die Seite wurde neu angelegt: Der Nagel ist der wichtigste Helfer bei vielen Arbeiten mit Holz. Zimmerleute und Dachdecker nageln praktisch rund um die Uhr. Echte Nagelkünstler sind allerdings die ...) |
Admin (Diskussion | Beiträge) |
||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
==Problemstellung== |
==Problemstellung== |
||
Ein Hammer (Masse ''m<sub>1</sub>'' = 300 g) trifft mit der Geschwindigkeit ''v<sub>1</sub>'' auf einen Nagel (Durchmesser 2. 8 mm, Länge 70 mm, Masse ''m<sub>2</sub>'' = 3.5 g). Der Nagel besteht aus Eisendraht (Baustahl) der Dichte ''ρ'' = 7850 kg/m<sup>3</sup> und weist ein Elastizitätsmodul ''E'' = 2.1*10<sup>11</sup> Pa auf. Sobald der Nagel ins Holz eindringt, wirkt dieses mit einer konstanten Kraft dagegen. |
|||
Dieser Vorgang, das Einschlagen eines Nagels, soll mittels eines Simulationsmodells möglichst realistisch nachgebildet werden. |
|||
==Zweimassenschwinger== |
|||
==Zwei Körper== |
|||
Ein einfaches Modell zu diesem Problem besteht aus zwei Körpern, einer Feder und einem parallel geschalteten Dämpfer zwischen den Körpern sowie einer konstant gehaltenen Reibkraft. Nimmt man an, dass die Feder aus dem 50 mm langen Teil des Nagels besteht, der aus dem Holz ragt, erhält man eine Federkonstante von |
|||
:<math>D=\frac{AE}{L}</math> = 2.6*10<sup>7</sup> N/m |
|||
Die Schwingungsdauer der beiden Körper beträgt dann unter Vernachlässigung der Reibung |
|||
:<math>T=2\pi\sqrt{\frac{m_1m_2}{D(m_1+m_2)}}</math> = 7.27*10<sup>-5</sup> s |
|||
Wäre der Schlag vom Hammer auf den Nagel überkritisch gedämpft, würde der Nagel fast die Geschwindigkeit des Hammers erreichen |
|||
:<math>v_e=\frac{m_1}{m_1+m_2}v_1</math> |
|||
und es würden nur etwas mehr als 1% der kinetischen Energie dissipiert |
|||
:<math>W_{diss}=\Delta p \Delta v_{mittel}=(v_1-v_e)m_1\frac{v_1}{2}=\frac{m_2}{m_1m_2}W_{kin}</math> = 0.0115 ''W<sub>kin</sub>'' |
|||
Die kritische Dämpfung kann mit einer Dämpferkonstante von |
|||
:<math>k=2\sqrt{\frac{m_1m_2}{m_1+m_2}D}</math> = 600 Ns/m |
|||
erzielt werden. Zur Abschätzung der Reibkraft vernachlässigen wir die [[Dissipation]] zwischen Hammer und Nagel. Die Reibarbeit ist dann gleich der [[kinetische Energie|kinetischen Energie]] des Hammers. Damit ergibt sich die Reibkraft aus der Eindringtiefe ''s'' |
|||
:<math>F_R=\frac{m_1v_1^2}{2s}</math> |
|||
Die nachfolgenden Abbildungen zeigen das [[Systemdiagramm]] (flowchart), das Geschwindigkeits-Zeit-Verhalten von Hammer und Nagel während den ersten 5 ms und das Kraft-Zeit-Verhalten in den ersten 0.1 ms mit einer Anfangsgeschwindigkeit von 10 m/s und einem konstanten Impulsfluss von 750 N zwischen Nagel und Holz. |
|||
<gallery> |
|||
Bild:Nageln SD.jpg|Systemdiagramm mit Gleichungen |
|||
Bild:Nageln v-t-D.png|''v-t-''Diagramm während 5 ms |
|||
Bild:Nageln F-t-D.png|''F-t-''Diagramm während 0.1 ms |
|||
</gallery> |
|||
Lässt man die Dämpfung weg, prellt der Hammer mehrmals gegen den Nagel (1. und 2. Bild). Verzehnfacht man die Kraft, mit welcher der Nagel auf das Holz einwirkt, wird der Hammer zurück geworfen (3. Bild) |
|||
<gallery> |
|||
Bild:Nageln v-t-D2.png|''v-t-''Diagramm ohne Dämpfung |
|||
Bild:Nageln F-t-D2.png|''F-t-''Diagramm ohne Dämpfung |
|||
Bild:Nageln v-t-D3.png|''v-t-''mit hartem Holz |
|||
</gallery> |
|||
Die Dynamik des Nagel einschlagens kann mit einem Zweikörper-Modell befriedigend nachgebildet werden, falls man eine optimale Dämpfer-Konstante einführt. Die Dämpferkraft steigt dann im ersten Moment auf etwa das Achtfache der Kraft, mit welcher der Nagel auf das Holz einwirkt. Doch die zentrale Frage, wie ein Nagel, der in guter Näherung ein linear-elastisches Verhalten zeigt, eine dermassen starke Dämpfung aufbauen kann, lässt sich mit einem solch einfachen Modell nicht beantworten. |
|||
==Federkette== |
==Federkette== |
||
Aktuelle Version vom 17. Juni 2008, 05:19 Uhr
Der Nagel ist der wichtigste Helfer bei vielen Arbeiten mit Holz. Zimmerleute und Dachdecker nageln praktisch rund um die Uhr. Echte Nagelkünstler sind allerdings die Einschaler, also Tischler, die Holzverschalungen für den Betonbau herstellen. Diese beherrschen die Kunst, Nägel bewusst krumm einzuschlagen, um extrem belast- und fast unlösbare Nagelverbindungen herzustellen, wie niemand sonst. Doch wie steht es mit der Physik des Nagelns? Lässt sich das Problem einfach modellieren und simulieren?
Problemstellung
Ein Hammer (Masse m1 = 300 g) trifft mit der Geschwindigkeit v1 auf einen Nagel (Durchmesser 2. 8 mm, Länge 70 mm, Masse m2 = 3.5 g). Der Nagel besteht aus Eisendraht (Baustahl) der Dichte ρ = 7850 kg/m3 und weist ein Elastizitätsmodul E = 2.1*1011 Pa auf. Sobald der Nagel ins Holz eindringt, wirkt dieses mit einer konstanten Kraft dagegen.
Dieser Vorgang, das Einschlagen eines Nagels, soll mittels eines Simulationsmodells möglichst realistisch nachgebildet werden.
Zwei Körper
Ein einfaches Modell zu diesem Problem besteht aus zwei Körpern, einer Feder und einem parallel geschalteten Dämpfer zwischen den Körpern sowie einer konstant gehaltenen Reibkraft. Nimmt man an, dass die Feder aus dem 50 mm langen Teil des Nagels besteht, der aus dem Holz ragt, erhält man eine Federkonstante von
- [math]D=\frac{AE}{L}[/math] = 2.6*107 N/m
Die Schwingungsdauer der beiden Körper beträgt dann unter Vernachlässigung der Reibung
- [math]T=2\pi\sqrt{\frac{m_1m_2}{D(m_1+m_2)}}[/math] = 7.27*10-5 s
Wäre der Schlag vom Hammer auf den Nagel überkritisch gedämpft, würde der Nagel fast die Geschwindigkeit des Hammers erreichen
- [math]v_e=\frac{m_1}{m_1+m_2}v_1[/math]
und es würden nur etwas mehr als 1% der kinetischen Energie dissipiert
- [math]W_{diss}=\Delta p \Delta v_{mittel}=(v_1-v_e)m_1\frac{v_1}{2}=\frac{m_2}{m_1m_2}W_{kin}[/math] = 0.0115 Wkin
Die kritische Dämpfung kann mit einer Dämpferkonstante von
- [math]k=2\sqrt{\frac{m_1m_2}{m_1+m_2}D}[/math] = 600 Ns/m
erzielt werden. Zur Abschätzung der Reibkraft vernachlässigen wir die Dissipation zwischen Hammer und Nagel. Die Reibarbeit ist dann gleich der kinetischen Energie des Hammers. Damit ergibt sich die Reibkraft aus der Eindringtiefe s
- [math]F_R=\frac{m_1v_1^2}{2s}[/math]
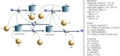
Die nachfolgenden Abbildungen zeigen das Systemdiagramm (flowchart), das Geschwindigkeits-Zeit-Verhalten von Hammer und Nagel während den ersten 5 ms und das Kraft-Zeit-Verhalten in den ersten 0.1 ms mit einer Anfangsgeschwindigkeit von 10 m/s und einem konstanten Impulsfluss von 750 N zwischen Nagel und Holz.
-
Systemdiagramm mit Gleichungen
-
v-t-Diagramm während 5 ms
-
F-t-Diagramm während 0.1 ms
Lässt man die Dämpfung weg, prellt der Hammer mehrmals gegen den Nagel (1. und 2. Bild). Verzehnfacht man die Kraft, mit welcher der Nagel auf das Holz einwirkt, wird der Hammer zurück geworfen (3. Bild)
-
v-t-Diagramm ohne Dämpfung
-
F-t-Diagramm ohne Dämpfung
-
v-t-mit hartem Holz
Die Dynamik des Nagel einschlagens kann mit einem Zweikörper-Modell befriedigend nachgebildet werden, falls man eine optimale Dämpfer-Konstante einführt. Die Dämpferkraft steigt dann im ersten Moment auf etwa das Achtfache der Kraft, mit welcher der Nagel auf das Holz einwirkt. Doch die zentrale Frage, wie ein Nagel, der in guter Näherung ein linear-elastisches Verhalten zeigt, eine dermassen starke Dämpfung aufbauen kann, lässt sich mit einem solch einfachen Modell nicht beantworten.