Aviatik 2007/Ass: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 39: | Zeile 39: | ||
==Aufgabe 3== |
==Aufgabe 3== |
||
Das |
[[Bild:Aviatik 07 Ass 3.png|thumb|Fussball]]Das rechts abgebildete Diagramm zeigt die beiden Geschwindigkeits-Zeit-Diagramme (Horizontal- und Vertikalkomponente) eines Fussballs (Masse 440 g), der von Torwart ab Boden mit einer Geschwindigkeit von 30 m/s unter einem Winkel von 45° abgeschossen wird. |
||
#Wie hoch steigt der Ball auf (höchster Punkt der Wurfbahn)? |
#Wie hoch steigt der Ball auf (höchster Punkt der Wurfbahn)? |
||
#Wie gross ist die Beschleunigung des Balls am höchsten Punkt? |
#Wie gross ist die Beschleunigung des Balls am höchsten Punkt? |
||
| Zeile 67: | Zeile 67: | ||
==Aufgabe 7== |
==Aufgabe 7== |
||
In einer sonst leeren Kühlbox liegt eine mit Eis |
In einer sonst leeren Kühlbox liegt eine mit Eis gefüllte PET-Flasche. Man stellt fest, dass die Innentemperatur der Box bei einer Aussentemperatur von 25° auf 14° C absinkt und dass pro Stunde 50 g Eis abschmelzen. |
||
#Wie gross ist der Wärmeleitwert der Box? |
#Wie gross ist der Wärmeleitwert der Box? |
||
#Die Box wird nun in ein an der Sonne stehendes Auto gestellt (Innentemperatur 50°C). Es ist zu vermuten, dass die Temperatur im Innern der Box auf 28°C steigt und dass pro Stunde 100 g Eis abschmelzen. Stimmt diese Behauptung? Geben Sie eine physikalisch begründete Antwort! |
#Die Box wird nun in ein an der Sonne stehendes Auto gestellt (Innentemperatur 50°C). Es ist zu vermuten, dass die Temperatur im Innern der Box auf 28°C steigt und dass pro Stunde 100 g Eis abschmelzen. Stimmt diese Behauptung? Geben Sie eine physikalisch begründete Antwort! |
||
| Zeile 73: | Zeile 73: | ||
==Aufgabe 8== |
==Aufgabe 8== |
||
Ein Elektromotor |
Ein Elektromotor treibt über eine Rutschkupplung einen Bohrkopf an. Der geregelte Motor läuft mit einer konstanten [[Winkelgeschwindigkeit]] von 4000 U/min. Der Bohrkopf bohrt nicht dauernd, sondern wird vom Werkstück zurückgezogen, sobald seine Drehzahl unter 2000 U/min sinkt. Das gibt einen intervallweisen Bearbeitungsablauf mit zwei Phasen: |
||
*Phase 1: Bohrkopf beschleunigt ohne Bohren |
|||
| ⚫ | |||
*Phase 2: Borhkopf bohrt und wird über Rutschkupplung angetrieben |
|||
#Wie gross ist der Drehimpuls von Schwungrad-Teil und Bohrkopf-Teil zu Beginn und am Ende der Bohrphase? |
|||
Während des Beschleunigens steigt die Drehzahl des Bohrkopfs in 5 s von 2000 U/min auf 4000 U/min. Beim Bohren sinkt sie dann in weiteren 5 s wieder auf 2000 U/min ab. Über die die Rutschkupplung fliesst ein konstanter Drehimpulsstrom von 20 Nm. Der Drehimpulsstrom von Bohrkopf zu Werkstück ist während der Bohrphase ebenfalls konstant.. |
|||
#Wie lange dauert die Bohrphase? |
|||
| ⚫ | |||
#Wie viel Energie wird in der Rutschkupplung dissipiert? |
|||
#Berechnen Sie das [[Massenträgheitsmoment]] des Bohrkopfs. |
|||
#Berechnen Sie das Reibmoment zwischen Bohrkopf und Werkstück. |
|||
#Berechenen Sie die Prozessleistung in der Rutschkupplung und im Bohrprozess für den Zeitpunkt 6 s. |
|||
==Aufgabe 9== |
|||
[[Bild:Aviatik 07 Ass 4.png|thumb|Bugrad]] Während einer notfallmässigen Landung löst sich kurz nach einem harten Aufsetzen das Bugrad (Durchmesser 1.2 m, Masse 100 kg, [[Massenträgheitsmoment]] 15 kgm<sup>2</sup>). Unmittelbar danach rutscht es mit einer Geschwindigkeit von 70 m/s und einer [[Winkelgeschwindigkeit]] von 20 s<sup>-1</sup> über die Piste. Die Gleitreibung hat einen Koeffizienten von 0.6. |
|||
#Zeichnen Sie ein [[freischneiden|Schnittbild]] des Bugrades (Kräfte einzeichnen). |
|||
#Stellen Sie die Grundgesetze für das Bugrad auf (Bilanzen von [[Impuls]] und [[Drehimpuls]]). |
|||
#Berechnen Sie die [[Beschleunigung]] und die [[Winkelbeschleunigung]] des Bugrades. |
|||
#Berechnen Sie die [[Geschwindigkeit]], mit der das Rad schliesslich über die Piste rollt. |
|||
'''[[Lösungen zu Aviatik 2007/Ass|Lösungen]]''' |
'''[[Lösungen zu Aviatik 2007/Ass|Lösungen]]''' |
||
Aktuelle Version vom 24. Juli 2009, 06:58 Uhr
Erlaubte Hilfsmittel: Taschenrechner, selbstverfasste Formelsammlung
Daten:
| Gravitationsfeldstärke | 9.81 N/kg |
| spez. Wärmekapazität von Wasser | 4.19 kJ/(kg K) |
| spez. Wärmekapazität von Eis | 2.1 kJ/(kg K) |
| spez. Schmelzenthalpie von Eis | 334 kJ/kg |
| Verdampfungsenthalpie von Wasser | 2256 kJ/kg |
| Anzahl Freiheitsgrade der Luftmoleküle | 5 |
| universelle Gaskonstante R | 8.314 J/(mol K) |
Aufgabe 1
Modellieren Sie folgendes Experiment: 2 Gefässe sind an ihrem Boden mit einem dünnen Schlauch verbunden. Das eine ist zu Beginn leer, das andere voll. Der Sockel in der Zeichnung wird nur in d) gebraucht. Mit einem Hahn im Schlauch startet man den Flüssigkeitsausgleich zwischen den Gefässen. Im Schlauch stellt sich eine laminare Strömung ein. Die Daten des Experimentes: Grundfläche Gefäss eins 2 dm2, Startvolumen 0; Grundfläche Gefäss zwei 3 dm2, Startvolumen 4 Liter; hydraulischer Widerstand des Schlauchs 4 * 1010 Pa s/m3.
- Ergänzen Sie das angefangene Flowchart mit allen notwendigen Variablen.
- Definieren Sie alle Variablen mit ihren Gleichungen oder festen Werten.
- Modellieren Sie auch die Energie, die im Schlauch dissipiert wird. Ergänzen Sie dazu das Flowchart und die Gleichungen.
- Das Experiment wird leicht verändert: Gefäss 1 wird auf einen 10 cm hohen Sockel gestellt. Passen Sie das Flowchart und die Gleichungen an. Sie können das mit einer anderen Stiftfarbe (aber nicht mit rot) in den Lösungen von 1) bis 3) tun.
Aufgabe 2
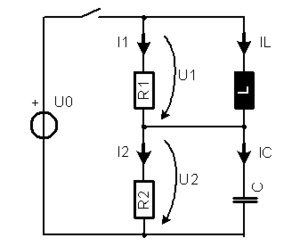
An einem Spannungsteiler sind eine ideale Spule und ein Kondensator angeschlossen (siehe Zeichnung). Die Elemente haben folgende Werte: U0 = 5 V, R1 = 20 kΩ, R2 = 10 kΩ, L = 4 mH, C = 10 μF.
- Berechnen Sie die Spannungen U1 und U2 und die Ströme I1 bis I4 für einen Zeitpunkt kurz nach dem Einschalten.
- Berechnen Sie die Werte für die selben Grössen lange danach.
- Berechnen Sie für den selben Zeitpunkt wie in 1) den Energiestrom, der die Spannungsquelle verlässt, und die dissipierte Leistung.
Aufgabe 3
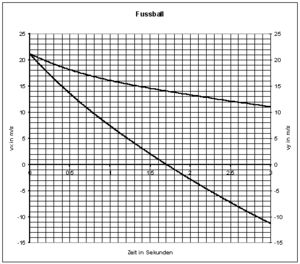
Das rechts abgebildete Diagramm zeigt die beiden Geschwindigkeits-Zeit-Diagramme (Horizontal- und Vertikalkomponente) eines Fussballs (Masse 440 g), der von Torwart ab Boden mit einer Geschwindigkeit von 30 m/s unter einem Winkel von 45° abgeschossen wird.
- Wie hoch steigt der Ball auf (höchster Punkt der Wurfbahn)?
- Wie gross ist die Beschleunigung des Balls am höchsten Punkt?
- Wie stark ist der Luftwiderstand am höchsten Punkt?
- Welche Leistung wird am höchsten Punkt dissipiert?
Aufgabe 4
Ein Flugzeug (Masse 25 Tonnen) fliegt mit 900 km/h auf einer horizontalen Kreisbahn. Die Fügelebene ist um 50° gegen die Horizontale geneigt.
- Wie stark ist die Auftriebskraft auf das Flugzeug.
- Wie lange dauert es, bis das Flugzeug einen Halbkreis geflogen ist?
- Mit welcher Kraft wirkt das Flugzeug auf den Piloten (Masse 75 kg) ein?
- Wie stark ist das im System Flugzeug messbare Gravitationsfeld?
Aufgabe 5
Fünf Meter unterhalb seiner Wasseroberfläche weist ein Tank ein seitlich angebrachtes Loch (Querschnitt 50 mm2) auf, das vorerst mit einem zylinderförmigen Kolben verschlossen ist.
- Mit welcher Kraft muss der Kolben festgehalten werden?
- Wie schnell fliesst das Wasser nach dem Entfernen des Kolbens aus dem Loch horizontal weg?
- Der Querschnitt des Wasserstrahls ist kleiner als das Loch. Wie gross müsste der Querschnitt sein, damit der vom Wasser konvektiv transportierte Impulsstrom gleich stark ist wie der vorher leitungsartig durch den Kolben geflossene Impulsstrom (der allseits wirkende Druck der umgebenden Luft ist zu vernachlässigen)?
- Wie stark ist dann der vom Wasser transportierte Energiestrom (nur kinetische Energie)?
Aufgabe 6
Der idealisierte Otto-Zyklus (reversibel, mit reiner Luft gerechnet) soll nachfolgend diskutiert werden. Die Luft wird zuerst isentropen auf 15 bar komprimiert und danach isochor auf 1927°C geheizt. Nachfolgend wird die Luft isentrop auf das ursprüngliche Volumen expandiert und danach isochor auf den Anfangszustand gekühlt. Der Kreisprozess startet bei einem Absolutdruck von einem Bar, einem Volumen von drei Liter und einer Temperatur von 27°C. Die Luft verhalte sich wie ein zweiatomiges, ideales Gas.
- Skizzieren Sie das T-S- sowie das p-V-Diagramm qualitativ richtig (ohne Massangaben, gekrümmte Kurven sollten aber als solche erkennbar sein).
- Wie hoch steigt die Temperatur bei der isentropen Kompression?
- Wie gross sind Druck und Temperatur nach der isentropen Expansion?
- Wie viel Energie wird pro Zyklus netto in Form von Arbeit abgegeben?
Aufgabe 7
In einer sonst leeren Kühlbox liegt eine mit Eis gefüllte PET-Flasche. Man stellt fest, dass die Innentemperatur der Box bei einer Aussentemperatur von 25° auf 14° C absinkt und dass pro Stunde 50 g Eis abschmelzen.
- Wie gross ist der Wärmeleitwert der Box?
- Die Box wird nun in ein an der Sonne stehendes Auto gestellt (Innentemperatur 50°C). Es ist zu vermuten, dass die Temperatur im Innern der Box auf 28°C steigt und dass pro Stunde 100 g Eis abschmelzen. Stimmt diese Behauptung? Geben Sie eine physikalisch begründete Antwort!
- Statt mit Eis soll die Box im Auto nun mit einer Wärmepumpe gekühlt werden. Wir modellieren die Wärmepumpe als ideale Pumpe, welche die Wärme bei 0°C aufnimmt und bei 60°C abgibt. Welche Leistung muss die Wärmepumpe aufnehmen?
Aufgabe 8
Ein Elektromotor treibt über eine Rutschkupplung einen Bohrkopf an. Der geregelte Motor läuft mit einer konstanten Winkelgeschwindigkeit von 4000 U/min. Der Bohrkopf bohrt nicht dauernd, sondern wird vom Werkstück zurückgezogen, sobald seine Drehzahl unter 2000 U/min sinkt. Das gibt einen intervallweisen Bearbeitungsablauf mit zwei Phasen:
- Phase 1: Bohrkopf beschleunigt ohne Bohren
- Phase 2: Borhkopf bohrt und wird über Rutschkupplung angetrieben
Während des Beschleunigens steigt die Drehzahl des Bohrkopfs in 5 s von 2000 U/min auf 4000 U/min. Beim Bohren sinkt sie dann in weiteren 5 s wieder auf 2000 U/min ab. Über die die Rutschkupplung fliesst ein konstanter Drehimpulsstrom von 20 Nm. Der Drehimpulsstrom von Bohrkopf zu Werkstück ist während der Bohrphase ebenfalls konstant..
- Skizzieren Sie das Drehimpuls-Flüssigkeitsbild für die Zeitpunkte 2 und 6 s.
- Berechnen Sie das Massenträgheitsmoment des Bohrkopfs.
- Berechnen Sie das Reibmoment zwischen Bohrkopf und Werkstück.
- Berechenen Sie die Prozessleistung in der Rutschkupplung und im Bohrprozess für den Zeitpunkt 6 s.
Aufgabe 9
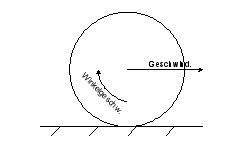
Während einer notfallmässigen Landung löst sich kurz nach einem harten Aufsetzen das Bugrad (Durchmesser 1.2 m, Masse 100 kg, Massenträgheitsmoment 15 kgm2). Unmittelbar danach rutscht es mit einer Geschwindigkeit von 70 m/s und einer Winkelgeschwindigkeit von 20 s-1 über die Piste. Die Gleitreibung hat einen Koeffizienten von 0.6.
- Zeichnen Sie ein Schnittbild des Bugrades (Kräfte einzeichnen).
- Stellen Sie die Grundgesetze für das Bugrad auf (Bilanzen von Impuls und Drehimpuls).
- Berechnen Sie die Beschleunigung und die Winkelbeschleunigung des Bugrades.
- Berechnen Sie die Geschwindigkeit, mit der das Rad schliesslich über die Piste rollt.