Lösungen zu Aviatik 2007/Ass: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
|||
| (4 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 49: | Zeile 49: | ||
#Die beiden Diagramme können unter dem Thema [[Otto-Zyklus]] aufgerufen werden. |
#Die beiden Diagramme können unter dem Thema [[Otto-Zyklus]] aufgerufen werden. |
||
#Das komprimierte Volumen ist gleich <math>V_2=V_1\left(\frac{p_1}{p_2}\right)^{1/\kappa}</math> = 0.434 Liter. Für diesen Wert liefert die ideale Gasgleichung <math>T_2=T_1\frac{p_2V_2}{p_1V_1}</math> = 650 K |
#Das komprimierte Volumen ist gleich <math>V_2=V_1\left(\frac{p_1}{p_2}\right)^{1/\kappa}</math> = 0.434 Liter. Für diesen Wert liefert die ideale Gasgleichung <math>T_2=T_1\frac{p_2V_2}{p_1V_1}</math> = 650 K |
||
#Zu Beginn der isentropen Expansion ist das Volumen immer noch 0.434 Liter, die Temperatur aber |
#Zu Beginn der isentropen Expansion ist das Volumen immer noch 0.434 Liter, die Temperatur aber auf 2200 K gestiegen. Statt in zwei Schritten wie unter 2. rechnen wir diesmal die Temperatur direkt in einem Schritt aus <math>T_4=T_3\left(\frac{V_3}{V_4}\right)^{\kappa-1}</math> = 1015 K |
||
#Die Nettoarbeit entspricht der ausgeschnittenen Fläche im ''T-S-'' oder im ''p-V-''Diagramm. Man kann |
#Die Nettoarbeit entspricht der ausgeschnittenen Fläche im ''T-S-'' oder im ''p-V-''Diagramm. Man kann die gesuchte Energie somit über die zu- und abgeführt Wärme oder über die Kompressions- und Expansionsarbeit berechnen. Nun ist die Expansionsarbeit bei der isentropen Expansion gleich der Änderung der inneren Energie. Deshalb gilt <math>W=n\hat c_V(T_3-T_4-(T_2-T_1))=n\frac 52 R(T_3-T_4-T_2+T_1)=\frac 52\frac{p_1V_1}{T_1}(1185K-350K)</math> = 2088 J. |
||
==Aufgabe 7== |
==Aufgabe 7== |
||
#Der von aussen in die Kühlbox fliessende Energiestrom hat eine Stärke von <math>I_W=\frac{\Delta mq}{\Delta t}</math> = 4.64 W. Folglich ist der Wärmeleitwert gleich <math>G_W=\frac{I_W}{\Delta T}</math> = 0.422 W/K. |
|||
#Box und Flasche (inkl. Wärmeübergänge) bilden bezüglich des Wärmeenergiestromes eine Serieschaltung von zwei Leitwerten. Geht man nun davon aus, dass die Leitwerte nicht vom Wärmestrom abhängen, teilen sie die Temperaturdifferenz zwischen aussen und innen (Eiswasser von 0°C) immer im gleichen Verhältnis. Zudem führt ein doppelt so grosses Temperaturgefälle zu einem doppelt so starken Wärmestrom. |
|||
#Der von aussen zufliessende Wärmeenergiestrom ist gleich <math>I_W=G_W\Delta T</math> = 9.28 W. Dies ergibt am Ort des Eis-Wasser-Gemisches einen zufliessenden Entropiestrom der Stärke <math>I_S=\frac{I_W}{T_s}=\frac{9.28W}{273K}</math> = 0.034 W/K. Um diesen Entropiestrom um 60 K hinauf zu pumpen, benötigt man eine Prozessleistung von <math>P=\Delta TI_S</math> = 2.04 W. |
|||
==Aufgabe 8== |
==Aufgabe 8== |
||
Das zu betrachtende System besteht aus nur einem Drehimpulsspeicher, dem Bohrkopf mit Bohrer. Vom Motor her fliesst ein konstanter Drehimpulsstrom zu. Der an das Werkstück weg fliessende Drehimpulsstrom wird in Abständen von fünf Sekunden ein- und ausgeschaltet. |
|||
#Das [[Flüssigkeitsbild]] besteht aus einem Topf, welcher für den Bohrkopf steht. Zum Zeitpunkt 2 s fliesst vom Motor her (Füllhöhe 419 1/s) ein [[Drehimpulsstrom]] der Stärke 20 Nm in den Topf (momentane Füllhöhe 293 1/s). Zum Zeitpunkt 6 s strömt immer noch [[Drehimpuls]] der Stärke 20 Nm zu. Zusätzlich fliesst noch ein Strom unbekannter Stärke weg. Die Füllhöhe beträgt nun 377 1/s. |
|||
#In 5 s fliessen 5 * 20 Nm = 100 Nms [[Drehimpuls]] zu. Gleichzeitig ändert sich die [[Winkelgeschwindigkeit]] um Δω = 209 1/s. Dies ergibt für das [[Massenträgheitsmoment]] einen Wert von <math>J=\frac{\Delta L}{\Delta \omega}</math> = 0.478 kgm<sup>2</sup>. |
|||
#Aus der Drehimpulsbilanz <math>M_R-M_B=\dot L</math> folgt <math>M_B=M_R-\dot L=M_R-\frac{\Delta L}{\Delta t}</math> = 40 Nm. |
|||
#Die [[Prozessleistung]] ist gleich Stromstärke mal Potenzialdifferenz, als gleich Drehmoment mal Differenz der Winkelgeschwindigkeit |
|||
:*''P<sub>R</sub>'' = 20 Nm * 41.9 1/s = 838 W |
|||
:*''P<sub>B</sub>'' = 40 Nm * 377 1/s = 15.1 kW |
|||
==Aufgabe 9== |
==Aufgabe 9== |
||
Das Bugrad hat am untersten Punkt eine Geschwindigkeit von <math>v=v_M-\omega r</math> = 58 m/s nach rechts. Folglich wirkt die Gleitreibung nach links. |
|||
#Auf das Bugrad wirken die Gewichtskraft, eine Normalkraft sowie eine Gleitreibungskraft (nach links) ein. |
|||
#Die drei Bilanzgleichungen (Grundgesetze) lauten (''x''-Achse nach rechts, ''y''-Achse nach unten, positive Drehrichtung im Uhrzeigersinn) |
|||
##''x'': <math>-F_R=\dot p_x=m\dot v_x</math> |
|||
##''y'': <math>F_G-F_N=\dot p_y</math> |
|||
##''R'': <math>F_Rr=\dot L=J\dot\omega</math> |
|||
#In der Rutschphase sind die alle drei Bilanzgleichungen geometrisch entkoppelt. Deshalb können beide Fragen getrennt beantwortet werden |
|||
##<math>\dot v_x=-\frac{F_R}{m}=-\frac{\mu mg}{m}=-\mu g</math> = -5.89 m/s<sup>2</sup> |
|||
##<math>\dot \omega=\frac{F_Rr}{J}=\frac{\mu mgr}{J}</math> = 23.5 1/s |
|||
#Die Lösung zu dieser Teilaufgabe ist unter [[Bowling]] ausgiebig besprochen. Die entscheidende Idee lautet |
|||
:*<math>\frac{F_Rr}{F_R}=\frac{|\Delta L|}{|\Delta p|}=\frac{J(\omega_e-\omega_a)}{m(v_a-v_e)}</math> woraus folgt |
|||
:*<math>v_e=\frac{mrv_a+J\omega_0}{\frac{J}{r}+mr}</math> = 53 m/s |
|||
'''[[Aviatik 2007/Ass|Aufgabe]]''' |
'''[[Aviatik 2007/Ass|Aufgabe]]''' |
||
Aktuelle Version vom 23. August 2010, 06:47 Uhr
Aufgabe 1
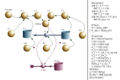
Das erste Bild zeigt das Systemdiagramm und die Gleichungen zur gesamten Aufgabe. Im zweiten Bild ist der Volumenstrom und der Druck in beiden Gefässen bezogen auf einen gemeinsamen Nullpunkt dargestellt. Dieses Problem ist auch geschlossen lösbar. Um die Simulationszeit zu berechnen, rechnet man mit Vorteil die Zeitkonstante aus
- [math]\tau=RC[/math] = 4.89 104 s mit [math]C=\frac{C_1C_2}{C_1+C_2}=\frac{A_1A_2}{A_1+A_2}\frac{1}{\varrho g}[/math] = 1.22 10-6 m3/Pa
-
Systemdiagramm
-
Volumenstrom und Druck
Aufgabe 2
Eine Kondensator verhält sich im ersten Moment wie ein Kurzschluss und nach langer Zeit wie ein offener Schalter. Die ideale Spule wirkt genau umgekehrt. Deshalb fliesst der Strom im ersten Moment durch R1 und durch C. Nach langer Zeit geht der Strom durch L und durch R2.
- Unmittelbar nach dem Schliessen des Schalters gilt: U1 = U0; U2 = 0;IL = I2 = 0; [math]I_C=I_1=\frac{U_0}{R_1}[/math] = 0.25 mA;
- Längere Zeit danach gilt: U2 = U0; U1 = 0;IC = I1 = 0; [math]I_L=I_2=\frac{U_0}{R_2}[/math] = 0.5 mA;
- Der Energiestrom, der die Spannungsquelle verlässt, geht vollständig in das Widerstandselement 1 hinein und wird dort dissipiert. Die Energiestromstärke ist deshalb gleich der Prozessleistung im Widerstandselement 1: [math]I_W=P=U_1I_1=\frac{U_0^2}{R_1}[/math] = 1.25 mW.
Aufgabe 3
Auf den Fussball wirken nach dem Abschuss die Gewichtskraft und der Luftwiderstand ein.
- Die Wurfhöhe entspricht der Fläche unter dem vy-t-Diagramm, also etwa 16.5 m.
- Die Horizontal- und die Vertikalbeschleunigung findet man als Steigung der entsprechenden Geschwindigkeits-Kurven. Weil der Luftwiderstand genau horizontal wirkt, ist die Vertikalbeschleunigung gleich der Gravitationsfeldstärke. Die Betrag der Beschleunigung ist demnach gleich [math]a=\sqrt{a_x^2+a_y^2}=\sqrt{2.5^2+9.81^2} m/s^2[/math] = 10.1 m/2.
- Im höchsten Punkt ist der Lufwiderstand gleich Masse des Balls mal Horizontalbeschleungigung: [math]F_W=ma_x[/math] = 1.13 N.
- Die dissipierte Leistung ist gleich Luftwiderstand mal Horizontalgeschwindigkeit, also gleich [math]P(F_W)=v_xF_W[/math] = 14 m/s*1.13 N = 15.8 W.
Aufgabe 4
Auf das Flugzeug wirken nur die Gewichtskraft, die umgebende Luft und die Triebwerke ein. Die Wirkung der Luft zerlegt man in Widerstand (parallel zur Anströmung) und dynamischen Auftrieb (normal zur Anströmung). Nimmt man zudem an, dass der Auftrieb normal zur Flügelebene steht, ist diese Aufgabe lösbar. Nun erzeugen Auftrieb und Gewichtskraft die Normalbeschleunigung, die gegen die Kurvenmitte gerichtet ist. Folglich gilt:
- [math]F_A\sin\alpha=ma_n[/math]
- [math]F_G-F_A\cos\alpha=0[/math] oder [math]F_A\cos\alpha=mg[/math]
Die Lösung dieses Gleichungssystems liefert
- [math]a_n=g\tan\alpha[/math]
- [math]F_A=\frac{mg}{\cos\alpha}[/math] = 382 kN
- Die halbe Umlaufzeit ist gleich halber Kreisumfang durch Schnelligkeit [math]\frac{T}{2}=\frac{\pi r}{v}[/math]. Nun ersetzen wir den Radius durch [math]r=\frac{v^2}{a_n}[/math] und formen die Normalbeschleunigung mit der weiter oben gefundenen Formel um [math]\frac T2=\frac{\pi v}{a_n}=\frac{\pi v}{g\tan\alpha}[/math] = 67.2 s.
- Auf den Piloten wirken das Gravitationsfeld und das Flugzeug ein. Zusammen erzeugen sie die Beschleunigung des Piloten. Folglich können die vorher gemachten Überlegungen vom Flugzeug auf den Piloten übertragen werden: [math]F_{Flugzeug}=\frac{m_{Pilot}g}{\cos\alpha}[/math] = 1145 N
- Im System Flugzeug ist neben dem allgegenwärtigen, fast homogenen Feld der Erde noch ein Trägheitsfeld - oder etwas präziser ausgedrückt - ein Zentrifugalfeld nachweisbar. Direkt messbar ist aber nur die Superposition dieser beiden Felder (homogenes Feld nach unten, zylindersymmetrisches Feld nach aussen). Zur Superposition müssen die Feldstärken in jedem Punkt des Raumes vektoriell addiert werden, was im Mittelpunkt des Flugzeuges folgenden Betrag ergibt [math]g'=\sqrt{g^2+g_z^2}=\sqrt{g^2+a_n^2}= g\sqrt{1+\tan^2\alpha}[/math] = 15.3 N/kg
Aufgabe 5
- Auf den Kolben wirkt ein resultierende Druckkraft nach aussen [math]F_K=A_K\varrho gh[/math] = 2.45 N
- Hier kann direkt das Ausflussgesetz von Torricelli verwendet werden: [math]v=\sqrt{2gh}[/math] = 9.9 m/s
- Der Querschnitt des Wasserstrahls ist bei scharfkantigem Ausfluss kleiner als die Bohrung. Aus [math]I_{p,conv}=vI_m=\varrho v^2A_{Strahl}=\varrho 2ghA_{Strahl}=F_K=A_K\varrho gh[/math] folgt [math]A_{Strahl}=\frac{A_K}{2}[/math] = 25 mm2
- Die Stärke des vom Wasserstrahl mitgeführten Energiestromes ist gleich [math]I_{W_{kin}}=\frac{\varrho}{2}v^2I_V=\varrho ghv A_{Strahl}=\frac{F_K}{2}v[/math] = 12.1 W.
Aufgabe 6
Der Otto-Zyklus ist der Grenzprozess, der in Otto-Motoren im Rahmen des technisch Möglichen realisiert ist. Die Stoffmenge ist durch die Anfangsbedingungen festgelegt
- [math]n=\frac{p_1V_1}{RT_1}[/math] = 0.12 mol
- Die beiden Diagramme können unter dem Thema Otto-Zyklus aufgerufen werden.
- Das komprimierte Volumen ist gleich [math]V_2=V_1\left(\frac{p_1}{p_2}\right)^{1/\kappa}[/math] = 0.434 Liter. Für diesen Wert liefert die ideale Gasgleichung [math]T_2=T_1\frac{p_2V_2}{p_1V_1}[/math] = 650 K
- Zu Beginn der isentropen Expansion ist das Volumen immer noch 0.434 Liter, die Temperatur aber auf 2200 K gestiegen. Statt in zwei Schritten wie unter 2. rechnen wir diesmal die Temperatur direkt in einem Schritt aus [math]T_4=T_3\left(\frac{V_3}{V_4}\right)^{\kappa-1}[/math] = 1015 K
- Die Nettoarbeit entspricht der ausgeschnittenen Fläche im T-S- oder im p-V-Diagramm. Man kann die gesuchte Energie somit über die zu- und abgeführt Wärme oder über die Kompressions- und Expansionsarbeit berechnen. Nun ist die Expansionsarbeit bei der isentropen Expansion gleich der Änderung der inneren Energie. Deshalb gilt [math]W=n\hat c_V(T_3-T_4-(T_2-T_1))=n\frac 52 R(T_3-T_4-T_2+T_1)=\frac 52\frac{p_1V_1}{T_1}(1185K-350K)[/math] = 2088 J.
Aufgabe 7
- Der von aussen in die Kühlbox fliessende Energiestrom hat eine Stärke von [math]I_W=\frac{\Delta mq}{\Delta t}[/math] = 4.64 W. Folglich ist der Wärmeleitwert gleich [math]G_W=\frac{I_W}{\Delta T}[/math] = 0.422 W/K.
- Box und Flasche (inkl. Wärmeübergänge) bilden bezüglich des Wärmeenergiestromes eine Serieschaltung von zwei Leitwerten. Geht man nun davon aus, dass die Leitwerte nicht vom Wärmestrom abhängen, teilen sie die Temperaturdifferenz zwischen aussen und innen (Eiswasser von 0°C) immer im gleichen Verhältnis. Zudem führt ein doppelt so grosses Temperaturgefälle zu einem doppelt so starken Wärmestrom.
- Der von aussen zufliessende Wärmeenergiestrom ist gleich [math]I_W=G_W\Delta T[/math] = 9.28 W. Dies ergibt am Ort des Eis-Wasser-Gemisches einen zufliessenden Entropiestrom der Stärke [math]I_S=\frac{I_W}{T_s}=\frac{9.28W}{273K}[/math] = 0.034 W/K. Um diesen Entropiestrom um 60 K hinauf zu pumpen, benötigt man eine Prozessleistung von [math]P=\Delta TI_S[/math] = 2.04 W.
Aufgabe 8
Das zu betrachtende System besteht aus nur einem Drehimpulsspeicher, dem Bohrkopf mit Bohrer. Vom Motor her fliesst ein konstanter Drehimpulsstrom zu. Der an das Werkstück weg fliessende Drehimpulsstrom wird in Abständen von fünf Sekunden ein- und ausgeschaltet.
- Das Flüssigkeitsbild besteht aus einem Topf, welcher für den Bohrkopf steht. Zum Zeitpunkt 2 s fliesst vom Motor her (Füllhöhe 419 1/s) ein Drehimpulsstrom der Stärke 20 Nm in den Topf (momentane Füllhöhe 293 1/s). Zum Zeitpunkt 6 s strömt immer noch Drehimpuls der Stärke 20 Nm zu. Zusätzlich fliesst noch ein Strom unbekannter Stärke weg. Die Füllhöhe beträgt nun 377 1/s.
- In 5 s fliessen 5 * 20 Nm = 100 Nms Drehimpuls zu. Gleichzeitig ändert sich die Winkelgeschwindigkeit um Δω = 209 1/s. Dies ergibt für das Massenträgheitsmoment einen Wert von [math]J=\frac{\Delta L}{\Delta \omega}[/math] = 0.478 kgm2.
- Aus der Drehimpulsbilanz [math]M_R-M_B=\dot L[/math] folgt [math]M_B=M_R-\dot L=M_R-\frac{\Delta L}{\Delta t}[/math] = 40 Nm.
- Die Prozessleistung ist gleich Stromstärke mal Potenzialdifferenz, als gleich Drehmoment mal Differenz der Winkelgeschwindigkeit
- PR = 20 Nm * 41.9 1/s = 838 W
- PB = 40 Nm * 377 1/s = 15.1 kW
Aufgabe 9
Das Bugrad hat am untersten Punkt eine Geschwindigkeit von [math]v=v_M-\omega r[/math] = 58 m/s nach rechts. Folglich wirkt die Gleitreibung nach links.
- Auf das Bugrad wirken die Gewichtskraft, eine Normalkraft sowie eine Gleitreibungskraft (nach links) ein.
- Die drei Bilanzgleichungen (Grundgesetze) lauten (x-Achse nach rechts, y-Achse nach unten, positive Drehrichtung im Uhrzeigersinn)
- x: [math]-F_R=\dot p_x=m\dot v_x[/math]
- y: [math]F_G-F_N=\dot p_y[/math]
- R: [math]F_Rr=\dot L=J\dot\omega[/math]
- In der Rutschphase sind die alle drei Bilanzgleichungen geometrisch entkoppelt. Deshalb können beide Fragen getrennt beantwortet werden
- [math]\dot v_x=-\frac{F_R}{m}=-\frac{\mu mg}{m}=-\mu g[/math] = -5.89 m/s2
- [math]\dot \omega=\frac{F_Rr}{J}=\frac{\mu mgr}{J}[/math] = 23.5 1/s
- Die Lösung zu dieser Teilaufgabe ist unter Bowling ausgiebig besprochen. Die entscheidende Idee lautet
- [math]\frac{F_Rr}{F_R}=\frac{|\Delta L|}{|\Delta p|}=\frac{J(\omega_e-\omega_a)}{m(v_a-v_e)}[/math] woraus folgt
- [math]v_e=\frac{mrv_a+J\omega_0}{\frac{J}{r}+mr}[/math] = 53 m/s