Atwoodsche Fallmaschine: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 10: | Zeile 10: | ||
==Herleitung== |
==Herleitung== |
||
Die [[Beschleunigung]], mit welcher sich der leichter Klotz nach oben und der schwerere nach unten in [[Bewegung]] setzt kann mit Hilfe der [[Energiebilanz|Energie-]] oder der [[Impulsbilanz]] berechnet werden |
|||
===Impulsbilanz=== |
===Impulsbilanz=== |
||
Zuerst [[freischneiden|schneidet]] man die beiden Körper frei und wählt die positive Bezugsrichtung längs der zu erwartenden Bewegung. Dann lautet die Impulsbilanz zusammen mit dem [[kapazitives Gesetz|kapazitiven Gesetz]] der Translationsmechanik (auch [[Grundgesetz der Mechanik]] genannt] |
|||
{| |
|||
|width="250"|Grundgesetz für den schweren Körper |
|||
|width="250"|<math>F_{G1}-F_1=m_1a_1</math> |
|||
|- |
|||
|Grundgesetz für den leichteren Körper |
|||
|<math>F_2-F_{G2}=m_2a_2</math> |
|||
|- |
|||
|kinematische Verknüpfung |
|||
|<math>a_1=a_2=a</math> |
|||
|- |
|||
|ideale Rolle und Seil |
|||
|<math>F_1=F_2</math> |
|||
|- |
|||
|Kraftgesetz der Gravitation |
|||
|<math>F_{G1}=m_1g</math> und <math>F_{G2}=m_2g</math> |
|||
|- |
|||
|Lösung |
|||
|<math>a=g\frac{m_1-m_2}{m_1+m_2}</math> |
|||
|} |
|||
Die Lösung für die idealisierte Maschine lässt sich auch erraten: die beiden Gewichtskräfte wirken gegeneinander und das Gesamtsystem besitzt eine Trägheit im Umfang der beiden (trägen) Massen. Die hier gezeigte, strukturierte Vorgehensweise erlaubt dagegen ein beliebiger Ausbau des Problems |
|||
*Rolle mit Trägheit: Grundgesetz der Rotation für die Rolle hinzufügen |
|||
*zwei verschiedene Wickelradien: kinematische Verknüpfung anpassen, Kräfte über [[Hebelgesetz]] berechnen |
|||
*Reibung: Grundgesetz der Rotation um Lagerreibung erweitern, Grundgesetze der Körper mit [[Luftwiderstand]] ergänzen |
|||
===Energiebilanz=== |
===Energiebilanz=== |
||
Version vom 13. August 2010, 17:24 Uhr
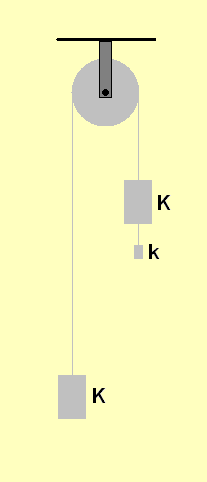
Die atwoodsche Fallmaschine wurde 1784 von George Atwood erfunden. Sie wurde als Nachweis für die gleichmässig beschleunigten Bewegung konzipiert. Mit ihr kann man die Fallbeschleunigung beliebig verringern.
Idealisierung
Die Fallmaschine wird meist sehr stark idealisiert
- Seil und Rolle ohne Masse
- Seil beliebig biegsam
- keine Lagerreibung
- kein Luftwiderstand
Herleitung
Die Beschleunigung, mit welcher sich der leichter Klotz nach oben und der schwerere nach unten in Bewegung setzt kann mit Hilfe der Energie- oder der Impulsbilanz berechnet werden
Impulsbilanz
Zuerst schneidet man die beiden Körper frei und wählt die positive Bezugsrichtung längs der zu erwartenden Bewegung. Dann lautet die Impulsbilanz zusammen mit dem kapazitiven Gesetz der Translationsmechanik (auch Grundgesetz der Mechanik genannt]
| Grundgesetz für den schweren Körper | [math]F_{G1}-F_1=m_1a_1[/math] |
| Grundgesetz für den leichteren Körper | [math]F_2-F_{G2}=m_2a_2[/math] |
| kinematische Verknüpfung | [math]a_1=a_2=a[/math] |
| ideale Rolle und Seil | [math]F_1=F_2[/math] |
| Kraftgesetz der Gravitation | [math]F_{G1}=m_1g[/math] und [math]F_{G2}=m_2g[/math] |
| Lösung | [math]a=g\frac{m_1-m_2}{m_1+m_2}[/math] |
Die Lösung für die idealisierte Maschine lässt sich auch erraten: die beiden Gewichtskräfte wirken gegeneinander und das Gesamtsystem besitzt eine Trägheit im Umfang der beiden (trägen) Massen. Die hier gezeigte, strukturierte Vorgehensweise erlaubt dagegen ein beliebiger Ausbau des Problems
- Rolle mit Trägheit: Grundgesetz der Rotation für die Rolle hinzufügen
- zwei verschiedene Wickelradien: kinematische Verknüpfung anpassen, Kräfte über Hebelgesetz berechnen
- Reibung: Grundgesetz der Rotation um Lagerreibung erweitern, Grundgesetze der Körper mit Luftwiderstand ergänzen