Carnotor

Der von Sadi Carnot eingeführte Zyklus wird heute noch dazu verwendet, den Begriff Entropie einzuführen. So genial die Idee damals war, so falsch ist heute der Versuch, mit diesem Gedankenexperiment Studierende zu traktieren, um ihnen ein Verständnis für die Entropie einzubleuen. Bald zweihundert Jahre nach der Veröffentlichung der grundlegenden Schrift von Carnot sollte man nicht mehr so tun, als ob die Entropie erst vor kurzem entdeckt worden sei. Will man die Zustandsänderungen des idealen Gases dennoch diskutieren und durchrechnen, kann man dies mit Hilfe des Carnotors tun. Der Carnotor ist eine virtuelle Maschine, die an der ZHW "erfunden" worden ist, um das Verhalten von Gasen mit Hilfe von systemdynamischen Werkzeugen zu modellieren.

ideales Gas

Das Modell des idealen Gases beschreibt den Zustand von stark verdünnten Stoffen, wobei die Wechselwirkung zwischen den Teilchen dieses Stoffes vernachlässigbar klein sein sollte. Sämtliche Gleichgewichtszustände des idealen Gases können mit Hilfe von zwei Zustandsgleichungen beschrieben werden.

Die thermische Zustandsgleichung oder das universelle Gasgesetz verknüpft vier Grössen, die Temperatur, den Druck, das Volumen und die Stoffmenge miteinander

[math]pV = nRT[/math]

Anstelle der kalorischen nimmt man als zweite Zustandsgleichung mit Vorteil die entropische. Sie beschreibt, wie die Entropie vom Volumen und der Temperatur abhängt

[math]S = S_0 + n (R ln \frac {V}{V_0} + \hat c_V ln \frac {T}{T_0})[/math]

Die Entropie nimmt logarithmisch mit dem Volumen und der Temperatur zu und ist proportional zur Stoffmenge. Auf ein Mol bezogen bildet die universelle Gaskonstante R den Proportionalitätsfaktor für den volumenmässige und die molare Wärmekapazität den Faktor für den thermischen Zuwachs.

Zweiport

thermische und mechanische Ports

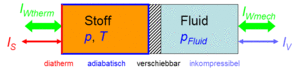
Der Zustand des idealen Gases kann auf zwei Arten verändert werden: durch heizen und kühlen oder durch komprimieren und entspannen. Um diese Prozesse kontrolliert ablaufen zu lassen, soll das Gas in einen Zylinder gebracht werden, der mit einem frei verschiebbaren Kolben abgeschlossen ist. Der Zylinderboden sei ideal wärmedurchlässig (diatherm), besitze aber selber keine Wärmekapazität. Die Zylinderwände und der Kolben sind absolut wärmeisoliert (adiabatisch). Der reibunsfrei verschiebbare Kolben schliesst das Gas hermetisch gegen eine inkompressible Flüssigkeit ab, welche für den Druckaufbau verantwortlich ist.

Das um die ideale Flüssigkeit erweiterte Gas besitzt zwei Ein-/Ausgänge (Ports). Über den thermischen Port wird Entropie und über den hydraulischen Volumen ausgetauscht. Die Volumen- und die Entropieströme sind je nach Druck und Temperatur mit Energie beladen (der Druck ist das hydraulische und die Temperatur das thermische Potenzial). Die vier grundlegenden Prozesse der Thermodynamik hängen nun nur noch von der Beschaltung der beiden Ports ab.

Prozess	thermischer Port	hydraulischer Port
isochor	aktiv	geschlossen
isobar	aktiv	offen
isotherm	offen	aktiv
isentrop	geschlossen	aktiv

Systemdynamisches Modell

Das Systemdiagramm des Carnotors

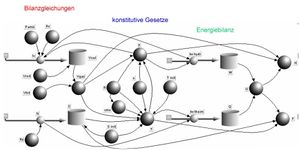
Das systemdynamische Modell geht von der Entropie- und der Volumenbilanz aus (bilanziert wird das Volumen der Flüssigkeit; das Volumen des Gases ist dann die Ergänzung zum Gesamtvolumen). Die beiden Potenziale, die Temperatur und der Druck, werden über die beiden Zustandsgleichungen ermittelt. Die Energie bildet wie überall in der Physik eine zweite Ebene. Aus den beiden zugeordneten Energieströmen werden die Wärme und die Arbeit integriert. Die Summe über die beiden Austauschformen ergibt dann die Änderung der inneren Energie. Die Enthalpie und die freie Energie werden a posteriori berechnet. .