Tut 2.1: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 2: | Zeile 2: | ||
==[[Radioaktiver Zerfall]]== |
==[[Radioaktiver Zerfall]]== |
||
Die meisten Elemente besitzen ein oder sogar mehrere [[Isotop]]e, die instabil sind und zu jedem Zeitpunkt mit einer bestimmten Wahrscheinlichkeit zerfallen. |
Die meisten Elemente besitzen ein oder sogar mehrere [[Isotop]]e, die instabil sind und zu jedem Zeitpunkt mit einer bestimmten Wahrscheinlichkeit zerfallen. Von einer gegebenen Anzahl von [[Atom]]kernen (''N'') eines [[Radioaktivität|radioaktiven]] Isotops zerfällt in jeder Sekunde ein gewisser Prozentsatz. Weil die Zerfallswahrscheinlichkeit gegeben ist, darf man behaupten, dass die Zerfallsrate proportional zur Zahl der noch vorhandenen Kerne ist |
||
:<math>\dot N = -\lambda N = -A</math> |
:<math>\dot N = -\lambda N = -A</math> |
||
[[Bild:Radioaktiver_Zerfall_SD.jpg|thumb|Systemdiagramm eines radioaktiven Zerfalls]] Der positiv genommen Wert der Zerfallsrate heisst Aktivität ''A'' und hat die Einheit Becquerel (Bq). Das [[System Dynamics|systemdynamische Modell eines radioaktiven Zerfalls ist äusserst einfach. Die Zahl der radioaktiven Atome bwz. der Atomkerne bildet die Bestandesgrösse und die Aktivität ist der einzige Abfluss. Das Bild zeigt das Systemdiagramm eines radioaktiven Zerfalls. |
[[Bild:Radioaktiver_Zerfall_SD.jpg|thumb|Systemdiagramm eines radioaktiven Zerfalls]] Der positiv genommen Wert der Zerfallsrate heisst Aktivität ''A'' und hat die Einheit Becquerel (Bq). Das [[System Dynamics|systemdynamische Modell]] eines radioaktiven Zerfalls ist äusserst einfach. Die Zahl der radioaktiven Atome bwz. der Atomkerne bildet die Bestandesgrösse und die Aktivität ist der einzige Abfluss. Das Bild zeigt das Systemdiagramm eines radioaktiven Zerfalls. |
||
Der radioaktive Zerfall kann statt über eine dynamische Modellierung auch mit Hilfe einer Funktion beschrieben werden. Integriert man die oben aufgeführte Beziehung über die Zeit, erhält man das Zerfallsgesetz |
|||
:<math>N = N_0 e^{-\lambda t} = N_0 e^{-t/\tau}</math> |
:<math>N = N_0 e^{-\lambda t} = N_0 e^{-t/\tau}</math> |
||
Die Zeitkonstante ''τ'' ist zur Zerfallskonstanten ''&lambda |
Die [[Zeitkonstante]] ''τ'' ist zur '''Zerfallskonstanten''' ''λ'' reziprok. Zerfallskonstante und Zeitkonstante lassen sich aus der [[Halbwertszeit]] berechnen |
||
:<math>\frac {N_0}{2} = N_0 e^{-\lambda t_{1/2}} = N_0 e^{-t_{1/2}/\tau}</math> |
|||
<math>\lambda = \frac {1}{\tau} = \frac {ln(2)}{t_{1/2}}</math> |
|||
'''Zürück zum [[Tutorial|Inhalt]] |
'''Zürück zum [[Tutorial|Inhalt]] |
||
Version vom 16. Juni 2007, 15:50 Uhr
Geordnete Strukturen oder komplexe Systeme haben die Tendenz zu zerfallen: alte Burgen verwittern und organisches Material wird durch Mikroben zersetzt, bis nur noch Wasser, Kohlendioxid und ein paar Salze vorhanden sind. Hinter den meisten Zerfällen steckt eine unpopuläre aber allmächtige Grösse, die Entropie oder der Wärmestoff. Die Entropie ist die einzige Grösse in der Natur, die produziert aber nie vernichtet werden kann.
Radioaktiver Zerfall
Die meisten Elemente besitzen ein oder sogar mehrere Isotope, die instabil sind und zu jedem Zeitpunkt mit einer bestimmten Wahrscheinlichkeit zerfallen. Von einer gegebenen Anzahl von Atomkernen (N) eines radioaktiven Isotops zerfällt in jeder Sekunde ein gewisser Prozentsatz. Weil die Zerfallswahrscheinlichkeit gegeben ist, darf man behaupten, dass die Zerfallsrate proportional zur Zahl der noch vorhandenen Kerne ist
- [math]\dot N = -\lambda N = -A[/math]
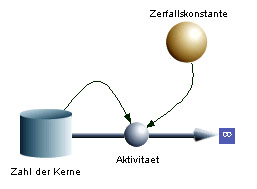
Der positiv genommen Wert der Zerfallsrate heisst Aktivität A und hat die Einheit Becquerel (Bq). Das systemdynamische Modell eines radioaktiven Zerfalls ist äusserst einfach. Die Zahl der radioaktiven Atome bwz. der Atomkerne bildet die Bestandesgrösse und die Aktivität ist der einzige Abfluss. Das Bild zeigt das Systemdiagramm eines radioaktiven Zerfalls.
Der radioaktive Zerfall kann statt über eine dynamische Modellierung auch mit Hilfe einer Funktion beschrieben werden. Integriert man die oben aufgeführte Beziehung über die Zeit, erhält man das Zerfallsgesetz
- [math]N = N_0 e^{-\lambda t} = N_0 e^{-t/\tau}[/math]
Die Zeitkonstante τ ist zur Zerfallskonstanten λ reziprok. Zerfallskonstante und Zeitkonstante lassen sich aus der Halbwertszeit berechnen
- [math]\frac {N_0}{2} = N_0 e^{-\lambda t_{1/2}} = N_0 e^{-t_{1/2}/\tau}[/math]
[math]\lambda = \frac {1}{\tau} = \frac {ln(2)}{t_{1/2}}[/math]
Zürück zum Inhalt